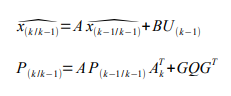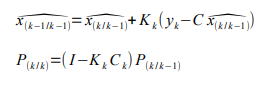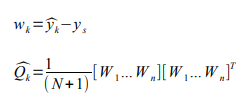IMA5 2018/2019 P24
Sommaire
- 1 Présentation générale
- 2 Préparation du projet
- 3 Réalisation du Projet
- 3.1 Journal de Bord
- 3.2 Description des concepts clés du filtrage de Kalman
- 3.3 Comment identifier le modèle du Robotino ?
- 3.4 Comment valider ce modèle ?
- 3.5 Filtrage de Kalman d'un système à étudier
- 3.6 Utilisation d'un signal sur mon premier modèle
- 3.7 Acquisition de mesures et commande
- 3.8 Mise en place de mon filtre sur le Robotino
- 3.9 Explication de la méthode pour la détection de défauts
- 4 Documents Rendus
Présentation générale
Description
Les observateurs sont généralement utilisés pour estimer des grandeurs mais en présence de bruits, leur performance se trouve dégradée. On a alors recours au filtrage de Kalman. Son application en diagnostic a permis la surveillance de plusieurs systèmes industriels. En effet, quand un défaut apparaît dans un système, il est crucial de le détecter tôt et de le corriger pour éviter sa propagation qui pourra endommager le système. Ce projet a pour but de mettre en œuvre un filtre de Kalman sur le robotino en vue de détecter l’apparition des défauts sur ce dernier. On commencera par apprendre et maîtriser le fonctionnement du filtrage de Kalman et la commande du Robotino avec Matlab. Suivra l’implémentation du filtre de Kalman pour la détection de défauts.
Le Robotino est un robot mobile omnidirectionnel, ainsi il est possible de le déplacer sur lui-même et dans toutes les positions voulues. A l'aide de sa webcam, il est possible d'observer ce que le robot observe en direct. Grâce à cette outil par exemple, il est intéressant de travailler sur une détection d'objet par exemple. Les différents capteurs du Robotino permettent de réaliser la mesure de distances, ces capteurs sont de type analogiques. De plus il est aussi composé de capteurs permettant d'éviter les différentes collision possibles durant un parcours par exemple. Il est aussi possible de contrôler les différents moteurs en envoyant une consigne à ceux-ci.
Concrètement, les modules des roues omnidirectionnelles sont composés d'un moteur à courant continu, un réducteur de rapport, une roue, une courroie crantée et d'un capteur incrémental. Ces 3 roues sont positionnés à 120 degrés les unes des autres.
La caméra peut être réglée au niveau de la hauteur et de l'inclinaison, il est alors possible de visualiser en direct ce que la caméra observe. A l'aide de la caméra, il est possible d'orienter des études sur le traitement d'images. Ce système est aussi capable de détecter les lignes par exemple, ce qui peut amener à travailler sur la localisation des objets ou le suivi de trajectoire.
Le module d'unité de commande est composé d'un point d'accès WLAN, d'une carte compact Flash de 256 Mo et d'un processeur PC 104 300 MHz.
Le Robotino est composé de différents capteurs, des capteurs infrarouges, de capteur anticollision, de capteur incrémental, et de capteur de proximité inductif analogique. Les capteurs infrarouges sont espacé de 40 degrés l'un de l'autre, il y en a donc 9, il est donc possible de les utiliser pour éviter les obstacles par exemple. Le capteur anticollission s'active lui à la moindre pression et peut par exemple s'arrêter lorsque celui-ci s'active. De plus le capteur incrémental permet de comparer la vitesse de consigne et la vitesse réelle. Ainsi, nous pouvons utiliser un régulateur PID pour arriver à la vitesse souhaitée. Alors que le capteur de proximité inductif analogique permet de détecter les différents objets métalliques sur le sol.
Objectifs
L'objectif principal de ce projet est la mise en œuvre un filtre de Kalman pour la surveillance d’un robot mobile. En effet, grâce à la mise en oeuvre de ce filtre de Kalman sur le Robotino qui est un robot mobile, il sera donc possible de détecter des défauts.
Préparation du projet
Cahier des charges
Choix techniques : matériel et logiciel
Lors de ce projet, les choix techniques sont les suivants :
- Un robot mobile : Le Robotino
- Le logiciel RobotinoView3
- Matlab Simulink
Liste des tâches à effectuer
Les tâches à effectuer sont les suivantes :
- Recherches bibliographiques et état de l'art
- Prise en main du Robotino
- Modélisation du système
- Recherches Filtre de Kalman
- Expérimentations sur les défauts
Calendrier prévisionnel
Voici les grandes étapes de mon projet de fin d'études. Celle-ci vont de la préparation du projet c'est-à-dire l'établissement du cahier des charges, les choix du matériel etc.. jusqu'à l'implémentation du filtre et la détection des défauts. Chaque semaine, un planning et des objectifs ont été proposé en réunion de projet pour bien mener le projet de bout en bout.
Réalisation du Projet
Journal de Bord
Semaine 1
Lors de cette première semaine, j'ai rencontré plusieurs fois mon tuteur de Projet, les points suivants ont été fixé :
- Organisation du PFE ==> Plusieurs réunions par semaine
- Travail préliminaire à réaliser
- Les notions à bien revoir
- Définition de l'objectif principal de ce projet
Semaine 2
Lors de cette semaine de travail, je me suis attardé sur les points suivants :
- Prise en main du Robotino
- Découverte et commande du Robotino à l'aide de Matlab
- Réalisation de parcours
- Recherche sur l'établissement du modèle du Robotino
- Recherche sur le filtre de Kalman
Semaine 3
Lors de ce début de semaine, la réalisation des tâches suivantes a été débuté :
- Recherches approfondies pour valider ce modèle
- Utilisation de techniques mathématiques pour valider ce modèle
Rencontre avec M. Pekpe en ce début de semaine les points qui se sont dégagés sont les suivants :
- Expositions de mes idées d'expérimentation
- Clarification sur certains points du projet
- Continuer de documenter mon travail
Semaine 4
En ce début de semaine 4, j'ai commencé les tâches suivantes :
- Travail su la méthode des résidus
- Rédaction de documents pour le fonctionnement de mes premières expérimentations
Semaine 5
Lors de cette semaine voici les tâches que j'ai continué et commencé :
- Travail sur la méthode des résidus
- Adaptation du modèle
- Travail sur le filtrage de Kalman, plus particulièrement sur un système plus simple
Semaine 6
Lors de cette semaine, le travail entamé est le suivant :
- Travail sur l'algorithme de Kalman
- Création d'un fichier pour initialiser la position du Robot avant l'utilisation de celui-ci
- Réalisation d'un filtrage de Kalman sur un signal sinusoïdal
Semaine 7
Lors de cette semaine, le travail principal sera le suivant :
- Calcul des paramètres pour le filtrage de Kalman sur le Robotino
- Test d'implémentation du filtrage
- Rédaction du rapport de projet
Une implémentation du filtre a été réalisé sur le Robotino, mais les sorties n'étant que simulées une erreur conséquente s'est installé dans ma prédiction. L'objectif de mes prochaines étapes est donc de ne plus avoir ce problème de bruit.
Semaine 8
Les différentes tâches à réaliser pour cette semaine sont les suivantes :
- Exploitation du bruit pour avoir un meilleur filtrage
- Travail avec la méthode des sous espaces pour pouvoir identifier la matrice de perturbation
- Une modification du modèle est donc à prévoir
La méthodologie et le travail actuel a été validé cette semaine avec M. Pekpe.
Semaine 9
Lors de cette semaine, je vais effectuer les tâches suivantes :
- Recherche d'une méthode pour pouvoir exploiter plus de paramètres
- Travail sur différents paramètres du robotino
- Cela implique un nouveau changement de mon modèle
- Mais aussi un changement de l'algorithme principal
- Rédaction du rapport de projet
Pour pouvoir mieux mettre en place la suite du travail, des étapes pour augmenter les nombres de sorties a été établi. De plus la méthodologie a été mise en place pour réaliser des tests supplémentaires sur la détection des défauts.
Semaine 10
Durant cette semaine, le travail s'orientera vers les tâches suivantes :
- Utilisation d'un seuillage et test de la méthode des résidus pour pouvoir analyser le système lorsqu'il n'y pas de défauts
- Travail sur une méthode pour pouvoir insérer des défauts que ce soit directement dans mes sorties ou plutôt en ajoutant un paramètre supplémentaire par exemple
- Réflexion pour essayer d'avoir un algorithme de Kalman encore plus précis
- Étude pour l'établissement d'une éventuelle amplitude pour la détection des défauts
- Rédaction du rapport de projet
Plusieurs acquisitions ont été réalisé pour pouvoir définir une zone plus précise. Ainsi, la focalisation sur cette zone plus précise permet d'évaluer le défaut sur l'un des capteurs par exemple.
Semaine 11
Lors de cette semaine de travail, la réalisation des tâches suivantes seront réalisées ou continuées :
- Acquisitions pour définir au mieux mes différents résidus
- Simulation d'un des défauts avec l'ajout d'un défaut sous la forme de biais
- Différencier les fonctionnement anormal par exemple si le Robotino s'éteint brusquement
- Rédaction du rapport de projet
Après avoir effectué une réunion avec M. Pekpe, il a été relevé qu'il fallait faire une nouvelles acquisitions plus longue car les données pouvaient être faussées lors de l'arrêt du Robotino pendant l'acquisition. Cela était donc problématique pour avoir un modèle encore plus précis. Un ajout de sorties dans mon modèle a aussi été envisagé pour que cela soit encore plus méthodique.
Lors de cette fin de semaine, et à l'aide de la prise en compte des conseils de M. Pekpe. Un modèle bien plus précis a été établi, de nombreux tests ont été réalisé cette semaine ainsi que la précédente. Le travail sur une méthode permettant d'ajouter des défauts directement dans une équations à aussi été établi durant cette semaine.
Semaine 12
Lors de cette semaine, les tâches suivantes seront réalisées, ou continuées :
- Finition des derniers tests et ajout de scénarios défauts
- Rédaction du rapport
- Préparation de la soutenance
Lors de cette semaine, la finition du projet a été réalisé.
Semaine 13
Lors de cette dernière semaine, le travail a été focalisé sur les tâches suivantes.
- Finalisation du rapport
- Préparation de la soutenance
Description des concepts clés du filtrage de Kalman
Le filtre de Kalman est un filtre à réponse impulsionnelle infinie c'est-à-dire que c'est un filtre qui se base sur les valeurs du signal d'entrée mais aussi des valeurs antérieurs de celui-ci. Le filtre de Kalman est donc une méthode permettant d'estimer les différents paramètres d'un système qui évolue dans le temps, tout cela à partir de mesures bruités. Le filtre de Kalman est donc utilisé dans de nombreux domaines tels que le traitement d'images, les radars...
Ce filtre est capable de prédire des paramètres du système, et de rectifier des erreurs. Grâce au filtre de Kalman, il est possible d'avoir des erreurs raisonnables et ainsi d'avoir des estimations correctes.
Il y a deux grandes étapes concernant le fonctionnement du filtre de Kalman :
- La première étape est la prédiction de l'estimation en fonction du modèle du système. De plus, dans cette étape, nous avons l'état prédit et l'estimation prédite de la covariance.
- La seconde étape vise à faire la mise à jour de cette prédiction à l'aide des nouvelles mesures. Alors que dans cette seconde étape, nous avons une équation d'innovation, la covariance de l'innovation, le gain de Kalman mis à jour, ainsi que l'état de mis à jour et la covariance de mis à jour. Finalement, l'objectif de cette seconde étape est d'avoir une estimation bien plus précise.
Pour l'utilisation du filtre de Kalman, le système doit être un système linéaire bruité. Nous pouvons écrire sous la forme suivante le système :
Rappel sur les bruits blancs Gaussiens : Un bruit blanc est un processus aléatoire ayant la même densité spectrale de puissance(DSP) à toutes les fréquences de la bande passante. On dit qu'un bruit blanc est Gaussien lorsqu'il a une distribution normale et que sa moyenne est nulle. De plus ce bruit est ajouté au système. Pour commencer, nous savons que nous avons besoin de mesures pour le filtre de Kalman et étant donné que nous n'en avons pas au début il faut bien initialiser une valeur. Nous recherchons à minimiser la matrice de covariance de l'erreur.
Par la suite les deux étapes nécessaires au fonctionnement de ce filtrage sont la prédiction et la correction.
- Étape de prédiction :
Lors de l'étape de prédiction, nous avons l'erreur d'estimation qui croit car l'initialisation était obligatoire pour la suite et le bon fonctionnement de l'algorithme.
- Étape de correction :
Nous prenons en compte les différentes mesures pour corriger l'estimation trouvée. C'est pour cela que nous utilisons le théorème récursif des moindres carrés.
Comment identifier le modèle du Robotino ?
L’identification est la détermination du modèle d’un système sous forme de représentation d’état de manière numérique à partir des mesures d’entrée et de sorties. Concernant l'identification du modèle, nous utilisons la méthode des sous espaces. On considère le système linéaire à temps invariant suivant :
X(k+1) = AX(k) + BU(k) Y(k) = CX(k) + DU(k)
A, B, C et D sont les paramètres du système. X(k) appartient R^n représente l'état du système. U(k) appartient R^m représente l'entrée du système. Y(k) appartient R^m représente la sortie du système.
A l'aide de ce modèle, il faut rechercher une équivalence permettant d'avoir les matrices A, B, C, D. Nous déduisons que la réalisation équivalente peut être la suivante :
X(k+i) = A^i*X(k) + [A^(i-1)*B|A^(i-2)*B|...|AB|B]*[U(k), U(k+1), ..., U(k+i-2), U(k+i-1)] /H(i) = [A^(i-1)*B|A^(i-2)*B|...|AB|B] et /U(k) = [U(k), U(k+1), ..., U(k+i-2), U(k+i-1)]
Nous obtenons alors des estimations des matrices d'observabilité étendue et de séquences permettant finalement, l'obtention du système suivant :
[Valeur estimée de X(k+1), /Yk] = [A;B , C;D] * [Valeur estimée de X(k), U(k)]
Comment valider ce modèle ?
Concernant la validation du modèle, il faut utiliser la méthode des moindres carrées. La méthode des moindres carrés permet de sélectionner parmi ces fonctions celle qui reproduit le mieux les données expérimentales. On parle dans ce cas d’ajustement par la méthode des moindres carrés. La formule de cette méthode est la suivante :
Sum(t)(yest - y)²
err =-------------------
Sum(t)y²
err est l'erreur entre le modèle estimé et le modèle réel yest est la valeur d'un modèle estimé sur une période t y est la valeur d'un modèle réel sur une période t
Filtrage de Kalman d'un système à étudier
Pour commencer, j'ai choisi un système discret pour pouvoir le simuler, j'ai réalisé des simulations en régime permanent et à temps invariant. Dans ce cas, un bruit sera ajouté car dans la simulation, si nous n'avons pas de bruit le résultat s'éloignera fortement de la réalité. Le système choisi est régi par les matrices suivantes qui représentent la dynamique du système simulé. Les matrices A, B, C et D sont donc les suivantes :
A = [3.1587 2.7410 -0.8520;
1.4412 6.6666 0;
0 8.8888 2.2541];
B = [0.5487;
7.4587;
-2.2587];
C = [1 0 0];
D = 0;
Dans ce cas l'utilisation des équations du filtre de Kalman sont nécessaires, j'ai utilisé les équations de mise à jour du temps ainsi que celle de la mise à jour des mesures. Dans mes différentes équations, je tiens compte des mesures passées pour prédire l'état futur lors de la mise à jour. En effet, la correction sera réalisé en fonction de l'équation d'innovation c'est-à-dire que l'écart que nous trouvons entre les différentes valeurs mesurées et les différentes valeurs prédites. Ainsi, cet écart est le gain d'innovation, celui-ci permet de minimiser la covariance en tenant compte du bruit. De cette manière nous pourrons estimer à l'aide de ce filtre une estimation optimale de notre sortie.
Dans mon cas, j'ai ajouté un bruit qui correspondrait au bruit du Robotino. L'ajout de ce bruit dans mes équations d'état était donc nécessaire pour avoir une simulation utile. J'ai donc un modèle discret, et choisi au préalable des valeurs pour les coefficients des bruits des capteurs et le bruit du système. Après avoir crée mon système, tous les paramètres de mon modèle sont déterminés. L'objectif de cette simulation est donc de pouvoir comparer la sortie du filtre de Kalman et la sortie réelle. Mais afin d'avoir une simulation exploitable, il fut intéressant de faire des comparaisons avec plus ou moins de bruit. Dans mon système, j'ai mis mon filtre de Kalman dans un retour. L'étape suivante était l'implémentation d'un signal quelconque, (utilisation de fonction affines, fonction cosinus etc...) dans ce cas, j'ai utilisé la fonction cos.
La comparaison avec la sortie filtrée et la sortie réelle a donc été logique. Grâce au différentes mesures de l'erreur de covariance, nous pouvons constater que celle-ci à été réduite de deux après le filtrage à l'aide du filtre de Kalman.
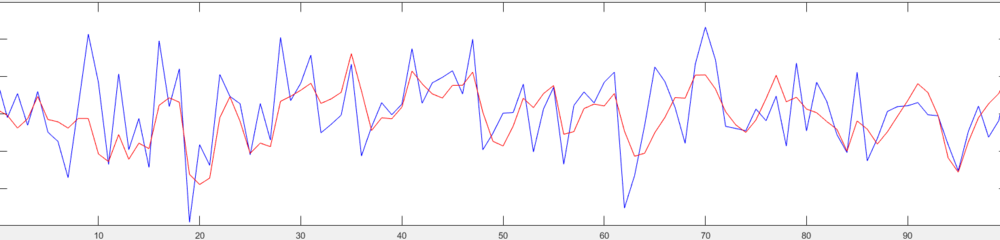
Concernant le filtrage de kalman variant dans le temps, j'ai réutilisé une partie du filtrage de Kalman en régime permanent. Cette fois, le covariance du bruit était aussi variante. L'ajout de récursivité pour pouvoir travailler dans le temps a donc été fortement utile. Dans ce cas, les matrices d'estimation d'état et de covariance d'erreur sont mise à jour à chaque itération. L'utilisation des bruits est nécessaires pour les mêmes raisons que précédemment. Après avoir implémenté le nouvel algorithme, la comparaison entre la sortie réelle et la sortie estimée a été réalisé.
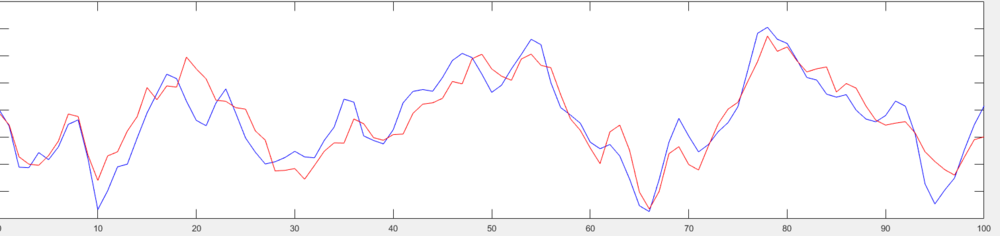
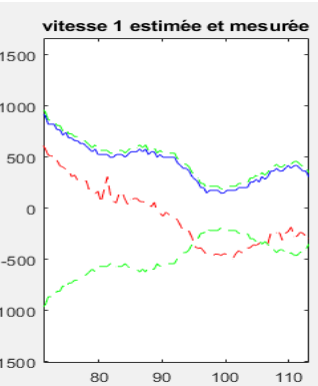
Ce premier graphique montre la réponse de la sortie réelle en bleu et la réponse du filtrage de Kalman en rouge.
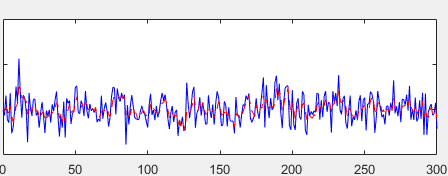
Ce second graphique nous montre l'erreur de la mesure et l'erreur du filtrage. De plus en régime à temps variant nous avons une erreur de covariance inférieure à la valeur théorique. En effet la covariance de sortie atteint un état stable à partir de la huitième itération. Par contre, la matrice de gain ne change pas par rapport au régime permanent.
Utilisation d'un signal sur mon premier modèle
Pour pouvoir obtenir les différents paramètres de mon premier modèle, j'ai utilisé la méthode des sous espaces. Ainsi, à l'aide de cette méthode j'ai pu identifier les paramètres de mes différentes matrices A, B, C, D. Avant d'obtenir ces différents paramètres, il était nécessaire d'effectuer des acquisitions de données à l'aide du Robotino. Une fois ces paramètres obtenus, je les utilise pour mon filtrage de Kalman. Il ne faut pas oublier que dans ce nouveau cas, le bruit est ajouté dans l'algorithme. Dans cette simulation, seulement les paramètres du Robotino ont été intégré.
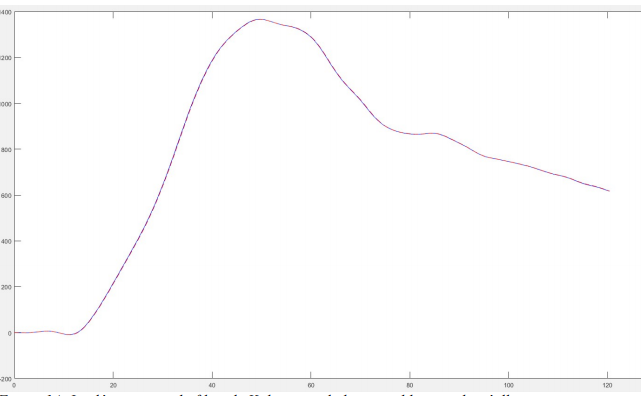
Ainsi, avec ce premier modèle, l'observation principale des résultats amène à conclure que l'établissement de ce premier modèle n'était pas correct car l'erreur était assez grande et donc nous avions un estimation assez éloignée de ce que nous voulions. Cela était aussi du à l'erreur de la matrice de variance - covariance. Les résultats étaient tout de même positifs, le fonctionnement de l'algorithme à l'aide des paramètres est donc fonctionnel.
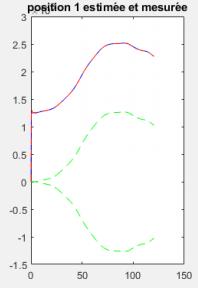
Cette courbe permet de visualiser et de mieux comprendre les différentes explications données précédemment. Dans cette partie, le signal utilisée n'était pas encore le signal de la commande du Robotino. Le signal était le même que dans l'explication du précédent cas, en effet dans une des prochaines partie l'explication avec le filtrage de Kalman en ligne sera réalisée.
Acquisition de mesures et commande
L'étape qui précède l'identification et la validation du modèle est la collecte de données. Ainsi pour cela l'établissement d'un parcours a été effectué, cette partie fut alors la partie commande. Le parcours a été établi pour durer assez longtemps c'est-à-dire entre 45 min et 1 heure. Ensuite, dans cet enregistrement de données nous avons les différentes données concernant les moteurs par exemple. Au départ le lacet du robot nous intéressé particulièrement. Les entrées du système sont les consignes de vitesses angulaires envoyées et la sortie était le lacet du robot mobile. Le Robotino était testé sur la piste de test de robots de Polytech Lille.
Mise en place de mon filtre sur le Robotino
Pour commencer, il faut savoir qu'il faut mettre la toolbox pour le Robotino si celle-ci n'est pas déjà mise. Il est donc préférable de toujours entrer les commandes suivantes si l'on change souvent de PC :
addpath( strcat( getenv('ROBOTINOMATLAB_DIR'), '/blockset' ) );
addpath( strcat( getenv('ROBOTINOMATLAB_DIR'), '/toolbox' ) );
Nous construisons ensuite les objets que nous allons utiliser dans notre programme. Nous avons besoin du ComId pour pouvoir ensuite se connecter au Robotino, puis du Bumper pour pouvoir s'arrêter en cas de collition, de l'OmniDrive, de l'Odometry et des différents moteurs où nous assimilant leur numéros de moteur.
Nous devons ensuite configurer le Robotino puis nous nous connectons sur celui-ci. De plus, après notre connexion au Robotino, nous chargeons les documents de commande et le modèle du Robotino.
Ensuite dans mon cas, j'envoie une consigne pour chaque roues du robot à trois roues omnidirectionnelles. Il est donc possible de les observer en temps réel et de les comparer avec la consigne envoyée au préalable.
Modifications paramétriques majeures du modèle
Pour identifier les différents paramètres du Robotino, nous utilisons la méthode des sousespaces décrite précédemment. En utilisant cette méthode à partir de mesures nous obtenons les différentes matrices A, B, C et D mais pour avoir une filtre de Kalman performant l'un des changements majeurs fut l'identification des paramètres G, R et Q. Ainsi en trouvant G nous aurons une initialisation beaucoup plus proche de la réalité. Pour trouver la matrice G nous pouvons aussi utiliser la méthode des sous-espaces. Dans ce cas, nous pouvons constater que K équivaut à notre G il est donc faisable de trouver son approximation. De plus pour trouver les paramètres R et Q il a fallu étudier le bruit que nous avions entre la sortie réel et la sortie estimée. Ceci nous a amené à en déduire par exemple que Q équivalait à :
Pour réaliser des études de bruits, il a donc été nécessaire de faire le calcul de la sortie estimée du filtre de Kalman avec la sortie réelle du Robotino. De plus dans un premier temps il a été plus simple de trouver l'équivalence de R en faisant l'hypothèse que le bruit de mesure était le même.
Concernant l'implémentation du filtre sur le modèle complet, le principe était le même que précédemment. Dès le départ le but était de l'implémenter sur la position du lacet. Au départ nous avions une grosse différence entre la sortie estimée et la sortie réelle. De plus comme nous pouvons le remarquer sur la figure 14 ces deux courbes sont confondus. La performance du filtre de Kalman est donc réelle, pour information ce modèle a été identifié et validé.
Explication de la méthode pour la détection de défauts
Changements réalisé sur le système avant la détection de défauts
L’objectif est de pouvoir utiliser le filtre de Kalman sur plus de sorties car nous n'avons pour l'instant que l'utilisation du filtre de Kalman sur le lacet. Le Robotino possède trois entrées à savoir les vitesses qu’on donne comme consigne, et nous avons qu'une seule sortie qui est la position du lacet. Cependant l'objectif suivant, a pour but de considérer d’autres sorties comme, les vitesses angulaires des roues, les positions x et y.
- Dans un premier temps, le choix des sorties seraient les vitesses angulaires des roues, ainsi que les différentes positions des roues.
- Nous pouvons ensuite faire une acquisition assez longue pour pouvoir enregistrer les différents bruits pour chaque sortie.
Remarque : Possibilité de rajouter plus d'itérations pour que le filtre soit plus précis.
- Après cette acquisition il suffira de mettre dans un fichier pour identifier le modèle pour pouvoir le valider par la suite.
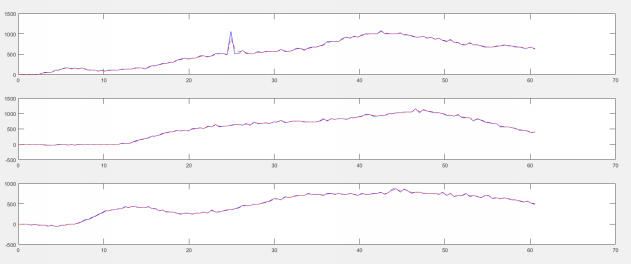
En suivant les précédentes manœuvres, nous pourrons utiliser le filtre de Kalman de manière optimale. De plus, pour pouvoir obtenir les différentes vitesses des roues la séparation de la matrice est nécessaire. Après avoir réalisé la séparation de ces matrices pour avoir les vitesses angulaires de chaque roue ainsi que les positions nous incluons le filtrage de Kalman pour ces différentes sorties et nous obtenons cela. Cette méthode fut la première utilisée, par la suite, un changement a été réalisé dans la sortie du modèle pour avoir une meilleure estimation.
Surveillance et détection de défaut
Il est nécessaire de réaliser de la surveillance sur un système, pour détecter les différents défauts d'un système. Nous pouvons définir le mode de fonctionnement à partir des données que nousavons collecté précédemment. Pour réaliser des diagnostics, nous pouvons utiliser des données en ligne et hors ligne.
Un défaut existe une fois que nous avons un écart avec la valeur théorique et la valeur mesurée. Lorsqu'il n'y a pas de défauts l'erreur est quasiment nulle, en effet les défauts peuvent arriver au niveau des actionneurs et au niveau des capteurs.
Résidus
Pour détecter les défauts, l'utilisation de résidus a été réalisé. Les résidus sont mis en place à l'aide des mesures réalisées et des calculs théoriques. Dans un premier temps, l'établissement de résidus fixes a été effectué. Puis dans un second temps, les résidus ont été implémenté pour évoluer pendant la période demandée. Une fois cela effectué nous pouvons décider s'il y a un dysfonctionnement ou non.
Après cela, une modification d'un élément d'une de ces matrices m'a permis d'inclure un défaut. Ainsi j'ai donc fait plusieurs scénarios pour pouvoir tester des visualisations de défauts.
Ensuite, après divers tests, j'ai pu décider des différentes valeurs de mes seuillage pour
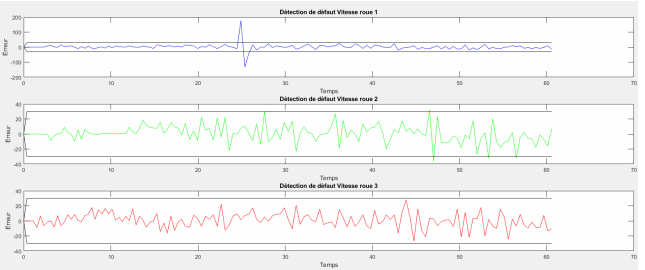
pouvoir dire s'il y avait défaut ou non. Comme nous pouvons l'observer, je
n'ai ajouté qu'un défaut au niveau de la vitesse angulaire de la première roue. Et nous
voyons bien que ce défaut et bien visible car il dépasse bien notre seuillage
Par contre nous pouvons remarquer qu'au niveau des positions rien n'a changé et cela est
normal car il n'y a pas de défauts.
Résidus évolutifs :
Concernant les résidus évolutifs, une matrice a été crée pour pouvoir avoir des résidus qui évoluent bien en fonction de la valeur réel. De plus, un calcul a été réalisé pour cela en effet après avoir réalisé le calcul de la sortie réelle et de la sortie estimée. Nous calculons la covariance de cela pour ne récupérer que les écarts types de ces matrices. Ensuite la création d'un matrice comportant la racine carrée de ces valeurs est établie. Dans cette exemple j'ai mis une matrice 6x6 mais celle-ci peut différer en fonction des sorties. Lorsque cela a été réalisé, nous mettons cette enveloppe de résidus à plus ou moins trois fois l'écart type.
On ajoute un défaut et pouvons observer directement les écarts :