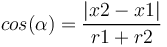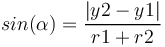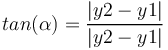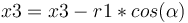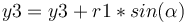IMA5 2022/2023 P20

Présentation générale

Contexte

En 2015 des étudiants de la filière IMA de Polytech ont réalisé une table connectée comportant un écran tactile pour leur projet de fin d'études. Cette table est aujourd'hui inexploitée.

Objectifs

L'objectif de ce projet est donc de créer un jeu de billard en réalité augmentée en profitant des caractéristiques de la table. En plus d'offrir une expérience unique grâce à une caméra qui permet de jouer avec une queue adaptée similaire à celle d'un véritable billard. Il sera également possible de suivre les parties grâce à une application mobile sur un appareil connecté en Bluetooth à la table.

Historique

Ce projet sera le deuxième projet réalisé sur cette table connectée, après la réalisation en 2018 d'une table de bar connectée par des étudiants en IMA de Polytech Lille. [1] La réalisation de la table de billard a été fait par sur ce wiki [2]

Cahier des charges

Fichier:P20 2022 2023 cahier des charges.pdf

Cahier des spécifications

Fichier:P20 2022 2023 cahier des spec.pdf

Diagramme de Gantt prévisionnel

Mathématiques générale liée au billard

Calcul de collision entre deux balles

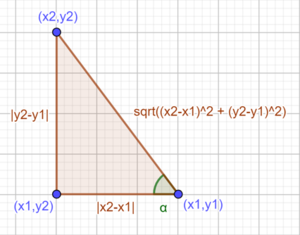
Il faut calculer si deux balles sont en collision, il existe une façon simple de calculer cette collision. Soit deux objets circulaire :

• C1 de centre (x1,y1) et de rayon r1
• C2 de centre (x2,y2) et de rayon r2

Si on imagine une ligne entre les deux centres des cercles, la distance D qui sépare les deux centres est :

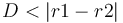• $D < |r1-r2|$ si les deux boules sont en collision
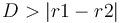• $D > |r1-r2|$ si les deux boules ne sont pas en collision

Pour faire l'algorithme de collision, il suffit de vérifier que : $(x2-x1)^2 + (y2-y1)^2 <= (r1+r2)^2$

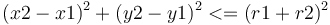
Il est aussi possible de calculer l'angle α à partir de formules basique de trigonométrie :

• $cos(\alpha )=\frac{|x2-x1|}{r1+r2}$
• $sin(\alpha )=\frac{|y2-y1|}{r1+r2}$
• $tan(\alpha )=\frac{|y2-y1|}{|y2-y1|}$

Et éventuellement le point de collision (x3,y3) :

• $x3 = x3 - r1*cos(\alpha )$
• $y3 = y3 + r1*sin(\alpha )$

Travail hebdomadaire réalisé

Semaine 1 (05/09/2022 - 09/09/2022)

• Réalisation du cahier des charges
• Ébauche d'un diagramme de Gantt prévisionnel en début de projet