Etude des possibilités de distribution d'un algorithme de surveilance

Introduction

Dans le cadre de notre formation en dernière année IMA, nous avons été amenées à effectuer un projet de fin d'études. Vu l'importance de ce dernier dans le cadre de notre projet professionnel, notre choix s'est porté sur l'étude des possibilités de distribution d'un algorithme de surveillance car nous sommes toutes les deux intéressées par la supervision, le diagnostic, la tolérance aux fautes et la surveillance des systèmes automatisés, sujets qui sont au coeur des préoccupations industrielles courantes. Ce projet nous initiera également à la maîtrise d'outils de développement industriel pour résoudre des problématiques courantes, à savoir la détéction, l'isolation des défauts et le contrôle/commande distribué. D'où l'intérêt porté sur celui-ci.

Présentation du projet

Les systèmes automatisés sont de moins en moins contrôlés et supervisés de façon globale. Leur architecture évolue d’une architecture centralisée vers une architecture distribuée où les algorithmes de commande sont implantés au plus près des producteurs d’informations. Les capteurs et actionneurs deviennent des instruments intelligents capables de prendre en compte des fonctions habituellement implantées à un niveau global de supervision. L’objectif du projet est d’étudier les possibilités de distribution d’une application de surveillance (détection et localisation de défauts) en partant d’une architecture distribuée définie uniquement du point de vue commande. Pour ceci, le projet se découpera selon les grandes parties suivantes : - Etude de l’analyse structurelle, approche classiquement utilisée pour générer des relations de redondance analytique, permettant d’élaborer des algorithmes de surveillance. - Proposition d’une démarche pour répartir au mieux les algorithmes de surveillance au plus près des producteurs d’informations. - Validation de la démarche proposée sur le générateur de vapeur. Cet équipement, installé en D301, reproduit le fonctionnement d'une centrale thermique. Il sert de support à la validation de travaux de recherche dans le domaine de la supervision des systèmes automatisés (détection et localisation de défauts, élaboration de lois de commande tolérantes aux fautes …). Les algorithmes sont développés sous Matlab/Simulink et implantés sur une carte d’acquisition et de traitement temps réel DSPACE.

Dans un premier lieu, nous allons donc comprendre le principe de l'analyse structurelle pour l'étudier sous le générateur de vapeur. Ensuite, nous allons proposer un algorithme de surveillance afin de décentraliser la commande des différents systèmes du générateur de vapeur, pour au final l'implémenter sous la carte DSPACE.

Réalisations

Du 17 septembre au 29 septembre Documentation sur l'analyse structurelle

Documents :

• Analyse_Structurelle_Staroswiecki.pdf
• Diagnosis and default tolerant control

Résultats :

• Compréhension du principe de l'analyse structurelle, en parallèle avec le cours de Supervision (Mr. Bouamama)
• Rédaction d'un premier rapport intermédiaire expliquant le principe des relations de redondances analytiques, des matrices de signatures des fautes, et du couplage.

Du 1er octobre au 15 octobre

Documentation sur le générateur de vapeur (GV)

Documents :

• HERMES_GV_FINAL.pdf
• GV_MARCEL.pdf

Résultats :

• Interprétation de l'analyse structurelle sur le GV
• Création des RRA du GV, de la Matrice de signature des défauts. (MSF)

Du 15 octobre au 20 octobre

Documentation sur La MSF des étudiants de l'année dernière Comparaison avec notre MSF obtenue

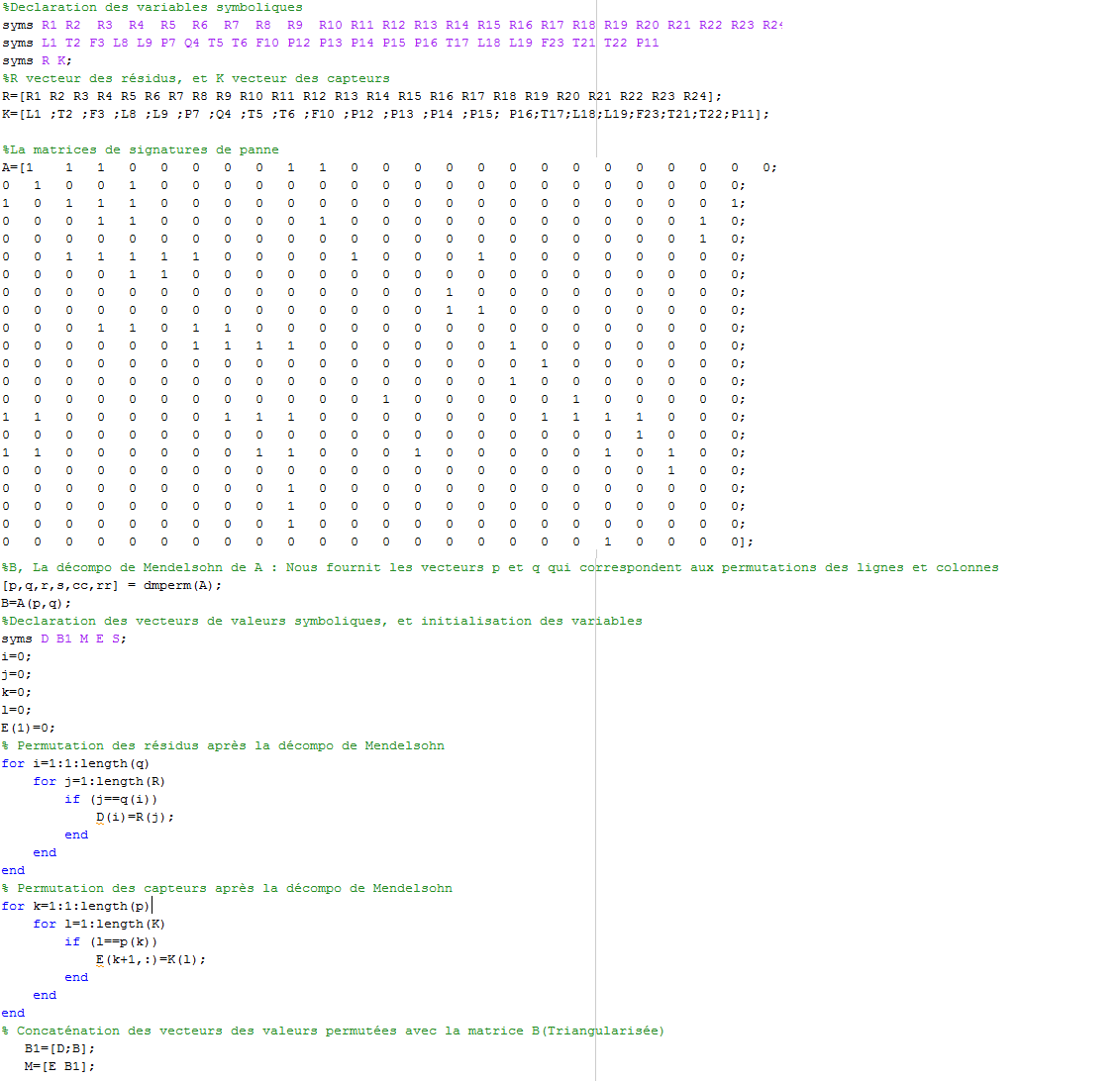
Du 5 novembre au 17 novembre Implémentation d'un algorithme Matlab, avec la fonction de Dulmage Mendelsohn, pour obtenir une MSF triangulaire supérieure afin de faciliter sa décomposition en sous-systèmes. Résultats :

• Voir code pièce jointe :

La matrice résultante après la décomposition de Mendelsohn est la suivante :

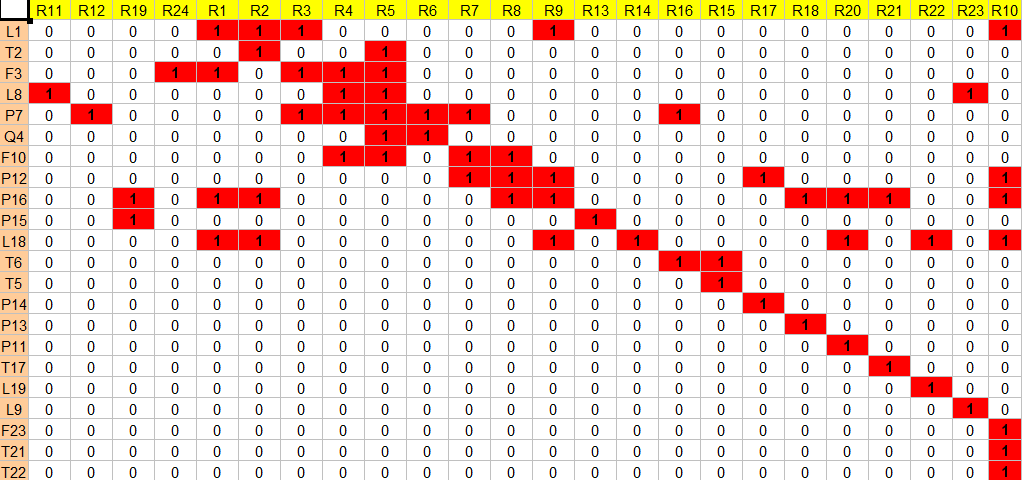
Notons que la décomposition de Mendelsohn n'est pas unique, mais nous fournit plusieurs décompositions pas plus triangulaires que celle obtenue. Ainsi, la matrice obtenue nous facilite la décomposition en sous-systèmes.

Notons également que nous pouvons procéder manuellement à cette décomposition en sous-systèmes, mais cette méthode a été déjà effectuée l'année passée, et nécessite l'étude de chaque cas à part. D'où la nécessité de créer un algorithme qui nous effectue la décomposition automatique quelque soit la matrice et le système étudié.

Du 20 novembre au 24 novembre

Prise en main du GV et des capteurs installés Rédaction d'un 2nd rapport intermédiaire, résumé de ce qui a été fait.

Photo du GV :

Du 26 novembre au 1er Décembre

But : Création d'un premier algorithme de décomposition sous Matlab, pour la décomposition en sous-systèmes, dans le but de décentraliser la commande du GV.

Il existe déjà 4 microcontrolleurs, et un PC maître qui les supervise, il faudra donc séparer le système en 4 sous-systèmes, appelés aussi unité de contrôles (CU).

Les CU doivent être décomposés de façon à réduire les flux sur le bus de terrain les reliant entre eux. Il faudra donc réfléchir à une procédure qui minimise ce flux, en introduisant à partir de la MSF, les différents capteurs et le calcul des RRA dans les 4 CU.

Du 3 décembre au 13 décembre

Résultat du 1er algorithme non satisfaisant, recherche d'un deuxième algorithme répartissant la matrice sous 3 sous-systèmes, se basant sur l'algo suivant :

Soit A la matrice de signature Pour i allant de 2 à la taille A Faire Pour j allant de 2 à la taille de A Faire ***** la somme des colonnes ***** N <-- la somme de A(i,j) ***** la somme des lignes ***** S <-- la somme de A(j,i) Fin Pour Fin Pour

Pour k allant de 2 à la taille de N Faire Si N(k) = min (N) Alors On mémorise K dans mem_k Fin Si Fin Pour

Pour l allant de 1 à la taille de mem_k Faire Pour m allant de 2 à la taille de A Faire Si A(mem_k(l),m)= 1 Si oui on regarde si S(m) = min (S) on memorise la ligne mem_k(l) de A dans mem_li on memorise la colonne m de A dans mem_co Fin Si Fin Si Fin Pour Fin Pour

-on concatene la ligne A(mem_li,:) avec la matrice A -A= [A(mem_li A] -on supprime A(mem_li,:) de A -on concatene la colonne A(:,mem_co) avec la matrice A -A=[A(mem_co; A] -on supprime A(:,mem_co) de A -on répéte la même demarche: la somme des colonnes sans compter la colonne déjà concatenée avec A la somme des lignes sans compter la ligne déjà concatenée avec A on cherche le min dans N et S cette fois-ci entre les min(N), on privilège les lignes qui ont des élements en commun avec la colonne de l'étape précedente

-Jusqu'à l'obtention d'une matrice triangulaire.

cet algorithme nous permet d'avoir un résultat satisfaisant, comme l'illustre la figu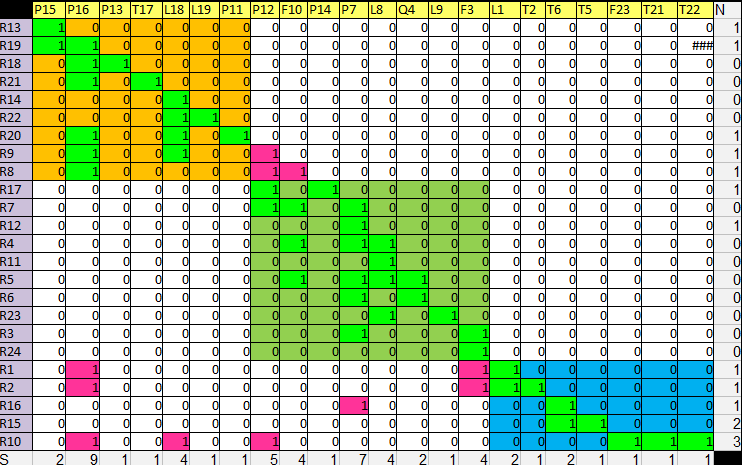re Nous avons validé la démarche par la prof. Nous avons également rédigé le rapport et le PPT pour la soutenance du mardi 18 dédembre.