RoboCup 2015 - Pyro Team

Cahier des charges

Présentation générale du projet

Avec plusieurs IMAs, nous avons créer une équipe pour participer à la Logistic League de la RoboCup. Lors de la compétition de l'Open German, version européenne de la RoboCup, il faudra mettre en place un système autonome de production à l'aide de Robotinos (robots mobiles de Festo ayant un système d'exploitation Linux) afin de réaliser des produits en fonction des demandes de l'arbitre du jeu : la Referee Box. Nous traiterons dans ce projet de l'aspect navigation des robots, composé d'une partie localisation et d'une partie déplacement.

Contexte

La compétition de l'Open German se déroule en quatre phases spécifiques : phase de début-de-jeu, phase d'exploration, phase de production, phase de fin-de-jeu. La navigation sera utilisée dans la phase d'exploration afin de réaliser une carte de la zone de jeu permettant de définir des zones de passage entre les machines. Dans la phase de production, la navigation permettra de se déplacer à partir de la carte créée au préalable (avec les obstacles fixes) et des robots (obstacles mobiles) se déplaçant en même temps.

Objectif du projet

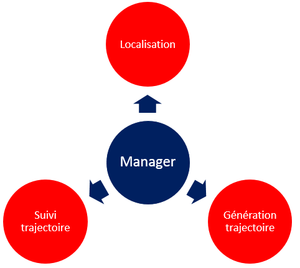
Fournir aux Robotinos un système capable de se localiser et de parcourir des trajectoires calculées à partir de coordonnées envoyées par le Manager.

Description du projet

• Localiser correctement le robot (à 5 cm près)
• Localiser les éléments fixes :
  • Murs
  • Machines
• Générer une trajectoire selon :
  • les demandes du "Manager"
  • la détection d'obstacles dynamiques (robots)
• Assurer le suivi de la trajectoire

Choix techniques : matériel et logiciel

• Utilisation de 3 Robotinos équipés chacun de :
  • 1 détecteur laser pouvant réaliser des mesures à 240°
  • 1 gyroscope
  • 9 capteurs SHARP (télémètres infrarouges)
  • 3 codeurs incrémentaux présents en sortie de chaque moteur du Robotino
• Utilisation de ROS Hydro
• Utilisation de différents langages : C++ ou Python
• Utilisation de Linux Ubuntu 12.04

Etapes du projet

• Conception du schéma global des différentes parties :
  • Localisation avec le SLAM
  • Création de la carte avec le SLAM
  • Génération de trajectoire avec A-Star
  • Execution de trajectoire avec le noeud ROS pour Robotino robotino_local_move

• Codage des différents noeuds ROS

• Tests de précision et de robustesse sur robot

• Validation du modèle

• Améliorations possibles :
  • Fusionner les maps des 3 robots
  • D-Star Lite au lieu de A-Star
  • Filtrage des données laser

Vocabulaire

Nos comptes rendus peuvent contenir des expressions que nous employons régulièrement mais qui ne sont parfois pas évidentes. Nous proposons alors cette partie vocabulaire afin d'aider le lecteur à comprendre ces expressions.

• Noeud : C'est un programme qui tourne de manière indépendante et qui réalise une tâche spécifique.

• Type : C'est un format spécifique de message. Il définit les valeurs que peut prendre une donnée, ainsi que les opérateurs qui peuvent lui être appliqués.

• Odométrie : L’odométrie est une technique permettant d'estimer la position d'un véhicule en mouvement. Cette mesure de bas niveau est présente sur quasiment tous les robots mobiles, grâce à des capteurs embarqués permettant de mesurer le déplacement du robot (de ses roues).

Avancement du Projet

Semaine 1

• Participation aux Finales Nationales des Olympiades des Métiers en robotique mobile (4ème)

Semaine 2

Etablissement du cahier des charges

• Prise de connaissance des contraintes d'environnement
• Dialogue avec l'équipe responsable de la partie Manager

Familiarisation avec l'environnement logiciel ROS Recherches de solutions pour la localisation (SLAM) et la génération de trajectoire (algorithme A-star)

Recherche d'un algorithme de recherche de chemin

Nous avons fait nos recherches en nous orientant sur le déplacement du Robotino afin de trouver un algorithme de recherche de chemin, capable de trouver le chemin le plus court, puisqu'un des buts de la compétition étant la rapidité.
Plusieurs algorithmes sont donc ressortis :

• L'algorithme Dijkstra (On part du point de départ et on cherche le chemin le plus court vers le point d'arrivée en cherchant dans TOUTES les directions)
  
• L'algorithme A-Star (Basé sur Dijkstra, cet algo s'oriente directement vers le point d'arrivée en minimisant la distance avec celui-ci)
  
• L'algorithme D-Star Lite (Amélioration du A-Star avec bufferisation des précédents calculs pour éviter les calculs inutiles en cas d'arrivée d'un obstacle mobile sur la trajectoire)
  

Nous avons visualisé les différents algorithmes sur PathFinding

Fonctionnement de l'algorithme A-Star :

• Tout d'abord, on calcule la distance qui sépare le robot du point d'arrivée, et on définit les points interdits par les obstacles. (la zone bleue correspond

à l'obstacle et la zone verte est une zone ou le robot touche l'obstacle. Ces deux zones constituent la zone interdite).

• Ensuite le Robot trouve un premier noeud sur la grille qu'on lui a attribué. Si le noeud n'est pas dans une zone interdite, il sauvegarde ce noeud.

• Il répète l'opération jusqu'à trouver le chemin qui le mènera à l'arrivée
  

• Attention : c'est seulement lorsqu'il aura trouvé le chemin complet que le robot va se déplacer !

Recherche d'une solution pour la localisation

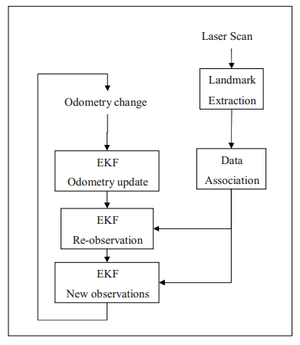
Pour la localisation nous allons utilisé un Algorithme de Localisation et Cartographie Simultanée (SLAM en anglais):

Explicitation des différentes parties :

• Odometry change  : changement de position
• Odometry update  : mise à jour de l'odométrie
• Re-observation  : vérification des changements à partir de toutes les données disponibles
• New observations  : mise à jours de la matrice d'état

• Laser scan  : scan laser brut
• Landmark Extraction : extraction des objets caractéristiques
• Data Association  : association entre objets scannés et objets en mémoire

Ce schéma sera explicité à la séance prochaine.

Semaine 3

Découpage du travail à effectuer

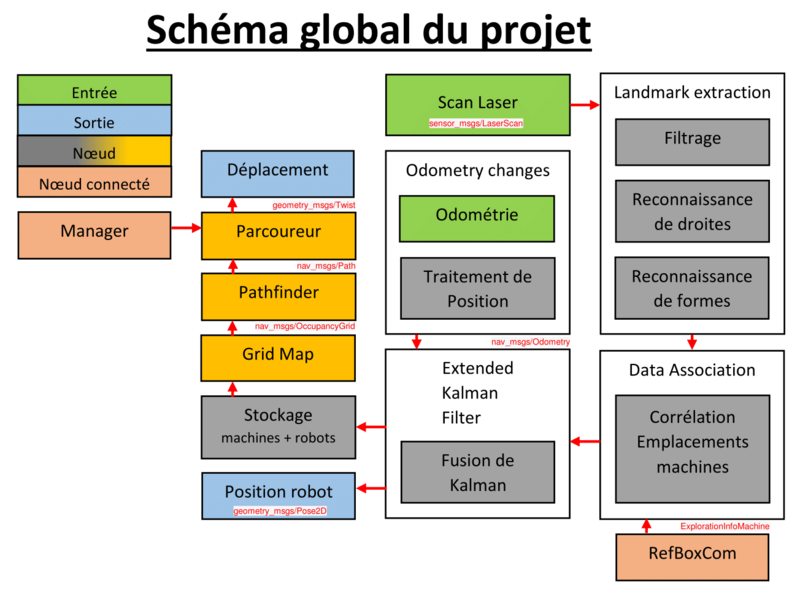
Nous avons découper le travail de génération de map et de la correction de position de la manière suivante :

( Nous recommandons au lecteur de se référer à la partie vocabulaire pour comprendre les termes techniques )

Chaque case du diagramme précédent correspond à un noeud ROS.

Décrivons précisément le rôle de chaque noeud :

• Laser récupère les données brutes du laser.
• Filtrage permet, comme son nom l'indique, d'enlever les éventuels bruits qui affectent les données du laser.
• Reconnaissance des droites traite les données laser filtrées pour détecter les droites présentes (Transformée de Hough ou Ransac)
• Reconnaissance des formes extrapole les objets (machines) à partir des droites.
• Corrélation emplacements machines lie la position des machines détectées au laser et les positions envoyées par RefBoxCom pour éviter les incohérences.
• Odométrie récupère la position du robot par rapport au point de départ. Il renvoie une position corrigée grâce au gyroscope(Pose) et une position non corrigée par le gyroscope (Twist)
• Traitement de position corrige l'erreur sur le Twist avec les données du gyroscope (par dérivation).
• Fusion de Kalman est un algorithme qui va coupler les données de position et les données du laser afin de fournir un modèle et une position précise. C'est le noeud central du SLAM.
• Stockage machines + robot transforme les positions des machines et du robot en grille. Il sera couplé aux détections d'obstacles.
• Grid Map renvoit une map utilisée ensuite pour les déplacements et les calculs de trajectoires (A_Star)
• RefBoxCom stocke et renvoie la position des machines.
• Position robot renvoie la position exacte du robot sur la grille.
• Manager Noeud qui envoie la position à atteindre.
• Pathfinder recherche le chemin demandé par le Manager sur une grille
• Parcoureur exécute le chemin trouvé en fournissant les vitesses au noeud Déplacement.
• Déplacement (noeud robotino_local_move_server), qui donne les commandes aux moteurs à partir de la vitesse linéaire et angulaire envoyée par le Parcoureur.

Recherche de documentation sur ROS et l'API du Robotino

Nous avons cherchés toutes les documentations techniques nécessaires pour la programmation de chaque noeud : Wiki_ROS et API_Robotino, nous permettant de mettre à jour le schéma global, notamment au niveau des types.

Etude de l'algorithme A-star précédent

Nous nous sommes ensuite concentrés sur le noeud GridMap qui contient Map.cpp :

Dans le code de l'an dernier, ce noeud générait une grille en dur. Cependant, cette solution n'est pas possible cette année car nous ne connaissons pas toutes les informations sur la piste (on connaît à peu près la position mais pas l'orientation). Il va donc falloir générer une grille en fonction du noeud précédent qui nous renverra un type OccupancyGrid.

Etant donné que ce noeud tournera en permanence, si des informations changent pendant que le robot est sur la piste (détection des nouvelles machines par exemple), le noeud Map.cpp modifiera la grille en temps réel.

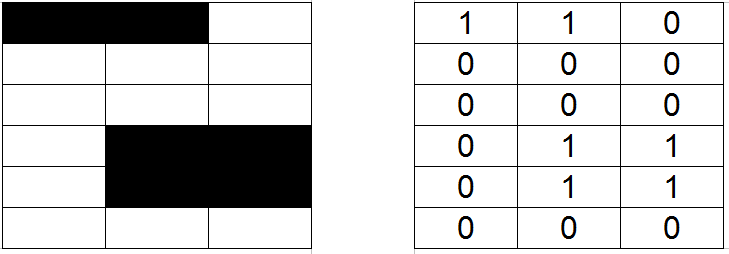
La grille est décomposée en case pour le A-Star :

Si c'est une case interdite (obstacle) ont associe a la case la valeur 1, si elle est autorisée, on associe la valeur 0. On illustre le principe précédent par un exemple :

Cependant, le noeud "Grid Map" va nous délivrer un vecteur et non une matrice par le biais de OccupancyGrid.Data.Dans notre exemple précédent, on récupère le vecteur suivant :

On choisit donc de transformer ce vecteur en matrice, car l'algorithme A-Star fonctionne sur un graphe, pas un vecteur. On connait la largeur (en case) de la grille grâce au type OccupancyGrid.info.width.

Le pseudo-code pour générer la matrice à partir de ce vecteur sera le suivant :

fonction create_grid (OccupancyGrid.Data vecteur[size]) : matrice[height].[width]
{
  matrice[height].[width] ;		
     int t <- size;
         Pour (i de 0 à height)
         faire:
               {
                   Pour (j de 0 à width)
                   faire :
                           {
                              matrice[i].[j] <- vecteur[t] ;
                              t++;
                           }
               }
  return matrice;
}

Semaine 4

Localisation - Landmarks Extraction

Nous nous concentrons essentiellement sur la première partie, qui est la partie : "Landmarks Extraction" (extraction des points de repères). On travaille ici dans le repère du laser, qui est différent de celui du robot, et du global. La transposition dans le repère global se fera dans la partie "Data Association". On doit ainsi, dans l'ordre :

☑ récupérer des données lasers via le topic /scan
☑ convertir les coordonnées polaires en coordonnées cartésiennes en filtrant les données aberrantes (> range_max et < range_min)
☑ implémenter l'algorithme RANSAC (Random SAmple Consensus) de détection de droites :
☑ détecter la "meilleure" droite à partir des points en sélectionnant aléatoirement des combinaisons de points
☑ stocker le meilleur modèle (angle + tableau de points)
☑ recommencer tant qu'il reste assez de points à traiter (5)
☐ extraire les segments à partir des modèles trouvés et des points
☐ extraire les points extrèmes
☐ calculer la taille du segment
☐ grouper les segments qui appartiennent potentiellement à une même machine
☐ chercher des angles droits, des segments de 35 ou 70 cm (largeur et longueur d'une machine)
☐ extrapoler les positions des machines dans le repère du laser
☐ définir le barycentre de la machine ainsi que son angle
☐ stocker ces positions

Pathfinder

Nous avons aussi pris du temps avec Valentin VERGEZ, qui a développé, l'an dernier, les codes pour le déplacement du Robotino et le calcul de trajectoire

Nous avons éclairci quelques points sur cette partie du projet :

• Les commentaires sur l'utilité de chaque fonction ont été rajoutés.
• Le "code mort" a été nettoyé ainsi que les parties inutiles.
• Nous devons trouver un moyen de tester cette partie du code seule. (A priori graphiquement).

Etant donné l'arrivée d'un nouvel ordinateur au sein de l'équipe, nous en avons profités pour installer les logiciels qui nous permettrons de faire tourner les noeuds codés sur les Robotino :

• Installation d'Ubuntu 12.04 ( c'est cette version qui permet de faire tourner ROS Hydro)

• Installation de ROS Hydro (ensemble d'outils informatiques open source permettant de développer des logiciels pour la robotique.)

• Installation des paquets nécessaires (catkin, Desktop Install, ROS-Base, Individual Package)

• Installation de GIT (outil de bas niveau permettant de gérer l'évolution du contenu d'une arborescence)

• Vérification que toutes les fonctionnalités de ROS Hydro étaient présentes ( Tutoriel)

La récupération du code complet de l'année dernière et une solution a été trouvée afin de tester le code de génération de trajectoire A-star:

• Pour visualiser une Map ainsi qu'un Path (chemin), on peut utiliser l'outils RVIZ.
• Dans RVIZ, on peut ajouter un Path (topic /path), ainsi qu'ajouter une Map (/grid): Ceci correspond exactement à ce que nous souhaitons visualiser pour la partie calcul de trajectoire.
• Pour publier une Map fictive, on executera le script fakeGrid.sh
• Pour générer un chemin, on lancera le pathfinder (rosruns rbqt_pathfinder server : notre code) et on effectuera une requête avec le script pathReq.sh.

Si tout se passe correctement, le chemin devrait s'afficher en vert sur la map.

Nous avons aussi du communiquer notre avancement aux autres parties de l'équipe. Le schéma général ainsi qu'un outil permettant d'expliquer les différents algorithmes de recherche de trajectoire optimale nous ont aidé à leur communiquer nos objectifs et les processus choisis.

L'algorithme A-Star que nous allons utiliser donne le résultat final suivant (utilisation du site PathFinding ):

• le chemin optimal calculé par A-Star
• le point de départ
• le point d'arrivée
• les points interdits (obstacle)
• les points que l'algorithme a déjà calculé
• les points que l'algorithme aurait calculé à la prochaine itération

Localisation - Landmarks extraction - filtrage

Dans cette partie, nous avons commencé à définir une classe laserScan qui contient la fonction polarToCart, elle convertit les données laser (tableau de ranges) en liste de points (x,y) :

void laserScan::PolarToCart (){
 Point p;
 for (int i=0; i<m_ranges.size(); i++){
   if((m_ranges[i]>getRangeMin()) && (m_ranges[i]<getRangeMax())){
     p.setX(m_ranges[i]*cos(getAngleMin() + i*getAngleInc()));
     p.setY(m_ranges[i]*sin(getAngleMin() + i*getAngleInc()));
     m_points.push_back(p);
    }
  }
}

Localisation - Landmarks extraction - reconnaissance de droite

Dans cette partie, nous avons déterminé quel algorithme nous allons utiliser : RANSAC. L'algorithme de RANSAC trouve la meilleure droite dans un nuage de points. On itère plusieurs fois cet algorithme afin de trouver l'ensemble de toutes les droites du scan laser. On a donc en sortie une liste des droites composants le nuage de points initial.

Entrée : listOfPoints    -> liste de points initiale 
Sortie : meilleur_modèle -> les paramètres de la droite qui correspondent le mieux aux points
                         -> tableau de points à partir desquels la droite a été estimée
                         -> erreur du modèle de droite par rapport aux points

tant que la liste contient assez de points
 itérateur := 0
 meilleur_modèle := aucun
 tant que itérateur < k (fixé par une loi de probabilité)
  on choisit deux points au hasard dans la liste
  on fabrique un modèle_possible à partir de ces deux points
  Pour chaque point de la liste qui ne sont pas dans le modele_possible
   si le point s'ajuste au modele_possible avec une erreur inférieure à t
    Ajouter ce point au modele
   si le nombre de points dans le modele est suffisant pour valider l'existence du modele
    erreur := coefficient de corrélation de la régression linéaire de ensemble_points
   si erreur < erreur du meilleur_modele
    meilleur_modèle := modèle_possible

 stocker meilleur_modèle dans liste de modèles
 retirer meilleur_ensemble_points de la liste des points initiale
 recommencer avec la liste modifiée

Semaine 5

Localisation - Landmarks Extraction - reconnaissance de droite

Nous avons adapté l'algorithme précédent afin de mieux correspondre aux structures que nous avons créées :

• Modele
  • Liste de points
  • Liste d'indices
  • Corrélation
  • Droite
    • Point
    • Angle
  • Segment
    • Point "min"
    • Point "max"
    • Angle
    • Taille

Nous avons aussi codé toutes les fonctions nécessaires dans l'algorithme de Ransac, dont celle permettant la correction de l'approximation de droite par régression linéaire des points correspondants à un modèle trouvé (linReg()) qui nous a donné matière à réflexion. Aussi, notre première idée qui était de travailler avec des std::vector a du changer puisque l'aspect récursif de l'algorithme que nous allons utiliser nécessite de multiples suppressions sur les données à entrer dans l'algorithme de Ransac. On travaille donc maintenant avec des std::list.

Tous nos codes sont disponibles sur la branche feature/navigation/SLAM du GIT de l'équipe PyroTeam.

Semaine de vacances de février

Localisation - Landmarks Extraction - reconnaissance de droite

Nous devons réaliser un noeud permettant de valider notre algorithme, c'est-à-dire implémenter sous ROS notre code C++ afin de tester, soit directement sur le robot, soit avec des bagfiles. Cette étape est très importante pour pouvoir passer à la suite : extrapoler les droites trouvées en segments puis en objets.

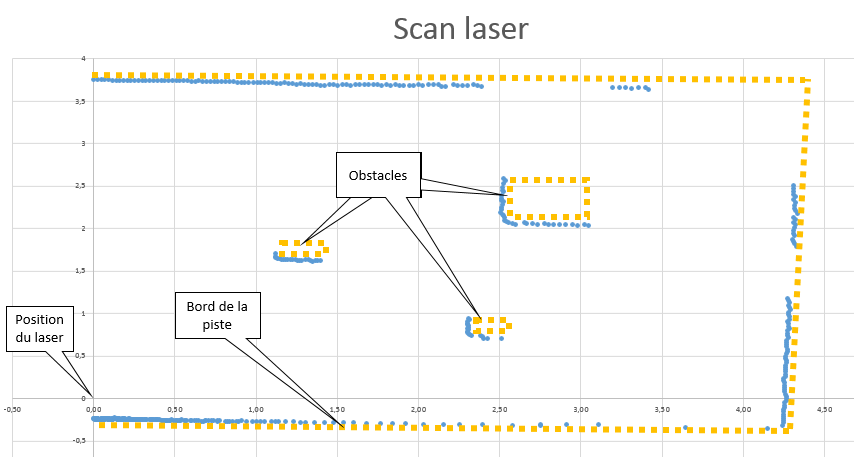
Notre programme consistant à reconnaître les droites à partir du scan laser est fonctionnel et a été testé à partir du scan laser suivant :

Processus de validation :

• Lancer le programme rosrun localisation test_polar_to_cart

résultat : on trouve 5 droites

m = -0.0229637 p = -0.24079
nb de points dans la droite : 246
coeff de correlation : 0.812376

m = -0.0315132 p = 3.7506
nb de points dans la droite : 102
coeff de correlation : 0.928089

m = 32.9243 p = -139.943
nb de points dans la droite : 77
coeff de correlation : 0.914475

m = 7.04634 p = -15.42
nb de points dans la droite : 32
coeff de correlation : 0.970724

m = 0.253029 p = 1.32235
nb de points dans la droite : 28
coeff de correlation : 0.979578

ce qui correspond à l'image suivante :

On voit que la recherche de droite marche bien, mais peut être améliorée en ajoutant des conditions de proximité des points correspondants à une seule droite, pour éviter le phénomène que l'on voit au milieu. Le résultat après avoir ajouté cette condition et en ayant affiné au maximum les paramètres, au dépend d'un temps de calcul beaucoup plus élevé (10 secondes au lieu de moins d'1 seconde)  :

Pour valider l'algorithme de régression linéaire nous avons :

• Récupéré tous les points correspondants à chaque droite
• Rentré ces points sur Excel
• Fait une courbe de tendance
• Affiché l'équation de droite et le coefficient de corrélation
• Comparé avec ce qu'a trouvé notre programme
• Conclu que notre programme était bon

suite des événements : Faire plusieurs tests avec d'autres scans laser pour ajuster les paramètres.

== Fichiers Rendus ==