Cheval Bionique
Réalisation d'une patte de cheval bionique
Avant propos
Dans le cadre d'une convention signée en 2013 entre Polytech Lille, FESTO [1] Didactic et les Compagnons du Devoir [2] en 2013, il a été décidé la création d'un cheval bionique pour l'horizon 2015. C'est donc dans le cadre de cette convention que notre sujet de Projet de Fin d'Études (PFE) se pose.
Cette patte, fabriquée en collaboration entre les départements Informatique-Microélectronique-Automatique (IMA) et Conception Mécanique (CM), a pour but premier d'étendre le champ de vision des technologies mécatroniques, et de les démocratiser dans le monde étudiant par la suite.
La bionique, et le biomimétisme par association, a pour but de s'inspirer directement de la Nature et de ses "produits", afin d'en faire une reconstitution technologique fidèle, et élargir ainsi nos domaines d'application. Les technologies actuelles et futures allant en ce sens, la conception d'une patte bionique de cheval est un défi de taille pour ce PFE, et tout aussi valorisant pour notre diplôme.
Description du modèle
La réalisation de cette patte de cheval bionique se fera à l'aide de matériel provenant de FESTO pour une grande partie. En effet, pour la réalisation des muscles, nous utilisons les muscles pneumatiques développés par FESTO. Leur principe est simple : en injectant de l'air comprimé dans celui-ci, le muscle va se contracter comme le ferait un muscle organique, et sera relâché quand il n'y aura plus d'air.
Pour rester au plus près de la Nature, nous utiliserons six muscles pneumatiques, pour trois segments mobiles. Ces segments seront des laminés censés représenter les os d'une patte. À chaque segment seront attribués deux muscles, pour respecter l'antagonisme de ces derniers.
Enfin, des liaisons rotules assureront le lien entre les segments. Une fois tous ces éléments assemblés, la contraction et le relâchement des muscles animera la patte d'un mouvement proche de celle d'un cheval.
Objectif
Après avoir fournit un premier livrable pour la date du 24 Octobre 2013, devant des membres de FESTO, des Compagnons du Devoir, de la Région et de l'École qui ont assisté à une première démonstration, le but est avant tout d'obtenir un mouvement réaliste de la patte bionique.
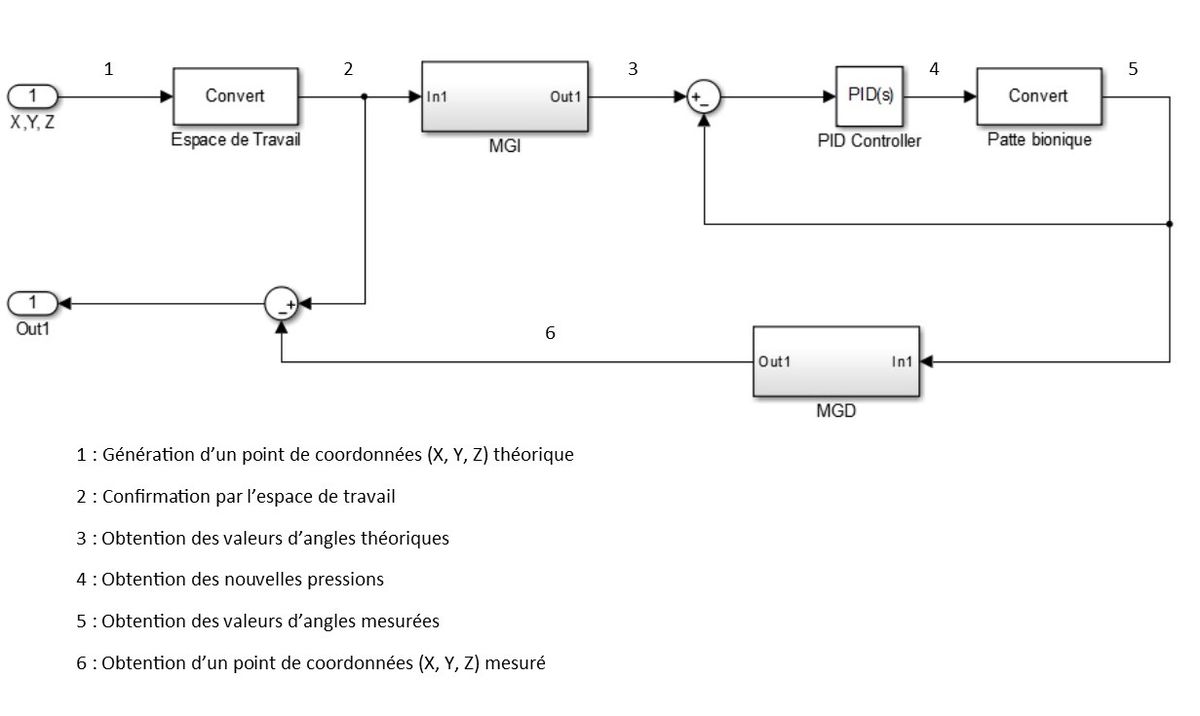
La jambe bionique doit être conçue pour pouvoir être régulée au moins en pression, après en position, et fonctionnant en boucle fermée. Ainsi l'utilisateur doit être en mesure d'exiger de la patte qu'elle se rende en une position déterminée, et que celle-ci se régule afin d'y rester.
Journal de bord
Prise en main du sujet
Il s'agit en effet d'un projet très ambitieux, qui engage Polytech Lille, et donc les étudiants qui travaillent dessus. Un stage d'IMA4 a été réalisé sur ce sujet ; il nous faut donc nous adapter au travail réalisé. Dans un premier temps, nous avons l'occasion de faire le bilan matériel nécessaire à la bonne réalisation de la patte bionique. L'étude porte sur ces différentes parties :
- Modélisation d'ensemble de la patte de cheval - Recalcul et redimensionnement des segments et rotules - Concertation avec les étudiants CM sur la réalisation et le montage effectif de la patte.
Voici les données du modèle définitif adoptées : 4 segments, dont 3 amovibles et 1 relié au bâti ; 3 paires de muscles pour l'antagonisme sur chaque segment en mouvement ; 3 rotules.
Bien que leur utilisation interviendra plus tard, nous passons à la réalisation des encodeurs, sur base de HEDS-5X40. Leur rôle sera de renvoyer la valeur de l'angle via DSpace qu'il y a entre deux segments. Ces encodeurs, au nombre de trois, seront placés au niveau des rotules de la patte.
À la réception de l'ensemble des éléments, ce qui a pris pas mal de jours, nous pouvons enfin passer au montage final de la patte avec les encodeurs. Tout d'abord, nous réalisons l'assemblage des muscles avec les vannes d'air et bouchons d'échappement. Puis on passe au montage de chaque laminé avec une rotule servant d'articulation, et quatre demie-rotules assurant le rôle des ligaments.
Comment fonctionne la patte ?
Le but premier est de faire se mouvoir la patte grâce aux muscles pneumatiques FESTO. Ces derniers ont une tolérance maximale de 6 bars. C'est-à-dire qu'en injectant une pression de 6 bars dans un muscle, ce dernier sera rétracté au maximum. En pratique, leur taille passe alors de 40 cm au repos à 35 cm comprimé.
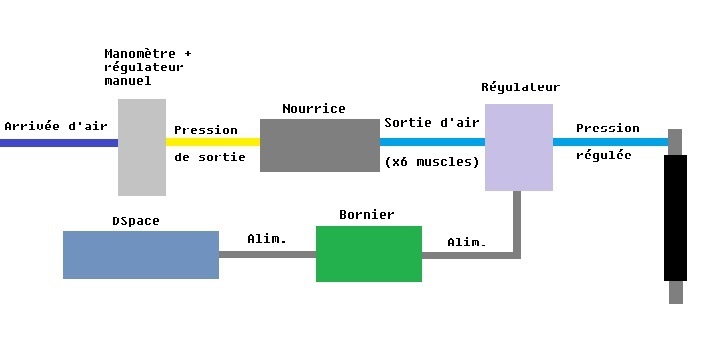
Nous disposons dans notre salle de projet d'une arrivée d'air. Mais sa valeur est constante, il faut donc pouvoir faire varier cette valeur afin qu'elle soit adaptée à notre environnement. Nous relions alors l'arrivée d'air à un manomètre pour obtenir 6 bars, puis on passe dans une nourrice afin d'obtenir 6 entrées de pression de même valeur.
En parallèle de cette solution hardware, on développe sur ControlDesk une plateforme de contrôle de pression à base de potentiomètres et qui sera implémentée dans la DSpace, ainsi qu’un programme de commande Matlab Simulink. En reliant la DSpace à l’ordinateur et un bornier, nous sommes en mesure de faire varier une tension de commande.
Ainsi, nos sorties d’air et ces tensions de commandes sont reliées à un régulateur qui, en fonction de la tension qu’il reçoit, fournira une pression proportionnelle à celle-ci. On répète donc ce système pour chaque muscle indépendamment, et nous sommes en mesure de contrôler la compression de chaque muscle de la patte par ordinateur. Les 6 régulateurs sont alimentés sous 24 V.
Rectification de l'architecture
Nous pouvons procéder en l'état actuel des choses aux phases de test sur un premier segment. Nous cherchons à définir l'amplitude maximale - le débattement - que possède un segment par rapport à un autre. Cette phase d'évaluation du débattement nous sera utile pour la définition de l'espace de travail de la patte.
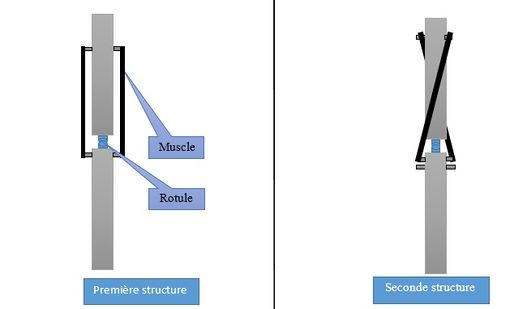
Dans un premier temps, pour imiter au mieux la Nature, nous sommes partis sur une structure de muscles antagonistes, c'est-à-dire un muscle d'un côté et de l'autre parallèles au segment, comme on peut le retrouver dans le bras humain (biceps/triceps).
Les phases de tests avec cette architecture nous fournissent un débattement de 30° environ, ce qui est assez faible. Nous choisissons donc de modifier cette architecture pour obtenir un meilleur débattement, même si la patte perd de son côté "naturel". On part donc sur une structure de muscles antagonistes croisés, ce qui nous permet d'obtenir un débattement de 50° par segment.
Commande de la patte
L'espace de travail
Définir un espace de travail consiste en l'établissement des frontières physiques de notre système. En d'autres termes, nous devons définir mathématiquement et informatiquement l'ensemble de la zone couverte par le point final de notre patte. Ce point final sera la fin du segment le plus bas (juste avant la cheville NAO).
Nous nous servons de Matlab pour définir cet espace. Pour considérer et modéliser l'ensemble de notre espace de travail, et donc tracer tous les points atteignables par la patte, il faut prendre en considération chaque point que peut atteindre chaque segment, et faire varier l'angle de débattement.
Il faut donc imbriquer trois boucles (une pour chaque segment mobile) les unes dans les autres pour obtenir l'affichage de notre espace de travail. Le problème qui se pose est la longueur de l’exécution du programme (plusieurs jours pour les machines les moins performantes), si bien que nous n'avons jamais pu obtenir l'ensemble de notre espace de travail de manière correcte.
La solution était alors de n'afficher "que" les frontières de notre espace de travail, en considérant que tout point se trouvant à l'intérieur de ces frontières était un point de notre espace de travail.
Le Modèle Géométrique Indirect (MGI)
Une fois les coordonnées du point final acquises, on souhaite déterminer les paramètres articulaire à affecter au niveau de chaque rotule pour pouvoir atteindre le point les cordonnées souhaités.
Problème : Nous ne pouvons réaliser la MGI qu'en passant par des approximations. En effet, nous avons des solutions infinies pour rejoindre un point précis. Appliquer un algorithme de résolution à partir du MGD comme ceux que nous avons vus l'an dernier en cours de robotique s'avère possible mais nous avons alors des solutions complexes, ce qui est inutilisable pour nous.
Solution : Pour résoudre la complexité de la solution, nous avons décidé de fixer le premier angle et d'évaluer les deux autres angles en fonction de celui-ci, tout en prenant en compte le fait que nous avions un débattement limité.
Problème logiciel : Nous avions utilisé la fonction Matlab rand() afin de générer un nombre aléatoire pour fixer le premier angle. Mais la compilation de pouvait être effectuée avec la DSpace en raison de l'âge de notre version de Matlab (2006). Du coup, une valeur fixe a été attribuée à l'angle pour pouvoir être sûr de compiler.
Le Modèle Géométrique Direct (MGD)
Le MGD s'établit en fonction des longueurs de segments et des relations angulaires qui interviennent entre les segments. On utilise deux méthodes pour vérififer ce modèle : la méthode du calcul direct, et la méthode de Denavit-Hartenberg. L'objectif est de rentrer des valeurs d'angles dans Matlab et que l'on obtienne en retour la position dans l'espace de notre point final (ici, le bout du dernier segment de la patte).
Ci-dessous, on peut lire le code matlab de l'exécution du modèle géométrique direct. À valeur d'exemple, on intègre au modèle trois valeurs d'angles q1, q2 et q3 (respectivement 25°, 0° et 0°) immédiatement convertis en radians.
La matrice D intègre ces angles dans son calcul et on obtient en sortie deux résultats qui correspondent aux coordonnées (X, Y) du point final selon les angles choisis
clear all close all clc %Définition des variables d'angle q1=25*pi/180; q2=0*pi/180; q3=0*pi/180; %Matrice MGD D=[0.40+0.43*(cos(q1)+cos(q1+q2))+0.51*((cos(q3)*cos(q1+q2))-(sin(q3)*sin(q1+q2))) ; 0.43*(sin(q1)+sin(q1+q2))+0.51*((cos(q3)*sin(q1+q2))+sin(q3)*cos(q1+q2)) ; ]
Pour pouvoir réaliser une MGD, il faut au préalable modéliser entièrement le système et créer un référentiel spatial pour chaque segment de la patte, car leur mouvement indépendant fait que deux segments ne partagent pas le même référentiel géométrique. Reste à définir les relations entre les angles pour pouvoir exprimer les coordonnées d'un point d'un référentiel, dans un autre référentiel.
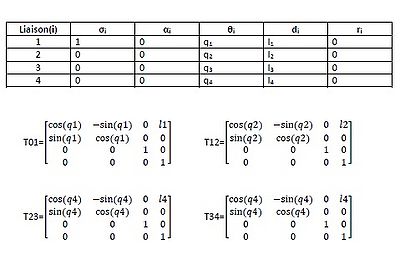
L'objectif de la méthode de Denavit-Hartenberg est de valider les résultats obtenus, car c'est cette méthode qui sera implémentée dans notre modèle. Pour ce, il nous faut 5 paramètres : 1 pour un angle de translation, 2 pour les angles de rotation, et 2 distances entre les axes.
On calcule les matrices de passage grâce à ces paramètres (une matrice correspond à une transition entre deux segments), puis ces matrices sont multipliées entre elles et on récupère le même système d'équation que par la méthode du calcul direct.