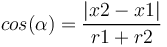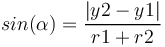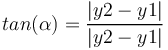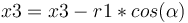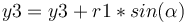IMA5 2022/2023 P20 : Différence entre versions
(→Semaine 6 (21/11/2022 - 26/11/2022)) |
(→Semaine 7 (5/12/2022 - 16/12/2022)) |
||
| Ligne 283 : | Ligne 283 : | ||
*Finalisation de la démo "faire bouger une balle avec un objet" | *Finalisation de la démo "faire bouger une balle avec un objet" | ||
| − | =Semaine 7 (5/12/2022 - 16/12/2022)= | + | |
| + | = <div class="mcwiki-header" style="border-radius: 10px; padding: 20px; font-weight: bold; text-align: center; font-size: 80%; background: #9FE7FF; vertical-align: top ; width: 100%;">Semaine 7 (5/12/2022 - 16/12/2022)</div> = | ||
*Configuration de l'ordinateur en E306 | *Configuration de l'ordinateur en E306 | ||
Version du 27 décembre 2022 à 20:49
Sommaire
- 1 Présentation générale
- 2 Semaine 1 (05/09/2022 - 09/09/2022)
- 3 Semaine 2 (19/09/2022 - 23/09/2022)
- 4 Semaine 3 (3/10/2022 - 9/10/2022)
- 5 Semaine 4 (17/10/22 - 21/10/22)
- 6 Semaine 5 (7/11/22 - 10/11/12)
- 7 Semaine 6 (21/11/2022 - 26/11/2022)
- 8 Semaine 7 (5/12/2022 - 16/12/2022)
- 9 Amélioration de la simulation
- 10 Liens externes
Présentation générale
Contexte
En 2015 des étudiants de la filière IMA de Polytech ont réalisé une table connectée comportant un écran tactile pour leur projet de fin d'études. Cette table est aujourd'hui inexploitée.
Objectifs
L'objectif de ce projet est donc de créer un jeu de billard en réalité augmentée en profitant des caractéristiques de la table. En plus d'offrir une expérience unique grâce à une caméra qui permet de jouer avec une queue adaptée similaire à celle d'un véritable billard. Il sera également possible de suivre les parties grâce à une application mobile sur un appareil connecté en Bluetooth à la table.
Historique
Ce projet sera le deuxième projet réalisé sur cette table connectée, après la réalisation en 2018 d'une table de bar connectée par des étudiants en IMA de Polytech Lille. [1]
La réalisation de la table de billard a été fait par sur ce wiki [2]
Cahier des charges
Fichier:P20 2022 2023 cahier des charges.pdf
Cahier des spécifications
Fichier:P20 2022 2023 cahier des spec.pdf
Diagramme de Gantt prévisionnel
Semaine 1 (05/09/2022 - 09/09/2022)
- Réalisation du cahier des charges
- Ébauche d'un diagramme de Gantt prévisionnel en début de projet
- Étude des moyens disponible pour la réalisation de l'interface graphique
- Étude des mathématiques appliquée au billard
- Étude de la collision entre deux boules
- Commencer la constructions des classes pour l'interface
Choix du langage
a simulation sera intégralement codé en langage Java pour ces raisons :
- Ce langage est l'un des plus rapide sur l'exécution par rapport au langages orientée objet concurrent (par exemple C++ ou Python)
- Ce langage est un langage que nous connaissons bien, notre choix est pour respecter les échéances
Étude des mathématiques appliquée au billard
Calcul de collision entre deux balles
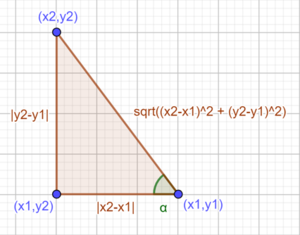
Il faut calculer si deux balles sont en collision, il existe une façon simple de calculer cette collision. Soit deux objets circulaire :
- C1 de centre (x1,y1) et de rayon r1
- C2 de centre (x2,y2) et de rayon r2
Si on imagine une ligne entre les deux centres des cercles, la distance D qui sépare les deux centres est :
-
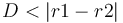 si les deux boules sont en collision
si les deux boules sont en collision -
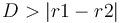 si les deux boules ne sont pas en collision
si les deux boules ne sont pas en collision
Pour faire l'algorithme de collision, il suffit de vérifier que :
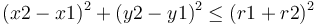
Il est aussi possible de calculer l'angle α à partir de formules basique de trigonométrie :
Et éventuellement le point de collision (x3,y3) à partir du centre de la boule C1 (x1,y1,r1) :
Semaine 2 (19/09/2022 - 23/09/2022)
- Réalisation du cahier des spécifications
- Étude sur le choix du matériau pour la queue
- Brainstorming sur la hiérarchie de nos classes java
- Étude mathématique :
- Étude de la friction de la table
- Étude de la collision avec un mur
- Étude de la réponse de collision avec une boule
- Codage de la classe "Renderer" pour la simulation graphique
Hiérarchie de nos classes java
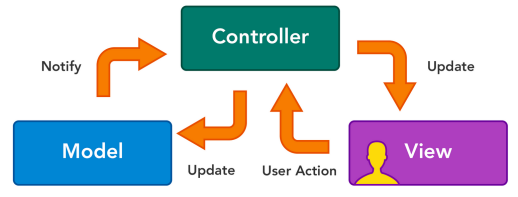
Notre simulation fonctionne selon le modèle MVC en java :
Ce modèle nous permettra de nous retrouver plus facilement dans nos classes. Pour faire simple :
* la vue qui s’occupe uniquement de l’affichage d’un modèle. * le modèle représente un objet, une classe, les données de l’application. * le contrôleur est le composant qui s’occupe de mettre ces deux entités en relation, il est comme le cerveau de l’application,
Nous avons prévu alors de mettre dans les vues :
- Des classes Vues qui dessinera chaque modèle
- Une classe Renderer qui s'occupera de récupérer les classes Vues et les affichera sur l'écran
En modèles :
- Une classe Ball dans lequel sera codé les méthodes de calcul de la physique des balles ainsi que leurs attributs (taille, type, numéro, position, vitesse) elle sera imprimable en vue
- Une classe Hole dans lequel sera codé les méthodes de calcul de collision entre un trou et une balle ainsi que leurs attributs (tailles, position), elle sera également imprimable par un le biais d'une vue
- Une classe Player qui possèdera certains attributs : type de balle qu'il possède, ID, ... Elle ne sera pas imprimable
- Une classe TableJeu qui possèdera la méthode de mise à jour itératif de la table de jeu, elle aura comme attribut les balles, les trous ainsi que les règles.
- Une classe Rules qui gèrera les règle de jeu du billard (8 américain)
Et les contrôleurs seront :
- Les classes Listeners qui auront pour but de lire les actions de l'utilisateur (action à la souris ou au clavier)
- La classe Main qui initialisera les classes de vues, les listeners ainsi que la table de jeu, et qui gèrera itérativement le jeu entier
Nous allons aussi créer un répertoire libs dans lequel nous coderons des classes basique telle que une classe de point ou des constantes pour notre simulation
Étude des mathématiques appliquée au billard
Généralités sur le mouvement en deux dimensions
La boule sera soumise à une vitesse à deux dimensions (selon l'axe des x et y), où la vecteur vitesse se calcule de la sorte : 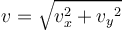
La nouvelle position de la boule à un intervalle de temps donnée sera 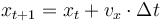 (de même pour l'axe des y)
(de même pour l'axe des y)
La nouvelle vitesse de la boule à un intervalle de temps donnée doit être calculé selon son vecteur vitesse et l'accélération, alors :
- on calcule son vecteur vitesse
- on normalise les deux vitesse de l'axe des x et y en divisant ces derniers par le vecteur vitesse (cela permet de garder en mémoire le sens ainsi de l'angle du vecteur vitesse).
- On applique l'accélération au vecteur vitesse où :
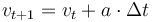
- Finalement, on recalcule les vitesses en deux dimension en multipliant (3) par (2)
Estimation de l'accélération de la boule
La boule est soumise à une seule force pendant sa course : sa déaccélération
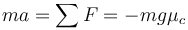
Réponse de collision avec le mur
Ici c'est simple,
- le mur du haut et du bas aura pour effet de changer le sens de la vitesse de la balle sur l'axe des x, en d'autres termes, si la vitesse était positive, alors elle sera négative et vice-versa.
- le mur de gauche et de droite aura le même effet mais pour l'axe des y
Réponse à la collision entre deux balles
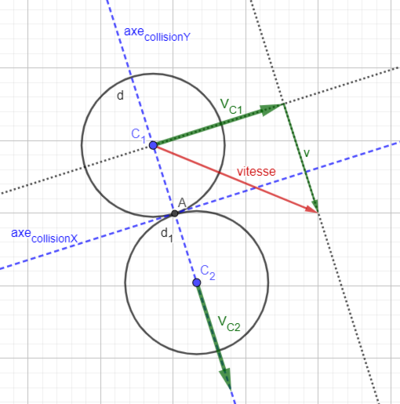
Dans un premier temps, on dissout les vitesses des deux boules selon l'axe de collision. Puis on calcule la valeur scalaire de ces nouvelles vitesses.
Ainsi, les vitesses initiales seront décomposés en deux composantes:
- Une composante transmis à l'autre boule égale à la vitesse transmis selon l'axe de collision (décomposée sur l'axe des x et y)
- L'autre composante, est la vitesse gardée par la boules, qui sera le résultat de la soustraction entre la valeur scalaire de la vitesse initial et la vitesse transmise à l'autre boule
Semaine 3 (3/10/2022 - 9/10/2022)
- Avancée sur l'interface graphique
- Réalisation de la table
- Réalisation du design des boules
- Codage des algorithmes de mise à jour de la table de jeu
- Tests des algorithmes
- Réponse de collisions sur les murs marche
- Réponse de collisions sur les boules marche
- Mise à jour des vitesses et positions marche
Bugs connu à ce jour sur notre simulation :
- Certaines boules reste en collision, ce bus arrive rarement, mais une correction devra être nécessaire pour corriger ce bug.
- Bug de pleine écran sur les machine Debian
Réalisation de l'interface graphique
Nous réalisons l'interface graphique en utilisant la librairie Swing de java qui nous permet de créer facilement des interfaces graphiques, trois sont éléments sont essentiels dans notre interface :
- la table de jeu
- les boules
- les trous
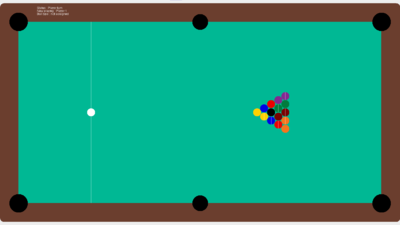
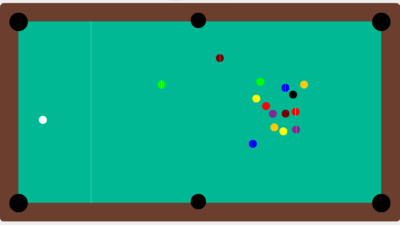
Ceci étant fait, on obtient ce résultat : (en positionnant les boules au bons endroit pour simuler le coup de casse)
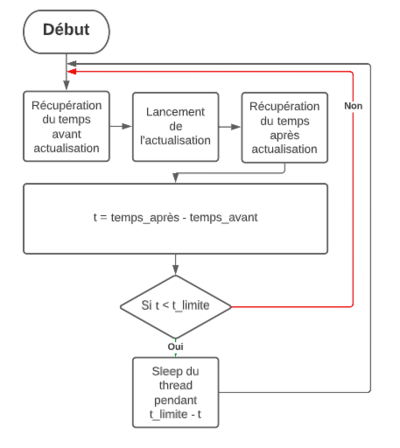
Nous devons mettre à jour l'interface dans un temps fixe, pour cela nous créons dans la classe Main un thread quand lequel nous rafraichissons l'interface graphique tout les 20ms (soit 50 images par secondes)
Algorithme de mise à jour de la table
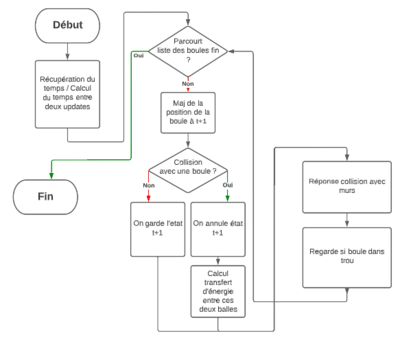
On a codé la méthode BallTable.update(), qui à pour effet de mettre à jour les positions des balles ainsi que leurs vitesses. Cette méthode applique cet algorithme :
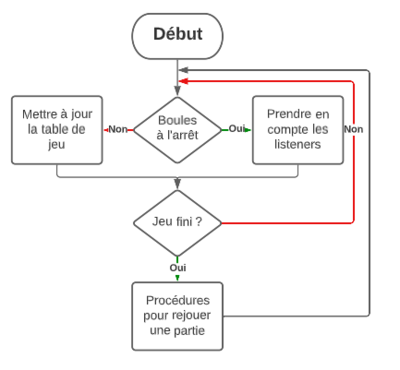
Algorithme de la boucle main
Tests des algorithmes du modèle physique
On teste d'un seul jet les collisions et réponses avec un mur et avec une boule :
Semaine 4 (17/10/22 - 21/10/22)
- Avancée sur l'interface graphique / simulation
- Intégration des listeners
- Tests des algorithmes sur la coup de casse
- Débug des bugs connus (bug de collision et bug de plein écran)
- Amélioration de l'interface graphique
- Apprentissage de la technologie OpenCV pour le traitement d'image
Intégration des listeners
Les listeners vont nous permettre des tirer sur la boule blanche et la replacer temporairement (ce sera remplacé par le traitement d'image plus tard), voici le résultat :
Tests de la simulation
1er jet
Le premier jet, utilisait l'ancienne méthode d'affichage, le freinage de la table n'était pas non plus pris en compte, les boules ne décéléraient donc jamais. Les listeners n'étaient pas encore implémentés. Et les trous n'étaient pas non plus fonctionnels.
L'exécution se fait sur un ordinateur avec Windows, les collisions marchent correctement, on remarque seulement quelques fois un problème de boules qui se rentrent dedans : Ce problème peut-être du à :
- Un problème sur le calcul de collision
- Un problème sur le temps d'exécution, un temps trop élevée et la boule peut rentrer dans une autre à la prochaine mise à jour des positions
Dès l'exécution sur un PC Debian de l'école, la simulation s'ouvre 1 fois sur 3, le cas échéant, la simulation est très différente de l'exécution sur Windows. La barre des tâches en haut de l'écran n'est pas recouverte par l'application en plein écran, de plus, les éléments graphiques sont tous décalés comme si l'application ne pouvait afficher que sur la partie en dehors de la barre des tâches mais qu'elle prenait la largeur et la hauteur totale de l'écran pour les coordonnées.
Ce bug a vite été résolu en utilisant une différente API pour mettre l'application en plein écran.
2ème jet
Dans ce deuxième jet, le problème de plein écran sur les machine Debian est corrigé. Les trous sont fonctionnels. On implémente les listeners pour pouvoir tirer dans la boule blanche, le but est de savoir si la simulation répond bien lors du coup de casse (le premier coup dans une partie de billard est celui où il y a le plus de collision). Sur ce jet, le problème des collisions de boules n'est pas encore entièrement corrigé, pour voir si le problème persiste dans ce cas.
On remarque que le bug de collision est très présent. De plus, il est impossible de jouer le prochain coup quand ce bug est présent. En effet, même si les boules ne bougent pas, la simulation considère que leur vitesse n'est pas nulle et elle empêche donc que le prochain coup soit joué. La prochaine étape est de corriger ces problèmes.
3ème jet
On remarque que certaines collisions se calculent deux fois dans la même boucle de calcul. L'idéal serait de n'avoir qu'un seul calcul de collision, on donne alors un tableau de 16 booléens à chaque boule pour savoir si la collision entre les boules a déjà été calculé. A chaque fin de boucle, on remet à zéro le tableau de booléen de la boule correspondante.
On remarque une amélioration que ce bug ne s'est pas produit, cependant il existe toujours, il va donc falloir le supprimer définitivement. Avec la nouvelle méthode de calcul, les boules se détachent plus facilement lorsque le bug se produit. Ce patch corrige également l'impossibilité de jouer le coup quand le bug de collision est présent.
4ème jet
On crée un flag pour savoir si la collision entre deux boules est fait, si c'est le cas, alors on ne calculera pas la collision tant que les deux boules seront superposées. Ce patch supprime la fait que deux boules de recalcule leur nouvelles vitesse à chaque itération mais ne le supprime pas totalement
5ème jet
Nous avons remarqué que lors de la casse, les boules étaient déjà en collision (à cause des flottants), on règle ce problème et on ajoute une distance supplémentaire entre chaque boule, nous n'avons plus le bug mais les collisions entre les boules sont très mauvaises(voir ci-dessous)
Semaine 5 (7/11/22 - 10/11/12)
- Élaboration du rapport de mi-projet
- Préparation des slides pour la soutenance
- Début de restructuration de notre projet
- Brainstorming pour la suite des opération
Semaine 6 (21/11/2022 - 26/11/2022)
- Finalisation beta de la simulation de billard
- Recherche et tests de patch pour le bug de collision
- Début du projet avec OpenCV
- Finalisation de la démo "faire bouger une balle avec un objet"
Semaine 7 (5/12/2022 - 16/12/2022)
- Configuration de l'ordinateur en E306
- Mise en place de la table de jeu
- Intégration du code sur la table connecté
- Intégration de la simulation
- Intégration de la démonstration OpenCV
- Détection d'objets sur la table
- Détection de la position de l'écran
- Détection de la queue et mise à jour du curseur sur la simulation
- Amélioration de la simulation
- Restructuration du code
- Amélioration de l'algorithme des règles
- Affichage du statut des joueurs
- Amélioration du modèle physique
Amélioration de la simulation
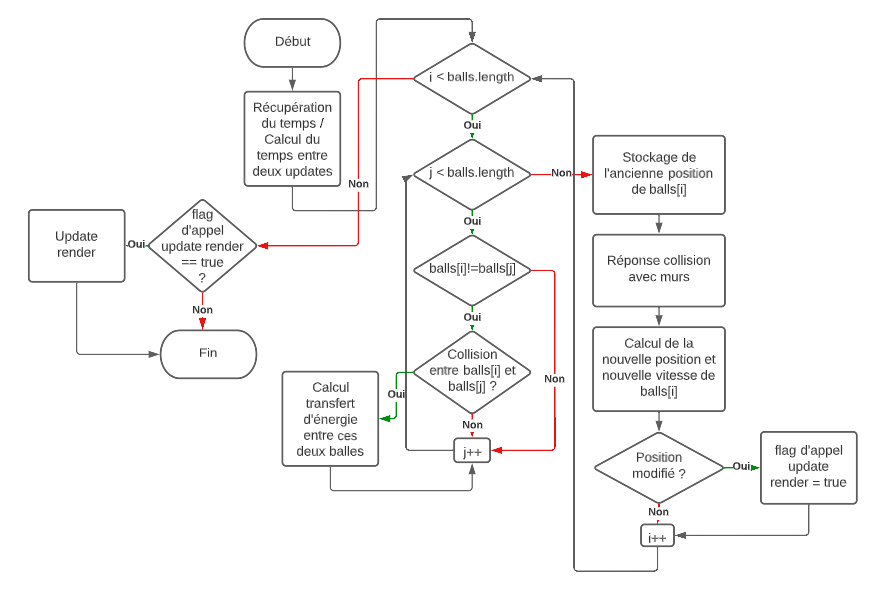
Nous avons changé la physique de notre simulation. Maintenant, on annule la modification des positions de la boule touchant une autre, de fait, on s'assure que aucune boule ne sera superposée sur une autre, voici le nouveau diagramme algorithme de la méthode BallTable.update() ainsi que le résultat :
Liens externes
Lien GitLab : lien
Cahier des charges : Fichier:P20 2022 2023 cahier des charges.pdf
Cahier des spécifications : Fichier:P20 2022 2023 cahier des spec.pdf
Rapport de mi-projet : Fichier:P20 2022 2023 rapport mitemps.pdf
Présentation mi-travail PFE du 10/11 : Fichier:P20 2022 2023 pres miPFE.pdf
Présentation PFE final : Fichier:P20 2022 2023 pres final.pdf
Rapport final : Fichier:P20 2022 2023 rapport final.pdf