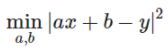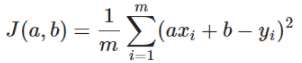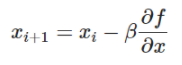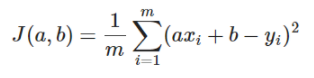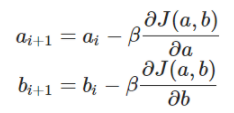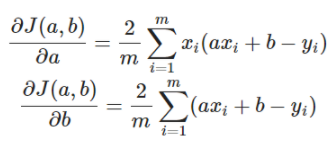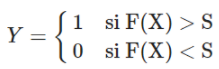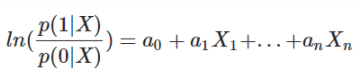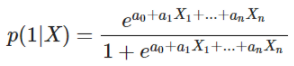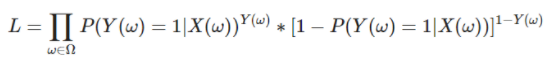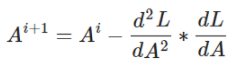IMA3/IMA4 2020/2022 P5 : Différence entre versions
(→Développement du projet) |
(→Développement du projet) |
||
| Ligne 419 : | Ligne 419 : | ||
Nous avons ensuite organisé notre projet à l’aide du diagramme de Gantt ci-dessous. | Nous avons ensuite organisé notre projet à l’aide du diagramme de Gantt ci-dessous. | ||
| − | [[Fichier:Gantt. | + | [[Fichier:Gantt.png]] |
== [[Fichier:Diagramme de Gantt]] == | == [[Fichier:Diagramme de Gantt]] == | ||
Version du 3 mai 2022 à 15:23
Sommaire
PARTIE I (S6-S7)
Introduction et cahier des charges
Introduction
L’objectif de ce projet est la mise en place d’algorithmes de machine Learning afin de diagnostiquer l’état de machines industrielles. Nous travaillerons sur ce projet durant 2 semestres. Durant le premier semestre, nous avions comme objectifs d’acquérir la maîtrise des différentes librairies primordiales pour traiter les données en machine Learning, ainsi que d’étudier et d’utiliser certains algorithmes basiques (régression linéaire, logistique, Bayes) sur des datasets que nous traiterons nous même. Pour ce qui est du second semestre, notre objectif était de concrétiser les connaissances acquises durant le premier semestre. Nous avons donc essayé de créer notre propre dataset à l’aide des matériels mis à notre disposition, de la prétraiter et d’y appliquer différents algorithmes de Machine Learning en critiquant les résultats.
Le machine Learning pour la détection de défaut s'inscrit parfaitement dans le contexte scientifique actuel, notamment grâce à l’industrie 4.0. En effet, cette nouvelle industrie fait apparaître des systèmes communicants (l’IOT : Internet Of Things) interconnectés les uns entre les autres. Ces différents systèmes peuvent êtres nécessaires les uns, les autres afin de réaliser une tâche complexe telle que l'usinage de pièces. Le système devient dès lors potentiellement extrêmement fragile aux pannes.
Le machine Learning a pour but de pouvoir détecter, et localiser les pannes, voir les futures pannes potentielles afin de pouvoir dans un premier temps prévenir un opérateur. Mais il peut aussi potentiellement permettre au système de continuer de tourner, en attendant un technicien. Le machine Learning peut donc aussi permettre à une chaîne de production de continuer de tourner par l’envoie d’un autre robot par exemple, le temps que la panne soit réparée.
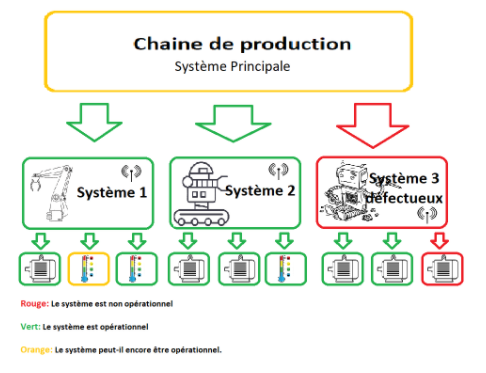
Dans le schéma ci-dessous nous avons un exemple de système de système.
Il y a deux cas de figure:
- Un autre système peut être envoyé pour remplacer le système 4.
- Les systèmes 1 et 2 peuvent permettre à la chaîne de production de continuer de tourner
- La chaîne de production est hors service jusqu'à réparation.
Cahier de charges
Ressources disponibles :
- Livres sur le machine learning
- Bases de données (afin d'appliquer divers algorithmes de machine learning) que nous prendrons sur ces sites : [1] et [2]
- Librairies Python (Scikit-learn, Pandas, Numpy, Seaborn, Matplotlib)
- Google Colab
- Matlab (version étudiante)
Objectifs poursuivis :
- Détecter les dysfonctionnements de systèmes mécatroniques (par exemple les robots Khepera, Robotino…), grâce au machine learning.
- Apprendre à implémenter différentes méthodes machine learning .
Profil du public cible :
- Secteur mécatronique
- Entreprises disposant d'ingénieurs pour maintenir le système informatique opérationnel
- Entreprises utilisant des machines dans le secteur public.
Analyse des besoins :
- L’industrie a de plus en plus besoin du machine learning pour détecter les erreurs des systèmes. En effet, cette technologie devient indispensable pour les industriels, notamment afin d'accroître la productivité et l’efficacité des systèmes industriels.
- Le programme peut ne pas être aussi rapide et optimisé en espace mémoire que d'autres programmes, nous visons l’efficacité de notre algorithme plutôt que la rapidité.
Librairies
En Machine Learning, il est très important, voire primordial, de savoir manipuler les différentes librairies mises à notre disposition afin de visualiser, traiter nos différentes dataset ou même appliquer les différents algorithmes de machine Learning. Durant les premières semaines de notre projet, nous avons donc appris à utiliser ces différentes librairies nécessaires pour le machine Learning, telles que Numpy, Seaborn, Panda, Matplotlib, Scikit-learn... Nous allons dans un premier temps nous intéresser à l'importation des différentes bibliothèques puis résumer les commandes importantes de ces différentes librairies.
Ces différentes librairies ne sont pas incluses de base dans Python, il est donc nécessaire de les ajouter à Python puis à notre programme.
Nous avons donc choisi d'utiliser google colab car ces librairies y sont déjà installées (et aussi pratique pour travailler à plusieurs sur un même code). Puis nous devons importer ces bibliothèques au début de notre programme.
Attention : Plusieurs bibliothèques peuvent avoir la même commande mais avec des significations différentes, comme par exemple la commande randint du module numpy et celle du module random et cela peut conduire à des erreurs.
Afin de pallier à ces problèmes nous apporterons nos librairie au début de nos programmes comme suit :
Ici le np permet de dire que lorsque nous utilisons np.array alors nous utilisons la commande array () contenu dans la bibliothèque Numpy.
Ceci nous permettra d’utiliser en simultané différentes librairies, toutes les bibliothèques seront importées selon ce schéma. Nous allons par la suite, nous intéresser à différentes commandes incluses dans ces librairies.
Numpy
Numpy est une bibliothèque dédiée aux calculs mathématiques et à la gestion des listes (telles que des matrices). Matplotlib, quant à lui, est dédié aux affichages graphiques de données. Nous allons dans cette partie nous intéresser aux commandes principales de ces deux bibliothèques de python.
Sous numpy, les tableaux sont des types array, ils définissent l'équivalent des tableaux statiques en langage C. La taille d’un tableau numpy ne peut donc pas être changée après leur création.
Néanmoins grâce a Numpy nous pouvons simplement effectuer des tâches sur les tableaux comme en extraire un sous tableaux, et d’effectuer simplement les produits entre matrice, vecteur.
Dans notre projet, nous utiliserons plus courament les fonctions :
- np.shape permet d’obtenir la taille de la matrice sous forme d’un tuple, suffit de choisir le bon numéro
- np.zeros permet de créer une ligne de x zéro(s)
- np.ones permet de créer une ligne de x un(s)
- np.vstack permet de rajouter des lignes dans une matrice déjà créer en paramètre
- np.transpose permet de transposer une matrice en paramètre
Seaborn
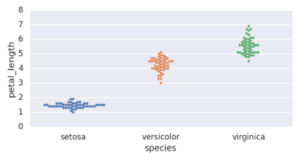
Seaborn est une bibliothèque de visualisation de données Python basée sur matplotlib. Il fournit une interface de haut niveau pour dessiner des graphiques statistiques attrayants et informatifs.
Différences entre Matplotlib et Seaborn
Les défauts de Matplotlib qui ne parlent généralement pas aux utilisateurs sont les couleurs, les marques de tiques sur les axes supérieur et droit, le style,... Les exemples ci-dessus rendent également une autre frustration des utilisateurs plus apparente: le fait que travailler avec DataFrames ne va pas aussi bien avec Matplotlib, ce qui peut être ennuyeux si vous faites une analyse exploratoire avec Pandas. Et c’est exactement ce que Seaborn adresse : les fonctions de traçage fonctionnent sur dataframes et tableaux qui contiennent tout un ensemble de données.
# Import necessary libraries
import seaborn as sns
import matplotlib.pyplot as plt
# Load iris data
iris = sns.load_dataset("iris") #DATASET ALREADY EXISTING
# Construct iris plot
sns.swarmplot(x="species", y="petal_length", data=iris)
# Show plot
plt.show()
Pandas
Pandas est une API d'analyse de données orientée colonnes. C'est un excellent outil pour manipuler et analyser des données d'entrée. Beaucoup de frameworks d'apprentissage automatique acceptent les structures de données Pandas en entrée.
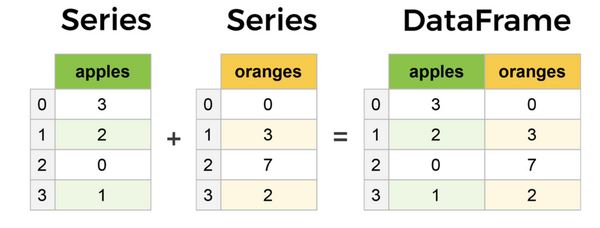
Comme évoqué précédemment, Pandas travaille avec des matrices colonnes communément appelées ‘Series’ mais aussi et surtout avec des tableaux de données appelés ‘DataFrames’. Une Series est tout simplement une colonne et une DataFrame est un tableau à plusieurs dimensions constitué de Series.
A l'aide de Pandas, on peut ainsi créer, importer, lire et manipuler des bases de données facilement.
Théories des algorithmes étudiés
Il y a différents types d’algorithmes en machine learning, pour notre sujet qui consiste à classer des machines en défectueuse ou fonctionnelles (1 ou 0), nous aurons surtout besoin d’algorithmes de classification binaire. De manière générale, la conception de la plupart des algorithmes fonctionnent de cette manière :
- Élaborer un modèle
- Établir une fonction coût pour celui-ci correspondant à l’erreur entre le modèle et les données réelles
- Trouver un algorithme de minimisation de cette fonction coût
Régression linéaire
La régression linéaire est un algorithme de prédiction et non un algorithme de classification, nous aurons surtout besoin de ce deuxième type d’algorithme pour notre projet mais nous tenons à présenter cet algorithme qui est le plus basique en machine learning et un bon début pour une formation pédagogique.
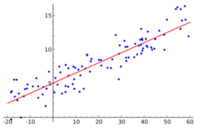
La régression linéaire est une méthode de modélisation qui cherche à établir une relation linéaire entre une ou des "features" (variables explicatives) et une "target" (variable expliquée qu'on cherche à prévoir à partir des variables explicatives). En machine learning, la régression linéaire est un modèle d'apprentissage supervisé, c'est-à-dire qu'on apprend à l'algorithme de prédiction à partir d'exemples dont on dispose dans une dataset. Nous nous intéresserons à la régression affine qui est la plus simple pour débuter.
Modèle et estimation de la fonction coût
La régression affine consiste donc à trouver un modèle de type
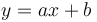
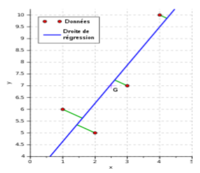
avec x une "feature", y la target et avec a et b des paramètres qu'il nous faudra déterminer. Le but est donc de trouver les paramètres a et b tels que la distance entre chaque point du nuage et la droite du modèle soit la plus petite possible. Mathématiquement, il suffit de résoudre cette formule:
On utilise donc la méthode des moindres carrés pour mesurer l'erreur entre le modèle de prédiction et les données et ainsi fabriquer notre fonction coût :
avec m le nombre de points du nuage.
L'objectif de l'algorithme est donc de trouver les paramètres optimaux qui minimisent cette fonction J. En machine learning, une des méthodes les plus populaires pour faire ceci est la descente de gradient, car c'est une méthode adaptée quand on fait du traitement de grosses dataset ("faible" temps de calcul). En effet, la fonction coût J est une parabole admettant un unique minimum dépendant des paramètres a et b. La descente de gradient consiste à chercher le point de celle-ci où la dérivée est nulle (donc le minimum)
Méthode de la descente du gradient
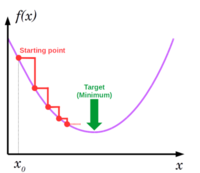
Soit une fonction parabolique ne dépendant que de x. On cherche à trouver le minimum de cette fonction en utilisant la méthode de la descente du gradient
Pour cela on choisit un point aléatoirement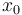 
et on va descendre à partir de celui-ci jusqu'à atteindre un minimum en utilisant
avec un paramètre qui influencera la taille du pas de la descente.
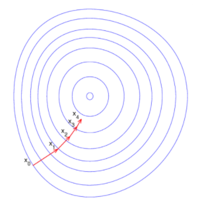
Il faut faire attention à ne pas prendre un pas trop grand, ni trop petit, pour éviter de "tourner" autour du minimum ou de prendre trop de temps pour l'atteindre. Note : On peut généraliser cela pour une fonction parabolique à n paramètres qui aurait donc une forme de bol.
Application sur notre fonction coût
Notre fonction coût dépend des 2 paramètres a et b :
On choisit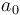 
et 
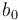aléatoirement et on applique ceci pour un pas :
Avec
Au bout d'un certain nombre d'itérations on trouve le couple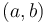 
qui minimise notre fonction coût.
Note : Nous avons démontré la théorie de la régression linéaire affine mais on pourrait généraliser celle-ci pour un modèle polynomiale d’ordre n, la courbe de prédiction serait donc parabolique et il faudrait trouver le tuple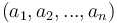 
qui minimise la fonction coût.
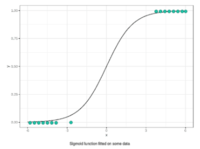
Régression logistique binaire
La régression logistique binaire est un algorithme de classification, contrairement à la régression linéaire qui est un algorithme de prédiction. De la même façon que la régression linéaire, il s'agit de modéliser au mieux un modèle mathématique simple à des observations réelles nombreuses. Cette méthode se base sur de l’analyse mathématiques et statistique. Il faut donc associer à des “features”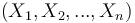 
une variable Y valant 1 ou 0 (d’où le terme classification binaire).
L’objectif de l’algorithme est donc de trouver la fonction F dépendant d’une loi de probabilité telle que :
avec S un certain seuil (fixé la plupart du temps à 0,5).
Modèle
Comme cette méthode repose principalement sur des statistiques, il est important d’adopter une notation explicite lors de l’explication théorique :
- On notera Y la variable à prédire (qui vaudra 0 ou 1) et
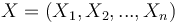les variables permettant de prédire Y - On travaillera dans un univers de N échantillons (taille de la dataset)
- On notera
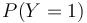et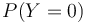 
les probabilités que Y valent respectivement 1 ou 0 
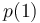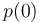
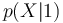et 
-
et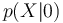 
sont les distributions conditionnelles des caractéristiques X sachant la valeur prise par Y -
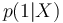et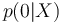 
sont donc les probabilités d’obtenir la valeur de Y (1 ou 0) sachant les valeurs de X
La régression logistique utilise l’hypothèse fondamentale (mesure de l’évidence) :
On en déduit donc (comme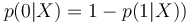 
:
Avec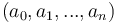 
des variables à déterminer.
Note : ce modèle est appelé modèle LOGIT.
Estimation de la fonction coût
Contrairement à la régression linéaire affine, on ne peut pas utiliser la méthode des moindres carrés, on utilise alors la méthode de maximisation de la vraisemblance. “La vraisemblance mesure une adéquation entre la distribution observée sur un échantillon aléatoire et une loi de probabilité supposée décrire une réalité sur la population dont l'échantillon est issu.” (source : [www.jybaudot.fr])
Le calcul de la vraisemblance L dans un univers de N échantillons est le suivant :
Plus la vraisemblance est élevée, alors plus la loi de probabilité est proche de la réalité. Le but est donc de maximiser cette valeur et de trouver les valeurs optimales de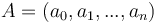 
qui influent directement sur la loi de probabilité établie dans la partie modèle.
Algorithme d'optimisation
Afin de trouver la valeur optimale du vecteur A, nous utiliserons encore une fois la méthode de descente du gradient adaptée à notre cas.
Celle-ci utilise la relation suivante :
Au bout d’un certain nombre d’itérations, on trouvera la valeur optimale de A afin de maximiser la vraisemblance.
Mise en pratique
Pour la mise en pratique, nous avons décidé d’appliquer les méthodes sur un dataset de prédiction de maintenance pour l’industrie, nous importons grâce à la librairie panda : dataset = pd.read_csv('ai4i2020.csv')
Cette dataset contient 14 colonnes de données, nous pouvons visualiser la proportion de données saines et non-saines par ce code seaborn : sns.factorplot('Machine failure',data=dataset,kind='count')
Dans un premier temps, on traitera cette dataset pour la préparer sur l’intervention des modèles de machine learning, puis on appliquera ces méthodes.
Pré-traitement de la dataset
Avant d’appliquer les algorithme sur notre dataset, il faut la traiter, le traitement sera le même pour tous les algorithmes et suivra cet ordre :
- Traitement des valeurs manquantes
- Équilibrage des données
- Séparations des données en entrainement et test
Dans un premier temps, nous devons regarder si notre base de données contient des valeurs manquante, pour cela nous implantons ce code :
import missingno as msno msno.matrix(dataset)
Les lignes blanches dans le résultat correspond aux valeurs manquantes, ci-dessous nous voyons que nous avons aucune données manquantes dans la base que nous avons importer : Fichier:Miseenpratique.png
Dans le cas, où nous avons des valeurs manquante, il y a plusieurs méthodes pour traiter les valeurs manquantes mais nous retenons 2 méthodes :
- Une méthode qui consiste à supprimer les lignes où des valeurs manquantes sont présentes :
data.dropna(inplace=True)
L’avantage de cette méthode est de créer un modèle robuste. L’inconvénient majeur est le fait qu’on peut perdre énormément de données, pour des données où les valeurs manquantes sont excessives, mieux vaut appliquer une autre méthode.
- Une méthode qui consiste à remplacer les valeurs manquantes par la moyenne des données de la colonne :
data[0]=drop[0].replace(np.NaN,data[0].mean())L’avantage de cette méthode permet d’éviter la suppression de lignes, ce qui permet de garder les autres données comparé à l’autre méthode. Cependant cette méthode n’est que applicable sur les données numériques
Nous passons alors sur l'équilibrage des données. Avant d’appliquer la méthode SMOTE, nous devons mettre dans 2 variables, la target (y) et les features (X) :
X = dataset.drop(['Machine failure','UDI','Product ID','Type','TWF','HDF','PWF','OSF','RNF'],axis=1).values y = dataset['Machine failure']
Notre target sera seulement ‘Machine failure’ et nos features seront : la température de l’air, la température du processus, le couple, et l’usure des outils.
Durant notre projet , nous avons implémenté la technique SMOTE pour traiter les ensembles de données déséquilibrées. Le principe de SMOTE est de générer de nouveaux échantillons en combinant les données de la classe minoritaire avec celles de leurs voisins proches. Techniquement, on peut décomposer SMOTE en 5 étapes :
- 1 - Choix d’un vecteur caractéristique de notre classe minoritaire que nous appellerons vc
- 2 - Sélection des k-voisins les plus proches (k=5 par défaut) et choix de l’un d’eux au hasard que l’on appellera pv
- 3 - Calcul de la différence pour chaque valeur caractéristique (feature value) i, vc[i]-pv[i] et multiplication de celle-ci par un nombre aléatoire entre [0,1]
- 4 - Ajout du résultat précédent à la valeur de la caractéristique i du vecteur vc afin d’obtenir un nouveau point (une nouvelle donnée) dans l’espace des caractéristiques
- 5 - Répétition de ces opérations pour chaque point de données de la classe minoritaire
Nous remarquons que cette technique marche après smote (50% données saines, 50% données non-saines)
Code :
oversample = SMOTE() Xsmote, ysmote = oversample.fit_resample(X,y) Xsmote = pd.DataFrame(Xsmote) ysmote = pd.DataFrame(ysmote) X=Xsmote y=ysmote
On remarque que la technique smote a ajouté 9322 lignes sur notre base, Maintenant que nous avons un équilibre entre les données ‘sains’ et ‘malsains’, nous pouvons voir la répartitions des points sur 2 axes :
(image)
Nous pouvons alors procéder à la séparation de nos données en données d'entraînement et de test
Nous devons séparer en deux nos données pour pouvoir appliquer les algorithmes de machine learning, ainsi : Les données d'entraînement serviront de repères pour l’algorithme Les données de test seront entraînées par celle d’entrainement pour créer une prédiction
Nous allons utiliser la fonction train_test_split de la librairie sklearn pour séparer nos données :
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size = 0.2, random_state = 100)
Ici dans les paramètres : X correspond aux features y correspond à la target test_size correspond au pourcentage de séparation (soit 0.2 = 20% test et 80% d'entraînement) random_state permet d’initialiser le choix aléatoire pour avoir la même répartition à chaque exécution
Maintenant nous pouvons appliquer les algorithme à notre modèle
Application des algorithmes
En général, nous allons appliquer les algorithme en suivant cet ordre :
- Importation de la méthode sur la librairie sklearn
- Entraînement des données
- Prédiction
- Méthodes d’évaluations
Régression linéaire
Nous allons commencer par le plus simple : la régression linéaire, nous commençons par importer l’algorithme à partir de la librairie sklearn : from sklearn.linear_model import LinearRegression
Puis nous appelons l’algorithme avec les paramètres de base, puis nous entraînons notre dataset :
#Méthode de régréssion linéaire lr = LinearRegression() #Training lr.fit(X_train,y_train)
Ensuite la prédiction :
#Prediction y_pred = lr.predict(X_test)
Et enfin l'évaluation, nous avons vu 2 méthodes pour évaluer notre modèle :
- Afficher le score de prédiction
- Afficher la matrice de confusion, une matrice de taille 2x2 qui donne ces informations :
Le score de prédiction (accuracy) est également calculé à partir de cette matrice Pour la régression linéaire, nous allons qu’afficher le score de prédiction, car cet algorithme nous donne en retour des valeurs non-binaire, la construction d’une matrice de confusion et impossible.
#Evaluation print(lr.score(X_test,y_test))
Nous obtenons ainsi un score de 0.48, un score qui est plus élevé sans la méthode SMOTE (0.14), sauf que cette méthode n’est pas la plus optimisée pour cette base de données, car nous avons en target des valeurs binaires. Il vaut mieux appliquer la méthode de régression logistique ou la méthode de Naives-Bayes.
Régression logistique
Dans le même modèle que la régression linéaire, nous procédons à l’import de la méthode, l’appel de la méthode, l'entraînement des données et de la prédiction :
from sklearn import linear_model
#Modèle régression logistique modele_regLog = linear_model.LogisticRegression() #random_state = 100, solver = 'liblinear', multi_class = 'auto'
#training modele_regLog.fit(X_train,y_train)
#prediction y_pred = modele_regLog.predict(X_test)
#précision du modèle precision = modele_regLog.score(X_test,y_test) print(precision)
Pour la régression logistique, nous allons afficher la matrice de confusion et le score :
from sklearn.metrics import plot_confusion_matrix plot_confusion_matrix(modele_regLog, X_test, y_test) plt.show()
(images)
Nous obtenons un score de 0.82, contre 0.97 sans la méthode de SMOTE, ce qui est cohérent car le score obtenu sans SMOTE n’est pas précis car il y avait peu de données où la machine a planté. Avec SMOTE, nous obtenons certes un score moins élevé mais plus précis. Grâce à la matrice de confusion nous pouvons voir que :
- Il y a 2396 fois où l’algorithme a prédit Machine failure = 0 et a eu raison
- Il y a 2377 fois où l’algorithme a prédit Machine failure = 1 et a eu raison
- Il y a 546 fois où l’algorithme a prédit Machine failure = 1 et a eu faux
- Il y a 478 fois où l’algorithme a prédit Machine failure = 0 et a eu faux
PARTIE II (S8)
Développement du projet
Durant les deux premiers semestres de ce projet, nous avons découvert et étudié le Machine Learning, que ce soit la théorie de différents algorithmes connus ou l'application pratique à des datasets que nous pouvons récupérer sur Internet ou bien créer nous même.
La création de notre dataset ayant été fastidieuse et peu concluante (voir résultats du semestre précédent), nous avons comme objectif pour ce semestre d'implémenter nos algorithmes (et principalement le réseau de neurones) à des machines dont nous avons accès à l'école.
Après discussion avec notre tuteur de projet Monsieur Lakhal, nous avons décidé d'utiliser des Robotino plutôt que d'utiliser la chaîne de production présente à l'école car il existe des logiciels simples permettant d'effectuer des simulations de réseaux logistiques de Robotinos (Robotino View et Robotino Simulation) dont nous allons récupérer les données en temps réel, les traiter puis commander les différents Robotino à l'aide d’un algorithme de réseaux de neurones.
L'objectif de ce semestre est ainsi de réaliser le scénario d'un réseau logistique autonome (à l'image d'Amazon par exemple) composé de plusieurs Robotino effectuant chacun une tâche et d'y introduire des erreurs puis de les traiter grâce au Machine Learning afin de ne pas perturber la logistique et d’obtenir un maximum d’efficacité.
Nous avons organisé ce projet en plusieurs étapes où chacun des membres a pu plus ou moins participé en fonction de ses capacités :
Conception du Grafcet pour la commande des Robotino
Récupération et traitement des données en temps réel
Utilisation du Machine Learning afin de commander les Robotino
Pour cela, nous avons constitué 2 équipes : une équipe spécialisée dans la commande du Robotino constituée de Loïc et Aymen et l’autre dans le traitement des données avec le Machine Learning avec Antoine, Tom et Florian.
Nous avons ensuite organisé notre projet à l’aide du diagramme de Gantt ci-dessous.
Fichier:Diagramme de Gantt
Élaboration du scénario
Traitement des erreurs
Recherche bibliographique
- Cours de probabilités et statistiques de l’Université Jules Vernes
- Chaine youtube Machine Learning : https://www.youtube.com/channel/UCmpptkXu8iIFe6kfDK5o7VQ
- Machine Learning with scikit-learn Quick Start Guide écrit par Kevin Jolly
- Machine Learning algorithms - Second Edition écrit par Giuseppe Bonaccorso
