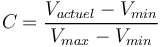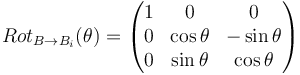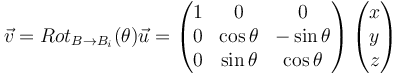Projet IMA3 P3, 2017/2018, TD2 : Différence entre versions

De Wiki de Projets IMA
(→‎Contraste)
(→‎Application de rotations sur un vecteur en trois dimensions)
Ligne 137 : Ligne 137 :
  
 
== Application de rotations sur un vecteur en trois dimensions ==
 
== Application de rotations sur un vecteur en trois dimensions ==
 +
 +
Soit <math>\vec{u} = \left ( \begin{matrix} x \\ y \\ z \end{matrix} \right )</math>, un vecteur de dimension 3 dans une base canonique <math>B = \{O; \vec{i}, \vec{j}, \vec{k}\}</math> de dimension 3.
 +
 +
Soit <math>B_i = \{O; \vec{i}, \vec{j'}, \vec{k'}\}</math>, une autre base canonique tournée d'un angle <math>\theta</math> autour de l'axe <math>\vec{i}</math> par rapport à la base <math>B</math>.
 +
 +
Alors la matrice de rotation <math>Rot_{B \rightarrow B_i}(\theta) \in M_{3, 3}(\mathbb{R})</math> est définit comme :
 +
 +
::<math>Rot_{B \rightarrow B_i}(\theta) = \left ( \begin{matrix} 1 & 0 & 0 \\ 0 & \cos{\theta} & -\sin{\theta} \\ 0 & \sin{\theta} & \cos{\theta} \end{matrix} \right )</math>
 +
 +
Le vecteur <math>\vec{u}</math> écrit dans la base <math>B_i</math>, noté <math>\vec{v}</math>, est alors :
 +
 +
::<math>\vec{v} = Rot_{B \rightarrow B_i}(\theta) \vec{u} = \left ( \begin{matrix} 1 & 0 & 0 \\ 0 & \cos{\theta} & -\sin{\theta} \\ 0 & \sin{\theta} & \cos{\theta} \end{matrix} \right ) \left ( \begin{matrix} x \\ y \\ z \end{matrix} \right )</math>
 +
 +
Cette opération peut être reproduite plusieurs fois à la suite en changeant les axes de rotation pour obtenir le repère décrit pour le moteur graphique.
  
 
== Projection en perspective ==
 
== Projection en perspective ==

Version du 15 juin 2018 à 18:30

Voici le wiki du projet SC IMA3 de l'équipe TD2 P3 composée de Yanzhe Tan, Xinwei Hu et Pierre Frison pour l'année 2018.

Projet informatique

Cahier des charges

Construire une caméra 5x5 pixels grâce à des photorésistances. Nous ferons la démonstration de l'utilité d'un tel système :

  • Simple visionnage en 2 dimensions
  • Visionnage du profil d'un objet en 3 dimensions
  • Contrôle de divers systèmes (exemple avec un contrôleur audio pour Android)

Matériel nécessaire

  • 25 photo-resistances
  • 25 résitances 2 kOhm
  • 25 transistors NPN (2n2222 ou équivalent)
  • 5 résistances 820 Ohm
  • 1 Arduino
  • 1 Raspberry PI 3

Communication série

Pour réaliser la communication entre l'Arduino et la raspberry pi, nous avons choisi la liaison en série avec un câble USB. L'Arduino va lire les valeurs via des photorésistances et les sauvegarder dans une chaîne de caractères dans la forme "xxx-xxx-xxx-xxx-...". Ensuite, l'Arduino envoie la chaîne à la raspberry pi, en même temps de réception, nous découpons la chaîne de caractères entre 25 petites chaînes de caractères,en utilisant la fonction "stringObject.substring(start, stop)", et les transformons entre 25 numbres en décimal stockés dans un tableau 5x5. Dans cette processus, nous déterminons aussi les valeurs maximale et minimum, avec les quelles nous pouvons calculer le pourcentage du niveau de gris. Et à la fin, nous allons afficher 25 blocs en 5x5 avec des gris de différentes niveau selon la détection de l'Arduino.

Visionnage en deux dimensions

Visionnage en trois dimensions

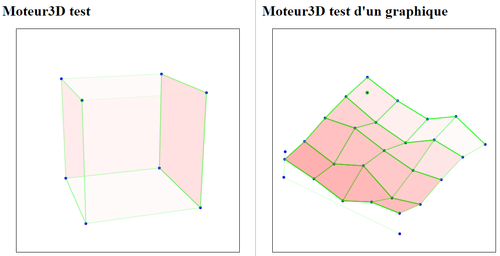
Tests du moteur 3D avec un cube (à gauche) et un graphique représentant à quoi devrait ressembler un graphique dans sa version finale (à droite) (fichiers disponible sur le Github du groupe)

Notre but ici est de visionner le profil de l'objet grâce à l'ombre qu'il produit lorsqu'il est devant la caméra. Il nous a donc donc fallu dans un premier temps réaliser un moteur graphique en trois dimension (le plus basique possible) pour afficher le résultat.

Les données envoyées au moteur pour le rendu sont :

  • une liste de points avec trois dimensions
  • une liste de lignes avec 2 points par ligne
  • une liste de polygones avec trois ou plus points par polygone.
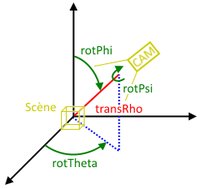
Cette image illustre les angles et la translation que réalise le moteur graphique

Pour le rendu, le script en Javascript applique trois transformations angulaires correspondant aux deux angles du repère sphérique, plus une autre rotation autour de l'axe de la caméra. Les trois rotations sont appelées : rotTheta, rotPhi, rotPsi.

Le script applique ensuite une translation des points suivant l'axe de la caméra. translation appelée transRho.

Notre scène est toujours en trois dimensions et ne peut pas être affichée sur un écran qui n'a que deux dimensions. Le script va alors réaliser une projection en perspective (une simple division : plus le point est loin de la caméra plus il sera proche du centre). Cette projection tiens comptes d'une distance appelée tirageMecanique qui est la distance entre l'écran et le point de perspective.

Une fois les coordonnées X et Y des points projetés sur l'écran, le moteur dessine les points, les lignes et les polygones sur l'écran.

En répétant l'opération régulièrement et en modifiant les coordonnées des points ou les angles ou la distance de la caméra à la scène, on obtient une animation.

Les codes sources (fichiers HTML avec du Javascript) sont disponibles sur le Github du groupe.

Contrôleur audio Android

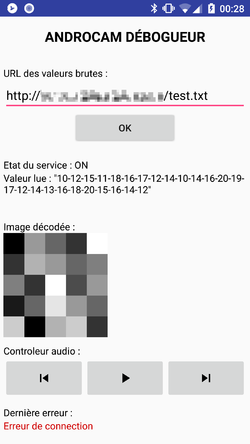
Ecran de débogage de l'application Android (application et sources disponible sur le Github du groupe)

La caméra pourrait servir à contrôler divers appareils. Pour en faire la démonstration, nous nous somme aventuré à la création d'une application Android qui serait capable de lire des données affichées sur une page web générée par la Raspberry et d'interpréter ces données en commande pour le lecteur audio d'Android.

Nous avons pensé à trois commandes basiques :

  • lecture et pause lorsqu'un objet (une main par exemple) obscurcit brièvement la vision au centre de la caméra
  • lecture de la chanson suivante lorsqu'un objet obscurcit la caméra de la gauche vers la droite
  • lecture de la chanson précédente lorsqu'un objet obscurcit la caméra de la droite vers la gauche

L'application démarre sur un panneau de débogage, unique écran (Activity) de l'application, le reste étant géré dans un processus en arrière-plan (Service). Dans le premier champ, il faut y entrer l'URL où Android pourra récupérer les informations brutes sur le serveur web de la Raspberry. Si l'application arrive à se connecter, elle affichera dans l'écran de débogage diverses informations : valeurs lues en brute, image reconstituée, etc.

Une fois l'application ouverte, l'utilisateur peut la "fermer" : la fermeture "normale" (différente de la fermeture forcée dans le gestionnaire des applications) détruit simplement l'Activity (l'écran de débogage) et non le Service qui va continuer à interroger la Raspberry et à contrôler le lecteur audio.

Comme énoncé précédemment, le Service est une tâche exécutée en fond qui s'occupe du téléchargement des données brutes, de l'interprétation de l'image (non différente des autres systèmes, c'est à dire un calcul de contraste) et du contrôle du lecteur audio d'Android.

Le code source et l'APK compilé sont disponibles sur le Github du groupe.

Activité électronique

Conception du circuit imprimé

Détail d'une cellule
Schematic final du circuit imprimé
Le circuit imprimé avec tous les composants soudés

La partie électronique sera un quadrillage de 25 photorésistances avec une carte Arduino pour récupérer les informations et les transmettre à la partie informatique. L'Arduino affichera aussi l'image reconstituée sur une matrice de LED.

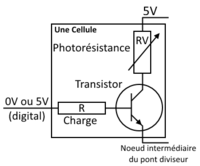
Ce schéma électrique (appelé cellule) sera le même pour les 25 photorésistances de notre quadrillage. Le transistor permet au courant de circuler ou non entre l'alimentation et le noeud intermédiaire du pont diviseur de tension. Si la tension à la base du transistor (la résistance R est ici pour délivrer du courant à la base) est de 5V (niveau logique haut) le courant passe (le courant est bloqué dans le cas 0V).

Chaque colonnes sont connectés avec un pont diviseur de tension. Ce pont diviseur de tension permet à la tension au milieu du noeud d'être seulement fonction de la valeur de la photorésistance (les autres valeurs étant constantes). Il suffit maintenant de transformer cette tension en valeur binaire grâce à un convertisseur analogique-numérique et d'envoyer le résultat à la partie informatique.

Bien sûr, il nous faut commander chaque ligne pour autoriser ou non le passage du courant (principe du rolling shutter). Il faut autoriser le passage du courant dans une seule ligne et passer à la suivante dès que le convertisseur analogique-numérique a obtenu les valeurs de la ligne précédente.

Programmation de l'Arduino

La carte Arduino est utilisée pour récupérer les valeurs de photorésistance par le biais de ponts diviseurs connectés à chacune de ces entrées analogiques. La tension à une entrée analogique est donc fonction de et uniquement de la valeur des photorésistances.

Pour relier plusieurs capteurs, il nous a fallu utiliser un multiplexage réalisé avec des transistors. Ainsi, 5 capteurs sont branchés en parallèle et les ports digitaux de l'Arduino permettent de contrôler le passage du courant dans chaque capteur.

Le premier programme "Camera_test" nous a servi de tester notre carte électronique. Il transmet une visualisation avec des caractères ASCII de l'image reconstituée par l'Arduino. Le texte ASCII représentant l'image est envoyé à l'ordinateur par liaison série. Pour une meilleure visualisation, la programme ajuste le contraste de l'image : il définit le pixel le plus clair comme la valeur la plus haute enregistré depuis le lancement du programme (réciproquement, le noir correspond à la valeur la plus basse depuis le lancement).

Le second programme "Camera_serial" envoie les informations brutes des capteurs. Ce sera à la Raspberry ou tout autre appareil branché au port série de faire son propre calcul du contraste. Les informations sont envoyées selon le format suivant (toutes les valeurs (captXX) sont des entiers de 0 à 1024) : 

   capt00-capt01-capt02-capt03-capt04-capt10-capt11-...-capt44   //image à t = 0
   capt00-capt01-capt02-capt03-capt04-capt10-capt11-...-capt44   //image à t = 1
   capt00-capt01-capt02-capt03-capt04-capt10-capt11-...-capt44   //image à t = 2

Les codes sources (fichiers Arduino) sont disponibles sur le Github du groupe.

Difficulté rencontrée

Lors de nos tests finaux sur le produit fini (circuit imprimé + Arduino programmé), nous avons été déçus que la caméra ne fonctionnait pas correctement. En effet le montage ne fonctionne que si nous passons notre main de manière latérale (droite et gauche) et non longitudinalement (avant et arrière).

Nous avons rapidement déterminé que le multiplexage avec les transistors était en cause. Le montage fonctionnait pourtant en laboratoire avec un générateur de signaux. Après avoir mesuré diverses tensions au multimètre directement sur le circuit imprimé en fonctionnement, nous nous sommes aperçu que l'Arduino délivrait une tension de 0.05 volts à ses ports digitaux en guise de signal "LOW". Ce voltage qui nous paraissait infime au départ, est devenu notre suspect numéro un après avoir un rapide calcul : les ports digitaux étant reliés à des résistances puis aux bases des transistors, nous avons calculé que 0.05V provoquerait, à cause de la résistance, un courant de l'ordre de la dizaine de microamprère. Nous pensons que ce courant est suffisant pour laisser libre passage au courant entre le collecteur et l'émetteur des transistors.

Il était malheureusement trop tard pour régler ce problème mais nous avons quelques pistes pour le régler ou le contourner :

  • Remplacer la carte Arduino par un autre type de carte
  • Ajouter des circuits entre les ports digitaux et les bases des transistors qui délivreraient une tension de 0 volt ou légèrement négatif (un montage comparateur avec un amplificateur opérationnel par exemple)
  • Augmenter la valeur des résistances aux bases des transistors pour induire un courant moins important

Notions mathématiques utilisées

Certaines notions mathématiques non vu en cours qui sont redondantes dans ce wiki ou qui demande une explication particulière sont recensées ici.

Contraste

Notre calcul du contraste est réalisé à chaque réception des informations selon la formule suivante :

C = \frac{V_{actuel} - V_{min}}{V_{max} - V_{min}}

avec :

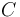  • C, la valeur du contraste. Valeur compris entre 0 et 1 inclus.
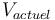  • V_{actuel}, la valeur brute reçue.
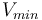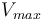  • V_{min} et V_{max}, le minimum et le maximum parmis toutes les valeurs brutes reçues depuis le début des calculs.

Ce calcul nous permet de réaliser le calibrage automatiquement. Car en effet les ponts diviseurs de tension ne pourront jamais nous donner les valeurs minimales (0 volt) et maximum (5 volts) car les valeurs des photorésistances varient seulement de 300 Ohms à 2 kOhms.

Application de rotations sur un vecteur en trois dimensions

Soit 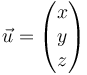\vec{u} = \left ( \begin{matrix} x \\ y \\ z \end{matrix} \right ), un vecteur de dimension 3 dans une base canonique 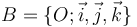B = \{O; \vec{i}, \vec{j}, \vec{k}\} de dimension 3.

Soit 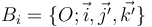B_i = \{O; \vec{i}, \vec{j'}, \vec{k'}\}, une autre base canonique tournée d'un angle 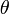\theta autour de l'axe 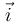\vec{i} par rapport à la base B.

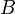Alors la matrice de rotation 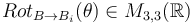Rot_{B \rightarrow B_i}(\theta) \in M_{3, 3}(\mathbb{R}) est définit comme :

Rot_{B \rightarrow B_i}(\theta) = \left ( \begin{matrix} 1 & 0 & 0 \\ 0 & \cos{\theta} & -\sin{\theta} \\ 0 & \sin{\theta} & \cos{\theta} \end{matrix} \right )

Le vecteur 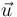\vec{u} écrit dans la base 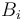B_i, noté 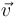\vec{v}, est alors :

\vec{v} = Rot_{B \rightarrow B_i}(\theta) \vec{u} = \left ( \begin{matrix} 1 & 0 & 0 \\ 0 & \cos{\theta} & -\sin{\theta} \\ 0 & \sin{\theta} & \cos{\theta} \end{matrix} \right ) \left ( \begin{matrix} x \\ y \\ z \end{matrix} \right )

Cette opération peut être reproduite plusieurs fois à la suite en changeant les axes de rotation pour obtenir le repère décrit pour le moteur graphique.

Projection en perspective

Récupérée de « https://projets-ima.plil.fr/mediawiki/index.php?title=Projet_IMA3_P3,_2017/2018,_TD2&oldid=58699 »