InitRech 2015/2016, sujet 1 : Différence entre versions
(→Summary) |
(→Summary) |
||
| Ligne 6 : | Ligne 6 : | ||
So, in first the author insist on the difficulty to anticipate the movement because of the infinite number of degrees of freedom, and also on the several advances made on this subject by other scientists.<br /> But to control a soft robot he explains that we need a real-time computation and thanks to algorithms adapted to GPU, the computation time can be reduced. | So, in first the author insist on the difficulty to anticipate the movement because of the infinite number of degrees of freedom, and also on the several advances made on this subject by other scientists.<br /> But to control a soft robot he explains that we need a real-time computation and thanks to algorithms adapted to GPU, the computation time can be reduced. | ||
<br /><br /> | <br /><br /> | ||
| − | |||
After that he explains the principle of the FEM. Before everything he needed to know the constitutive law of the soft material by making stress-strain response under tension experiments and he found with a linear regression that the strain/stress ratio is approximatively linear that will reduce the time of online execution of the FEM. | After that he explains the principle of the FEM. Before everything he needed to know the constitutive law of the soft material by making stress-strain response under tension experiments and he found with a linear regression that the strain/stress ratio is approximatively linear that will reduce the time of online execution of the FEM. | ||
| − | But when he assembled the possible rotation in the model is no more linear but it's still possible to compute it with an C++ implementation thanks to the open-source framework SOFA. | + | But when he assembled the possible rotation in the model is no more linear but it's still possible to compute it with an C++ implementation thanks to the open-source framework SOFA. To have the FEM model we need to compute the following linearization of the internal forces :<br /> |
| + | f(xi) ≈ f(xi−1) + K(xi−1)(xi − xi−1)<br /> | ||
| + | Where f is the volumetric internal stiffness forces and K the tangent stiffness matrix that we can deduct with static equilibrium :<br/> | ||
| + | −K(xi−1)dx = p + f(xi−1) + (J^T)*λ <br/> | ||
| + | with p is the gravity and (J^T)*λ the contribution of actuators and contact forces.<br/> | ||
| + | But, in addition of the FEM we add a new method that refer new directions in the (J^T) matrix and after that we have to resolve the structure with λ = 0 to find <math>x_{free}</math> that is a free configuration of the robot. | ||
| + | <br/>The next step is to find λ by using the constraint-based solver that allow us to find the final configuration :<br/> | ||
| + | xt = xfree + K^(−1) * J^T * λ. | ||
= Main contribution = | = Main contribution = | ||
= Applications = | = Applications = | ||
Version du 10 juin 2016 à 21:24
Summary
This article deals with the benefits of using elastic soft Robots. For now, the approaches to create them are made by inspiration from nature but with their high elasticity it's really hard to control them.
So it's necessary to know how to modelize their movement and that's what the article explain with the Finite Element Method ( FEM ) in order to model the deformations that are the cause of a mechanical coupling.
So, in first the author insist on the difficulty to anticipate the movement because of the infinite number of degrees of freedom, and also on the several advances made on this subject by other scientists.
But to control a soft robot he explains that we need a real-time computation and thanks to algorithms adapted to GPU, the computation time can be reduced.
After that he explains the principle of the FEM. Before everything he needed to know the constitutive law of the soft material by making stress-strain response under tension experiments and he found with a linear regression that the strain/stress ratio is approximatively linear that will reduce the time of online execution of the FEM.
But when he assembled the possible rotation in the model is no more linear but it's still possible to compute it with an C++ implementation thanks to the open-source framework SOFA. To have the FEM model we need to compute the following linearization of the internal forces :
f(xi) ≈ f(xi−1) + K(xi−1)(xi − xi−1)
Where f is the volumetric internal stiffness forces and K the tangent stiffness matrix that we can deduct with static equilibrium :
−K(xi−1)dx = p + f(xi−1) + (J^T)*λ
with p is the gravity and (J^T)*λ the contribution of actuators and contact forces.
But, in addition of the FEM we add a new method that refer new directions in the (J^T) matrix and after that we have to resolve the structure with λ = 0 to find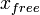 
that is a free configuration of the robot.
The next step is to find λ by using the constraint-based solver that allow us to find the final configuration :
xt = xfree + K^(−1) * J^T * λ.
