P5 Filtrage des indicateurs numériques de diagnostic : Différence entre versions
(→Traitement de signal) |
(→Traitement de signal) |
||
| Ligne 47 : | Ligne 47 : | ||
En terme de fonction de transfert (en z), on obtient donc la fonction suivante : [[Fichier:Fct_transfert.png|280px|]] | En terme de fonction de transfert (en z), on obtient donc la fonction suivante : [[Fichier:Fct_transfert.png|280px|]] | ||
| + | |||
| + | La réponse fréquentielle de ce filtre est donc : [[Fichier:Rep_freq.png|240px|]] | ||
| + | |||
| + | Ce qui est une réponse fréquentielle d'un filtre passe-bas, et ce qui nous aidera donc à éliminer les bruits comme on l'a cité de façon empirique plus haut. | ||
| Ligne 56 : | Ligne 60 : | ||
Le signal dans ce cas la se trouve alors bruité du fait de la faible précision du capteur. Dans ce cas la le bruit est d'une fréquence assez faible ce qui rend l'utilisation de la moyenne glissante assez peu utile. Etant donné la puissance de ce type de filtre, et le faible signal obtenue lors des petites fuites, la moyenne glissante risque d'effacer le signal recherché en essayant de filtrer ce dernier. | Le signal dans ce cas la se trouve alors bruité du fait de la faible précision du capteur. Dans ce cas la le bruit est d'une fréquence assez faible ce qui rend l'utilisation de la moyenne glissante assez peu utile. Etant donné la puissance de ce type de filtre, et le faible signal obtenue lors des petites fuites, la moyenne glissante risque d'effacer le signal recherché en essayant de filtrer ce dernier. | ||
| + | |||
| + | Malgré l'efficacité de la moyenne glissante, le problème de repliement spectral se pose néanmoins. Car vu la courbe de la réponse fréquentielle (cf : courbe ci-dessous), certains signaux ne sont absolument pas filtrés (gain 0dB). Ce qui explique la présence de certains bruits qui n'ont pas été éliminés. | ||
| + | |||
| + | [[Fichier:Rép_freq_courbe.png |alt=Réponse fréquentielle de la moyenne glissante]] | ||
Version du 6 décembre 2014 à 00:03
Sommaire
Introduction
Présentation du système
Notre travail se réalise, sur un générateur de vapeur couramment appelé GV, qui est l’une des composantes principales des réseaux électriques thermiques et nucléaires. Le principe de fonctionnement d’un générateur de vapeur est de pomper une eau à température ambiante d’un réservoir et de la porter ébullition à haute pression. Une fois cette eau portée à ébullition, la vapeur commence à s’échapper sous pression et fait tourner le groupe turbo-alternateur, qui se compose d’une turbine couplée à un alternateur.
Le système se compose donc de :
• Un réservoir qui contient une eau à température ambiante
• Des pompes pour pomper l’eau du réservoir
• Une chaudière pour porter l’eau à ébullition
• Le groupe turbo-alternateur
Travail à réaliser
Tout procédé industriel nécessitant une supervision logicielle, cette dernière est effectuée pour notre système sous Matlab/Simulink ainsi que dSpace. Cette supervision se base sur les données recueillis à partir des capteurs implantés sur le système, pour prévenir d'un dysfonctionnement ou d'un problème.
[interface de supervision]
Malheureusement les signaux envoyés par les capteurs sont bruités, et la dérivation numérique de ces signaux-là ne fait qu'empirer les choses. Dans le cadre de notre PFE, on essaiera de filtrer ces bruits-là, et donc de rendre la détection de défauts plus fiable et efficace.
Problématique
Le principe de la supervision et la détection d'erreur a partir des équations régissant le fonctionnement du système. Les anomalies détectées au niveaux de ces équations est ce qu'on appelle des erreurs. Les erreurs sont calculées a partir des variables composants les équations suivies ou surveillées. En vue du fait que la supervision effectué sur ce système se base sur les valeurs des différentes grandeurs physiques, l'utilisation de capteur joue un rôle primordial dans notre étude ainsi le traitement des signaux obtenue constitue une grande partie de notre travail.
Traitement de signal
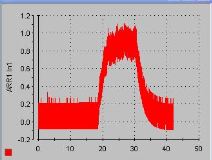
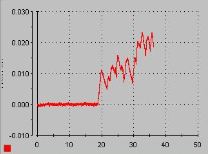
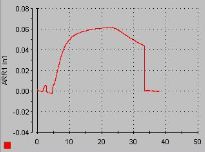
On peut voir sur les images que les signaux obtenue sont difficilement utilisable dans le cadre d'une supervision optimal. Le but de la supervision étant la détection d'un front montant au niveau des erreurs, le bruit observé sur les signaux obtenue prouve bien l'impossibilité de l'application de cette tache.
Un filtrage est indispensable pour le bon fonctionnement du système de supervision. Les filtres de première ordre étant obsolète pour un bruit d'une telle envergure, le moyen le plus utilisé dans ce cas la est l'utilisation d'un moyennage statistique supprimant les fluctuations transitoires de façon à en souligner les tendances à plus long terme. Le moyenneur le plus efficace et le plus utilisé est ce qu'on appelle une moyenne glissante. Cette moyenne est dite mobile parce qu'elle est recalculée de façon continue, en utilisant à chaque calcul un sous-ensemble d'éléments dans lequel un nouvel élément remplace le plus ancien ou s'ajoute au sous-ensemble.
Plus exactement et de manière plus mathématiques et moins empirique, la moyenne glissante est un filtre numérique avec des coefficients qui peuvent être identiques ou pas, selon notre besoin. Dans le cas de coefficients on donne la même importance à tous les échantillons, mais dans le cas de coefficients différents on accorde une importance différente à chacun des échantillons. L'utilisation de l'un ou de l'autre diffère selon le besoin, dans notre cas on accordera la même importance à tous les échantillons et donc on utilisera une moyenne glissante à coefficients égaux.
On choisira donc comme coefficient : 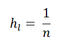
La valeur donc de la kième valeur est donc : 
En terme de fonction de transfert (en z), on obtient donc la fonction suivante : 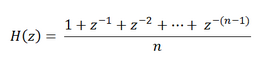
La réponse fréquentielle de ce filtre est donc : 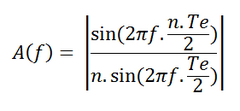
Ce qui est une réponse fréquentielle d'un filtre passe-bas, et ce qui nous aidera donc à éliminer les bruits comme on l'a cité de façon empirique plus haut.
Le résultat obtenue est assez extraordinaire, en vue de l'envergure du bruit on a choisit d'utiliser deux moyenne glissante ce qui rend le filtrage plus efficace comme expliqué auparavant. On voit sur l'image que le signal est plus lisse et donc mieux adapté a la détection des erreurs.
Lors des essaies effectués on a remarqué que par exemple pour une fuite assez faible le capteur a du mal a détecter la bonne valeur du niveau d'eau dans le réservoir variant au tour d'une certain valeur ce qui implique une variation de l'erreur en cas d'une faible fuite.
Le signal dans ce cas la se trouve alors bruité du fait de la faible précision du capteur. Dans ce cas la le bruit est d'une fréquence assez faible ce qui rend l'utilisation de la moyenne glissante assez peu utile. Etant donné la puissance de ce type de filtre, et le faible signal obtenue lors des petites fuites, la moyenne glissante risque d'effacer le signal recherché en essayant de filtrer ce dernier.
Malgré l'efficacité de la moyenne glissante, le problème de repliement spectral se pose néanmoins. Car vu la courbe de la réponse fréquentielle (cf : courbe ci-dessous), certains signaux ne sont absolument pas filtrés (gain 0dB). Ce qui explique la présence de certains bruits qui n'ont pas été éliminés.
Pour palier a ce problème, on a créer un moyenneur assez ressemblant a la moyenne glissante, utilisant le bock simulink "mean" donnant la moyenne des valeur obtenue a chaque front montant. La moyenne étant contrôler par un signal extérieur le but du travail est de trouvé le signal permettant d'avoir un signal exploitable.
Il est possible d'utiliser un signal carre qui nous permettra de définir une certaine durée ( la période du bruit) avant calcul de la moyenne. En vue de la non-homogénéité du bruit, fréquentiellement parlant, le signal carrée peut être une solution au problème mais non la plus adapté.
Le signal approprié a la commande du moyenneur est le signal lui même. En vue de la faible fréquence du signal il est possible d'utilisé ce dernier pour notre commande. Cela se résume en un calcul de la moyenne entre deux front montant du signal ce qui permettra avoir la moyenne de chaque variation du signal est donc avoir un bon fonctionnement du filtre étant donné que celui-ci s'adapte a n'importe quel type de signal étant donnée qu'on utilise le signal même, contrairement a l'utilisation d'un signal carrée qui reste fixe quelques soit le signal a filtré.
Détection du niveau d'erreur
La détection d'erreur étant faite ainsi que le traitement du signal , la deuxième partie de notre travail consiste a déterminer le niveau de l'erreur. Pour mieux comprendre le problème, l’exemple d'une fuite dans un réservoir est l'exemple parfait mais aussi la première partie de notre travail. Certes notre système de supervision permet la détection de n'importe quel fuite même la plus petite. Il est intéressant de déterminer le niveau de la fuite au niveau du réservoir. Plus la fuite est grande plus l'erreur le sera, le but de notre travail et de déterminer des paliers d'erreur permettant de connaitre le niveau de l'erreur.
La premier partie consiste a modéliser les niveaux de fuite possible sous la forme d’équation a implémenter au niveau de notre système de supervision.