Contrôle de sonar, 2012/2013, TD2 : Différence entre versions

Version du 6 juin 2013 à 10:28 (voir la source) Shaddaou (discussion | contributions) (→‎Partie Electronique) ← Modification précédente		Version du 6 juin 2013 à 11:01 (voir la source) Shaddaou (discussion | contributions) (→‎Partie Electronique) Modification suivante →
Ligne 321 :		Ligne 321 :
	Ici :		Ici :
		+
		+	<math>\dfrac{V_s}{V_reception}=1+\dfrac{R_2}{R_1}</math>
		+
		+
		+
		+	Afin d’avoir un gain de 100, on prend comme valeur R1 = 200 &Omega et R2 = 20 k &Omega. Un tel gain n’est peut-être pas obtenable avec un seule AOP, dans ce cas, il suffit de placer deux AOPs en cascade afin d’obtenir le gain espéré.
		+
		+
		+	====Filtrage du signal reçu====
		+
		+
		+	Le signal sera filtré de la même manière que le filtrage réalisé sur l’émission, on réalise ainsi le circuit de filtrage suivant :
		+
		+
		+
		+	[[Image:Imgx.PNG|center|alt=Altium7]]
		+
		+
		+	<math> G=G_1+G_2 = 20\log\right(\dfrac{1}{\sqrt{1+(R_1\times C_1\times\Omega}^{2}}\left) = 20\log\right(\dfrac{1}{\sqrt{1+\right(\dfrac{1}{R_1\times C_1\times\Omega}\left)^{2}}\left)</math>
		+
		+
		+
		+	Il faut alors déterminer <math>R_1</math>, <math>C_1</math>, <math>R_2</math>, <math>C_2</math> afin d’avoir une bande passante de gain maximum à la fréquence <math>f_0 = 40 kHz</math>.
		+
		+
		+	Enfin, on vient placer un comparateur à seuil à la sortie du filtre, ainsi lors de le signal dépassera une certaine valeur, la sortie du comparateur passera à 1 signifiant qu’une réception a eu lieu.
		+
		+
		+	====Pour aller plus loin=====
		+
		+
		+
		+	La solution précédente n’est en réalité pas applicable vu le cout qu’elle représenterait à fabriquer.
		+
		+	Nous allons donc vous proposer une solution entièrement analogique qui ne nécessite pas l’intervention d’une puce FPGA.
		+
		+	Cette partie fut en partie réalisée, mais cependant, de part des problèmes survenus lors de son élaboration, l’intégralité ne fut réalisée.
		+
		+
		+
		+	======Simulation de la Nanobord et partie émission======
		+
		+	Afin d’établir une fréquence de 40 kHz, qui est normalement donné en sortie de la Nanobord, on utilise un circuit analogique.
		+
		+	Ainsi, à l’aide de deux portes « Nand », on va reproduire un oscillateur de 40 kHz et de rapport cyclique de 0.5. On réalise alors le schéma suivant :
		+
		+
		+	Le FPGA (Nanoboard) prenant le relais par la suite, cette partie est alors terminée.
		+
		+
		+
		+	[[Image:Imgx.PNG|center|alt=Altium7]]
		+
		+	Dont la fréquence est définie par :
		+
		+	<math>f=\dfrac{1}{2.2\times(R_5+P_1)\times C_2}</math>
		+
		+	Ainsi, si l’on veut obtenir une fréquence de 40 kHz, on doit trouver les valeurs des composants de valeurs ci-dessous.
		+
		+	<math>R_4=1M\Omega</math>
		+	<math>R_5=470\Omega</math>
		+	<math>P_1=4.7k\Omega</math>
		+	<math>C_2=4.7nF</math>
		+
		+	On est alors censé obtenir un oscillateur de rapport cyclique constant égal à 0.5 et de fréquence 40 kHz. Cependant lors de sa réalisation, seul du bruit est visible en sortie (nous sommes donc bloqué ici dans la réalisation).
		+
		+	Aussi, nous souhaitons émettre des « slaves » d’émission de 10 périodes toutes les 25,5 ms. Nous allons donc réaliser ce principe grâce à un circuit permettant de réaliser une horloge de fréquence et rapport cyclique variable : un NE555.
		+
		+	<math>f=\dfrac{1.44}{(R_1+R_2\times 2)\times C_1}</math>
		+
		+
		+	<math>D=\dfrac{R_2}{2R_2+R_1}</math>
		+
		+
		+	Ainsi, à l’aide des deux équations données dans la documentation constructeur et pour un rapport cyclique de 0.99 et une fréquence de 38 Hz, on obtient les valeurs des composants suivantes :
		+
		+	<math>R_1=80k\Omega</math>
		+	<math>R_2=820\Omega</math>
		+
		+
		+	<math>C_1</math> prenant pour valeur par défaut 470 nF.
		+
		+	Ces valeurs de composant n’étant pas forcement normalisées ou disponibles, on place sur le circuit les valeurs suivantes :
		+
		+	<math>D=\dfrac{820+80\times 10^{3}}{80\times 10^{3} +2.820}=0.99</math>
		+
		+
		+	<math> f=\dfrac{1}{(80\times 10^{3} +2.820)\times 470\times 10^{-9}}=37.52 Hz</math>
		+
		+	Les oscillogrammes capturés confirment le résultat attendu :
		+
		+	[[Image:Imgx.PNG|center|alt=Altium7]]
		+
		+	[[Image:Imgx.PNG|center|alt=Altium7]]
		+
		+	[[Image:Imgx.PNG|center|alt=Altium7]]
		+
		+	Afin de pouvoir générer 10 périodes à 40 kHz, on inverse le signal en sortie du NE555 (à l’aide d’une NAND), on obtient donc :
		+
		+	[[Image:Imgx.PNG|center|alt=Altium7]]
		+
		+	Ainsi, en établissant un ET logique entre cette tension et celle de l’oscillateur à 40 kHz, on permet l’envoie d’une slave (10 périodes à 40 kHz) à l’émetteur.
		+
		+	Nous sommes alors censés obtenir la tension désirée représentant la tension de sortie de la Nanobord qui est ensuite envoyé au montage permettant la création d’un signal alternatif de ±5V.
		+
		+
		+
		+	=====Partie réception=====
		+
		+	La partie réception quant à elle ne change pas par rapport à la solution impliquant la puce FPGA, c’est-à-dire que l’on effectue une amplification puis un filtre sur le signal reçu.
		+
		+
		+	====Conclusion====

---

Version du 6 juin 2013 à 11:01

Evaluation informatique et électronique

Gestion de projet / rédaction Wiki

• Informatique :
• Electronique :

Note .

Test fonctionnels

• Sous-système.
  • Sous-système informatique :
  • Sous-système électronique :

Qualité de la réalisation

• Informatique : Note .
  • procédure de test :
  • pages HTML et Javascript :
  • scripts PHP ou programmes C :
  • installation sur FoxBoard :
• Electronique : Note .
  • qualité de la réalisation :
  • tests autonomes :

Bilan

Note finale :

Rapports des élèves

DEMANDE DE RAJOUTER LE PACKAGE MATH POUR FORMULES LATEX S'IL VOUS PLAÎT

Projet SC – Système de contrôle sonar

Pose de la problématique

Voici l'énoncé du sujet :

« Le projet consiste à réaliser un sous-système de contrôle de sonar ultra-sons. L'interface Web associée permettra à l'utilisateur de faire tourner le sonar suivant un angle précis et d'afficher la mesure de distance correspondant à la direction choisie. »

Ainsi, le projet se décompose en deux sous-parties :

• La réalisation informatique

A laquelle Nathan MARTIN et Charlotte BRICOUT furent affectés et qui consiste en la réalisation d’une interface web permettant la gestion des servo-moteurs faisant tourner le sonar selon un angle précis et l’affichage de la distance retournée.

• La réalisation électronique

Sylvain FOSSAERT et Soufiane HADDAOUI s’occuperont quant à eux de la réalisation du sonar proprement dite via la puce FPGA intégré de la NanoBoard et d’un circuit analogique permettant l’adaptation des signaux d’émission et de réception.

Partie Informatique

Partie Electronique

Prise de connaissance du problème

Nous allons dans cette partie, établir notre raisonnement et montrer le résultat obtenu lors de la réalisation du système de mesure de distance via la puce FPGA et d’un circuit d’adaptation de signaux.

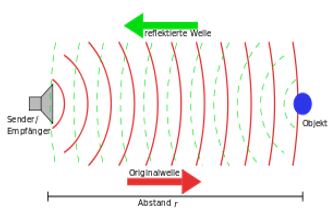
Le module a pour but de mesurer la distance entre la carte et un obstacle. La mesure de distance se base sur la mesure du temps de parcours d'une onde ultrasonore émise puis reçue, après réflexion sur un obstacle.

Ce sous-projet est composé de deux parties :

Une partie implantée dans la carte FPGA de la NanoBoard et une partie analogique réalisée sur une plaque d'essais.

Réalisation de la partie FPGA

La Nanoboard est commandable directement à partir d’un PC contenant le logiciel Altium. Ainsi, en réalisant un montage FPGA sous Altium, celui-ci sera implémenter en VHDL après compilation et il sera alors possible de tester son bon fonctionnement.

Prise en main d’un projet FPGA sous Altium

Afin de comprendre le principe de réalisation sous Altium, nous suivîmes en premier lieu la réalisation effectuée dans l’aide donnée sous forme de PDF. Celle-ci nous a aidé sur la démarche à effectuer mais celle-ci nous a également permis de découvrir des « blocs » que nous pourrons réutiliser par la suite tel que les compteurs par exemple.

Une fois cette initiation réalisée et testée, nous avons commencé à discuter des solutions envisageables afin de répondre au cahier des charges : « La partie implantée dans le FPGA a pour fonction de générer un signal carré à la fréquence de résonance de l'émetteur d'ultrason afin de permettre l'émission du signal. Le début d'émission fera démarrer un compteur (12 bits), qui sera arrêté lors de la réception du signal ultrason sur le récepteur. Ainsi la valeur du compteur correspond à une représentation de la distance parcourue par l’onde ultrasonore. L’écriture de la valeur du compteur en mémoire sera permise grâce à un bit de permission d’écriture. »

Création de la partie émission

Création de l’horloge de résonance

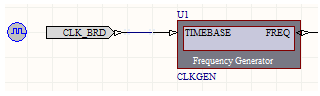
Nous allons créer à partir de la puce FPGA une horloge de 40 kHz correspondant à la fréquence de résonance de notre émetteur ultrasons.

Cette horloge, permettra entre autres d'incrémenter le compteur 12 bits donnant une notion du temps entre l’émission et la réception du signal.

Ainsi, le temps de parcours sera donné par la formule suivante :

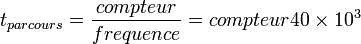
avec :

• Compteur : La valeur décimale du compteur à un instant donné.
• Fréquence : Fréquence d'horloge synchronisée sur la fréquence de résonance du FPGA.

Création du signal d’émission

Cependant, il faut pouvoir envoyer uniquement 10 périodes d’émission à la fréquence de 40 kHz en sortie de la Nanoboard afin de simuler une « slave » d’émission.

Ainsi, nous allons comparer la valeur du compteur 12 bits avec les valeurs 0 et 10 ; lorsque le compteur sera compris entre 0 et 10 un signal logique passera à 1. Ainsi, l’émission sera possible. Si le compteur est supérieur à 10, le signal sera à 0, l’émission sera impossible.

Pour résumer :

• Signal à 1 lorsque 0 ≤ compteur ≤ 10.
• Signal à 0 sinon.

Le compteur est remis à 0 lorsque l'intégralité de la slave est reçue par le récepteur.

La comparaison de ce signal logique avec la fréquence d’horloge permettra d'émettre ou non, d’où l’utilisation des deux portes AND, la première permettant la création du signal proprement dite, la deuxième permettant l’émission du signal à la fréquence de l’horloge (qui est aussi la fréquence de résonance) vers l’émetteur lorsque ce signal est à 1.

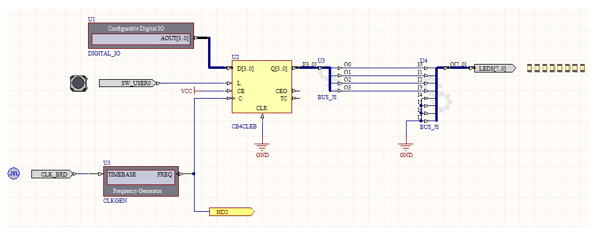
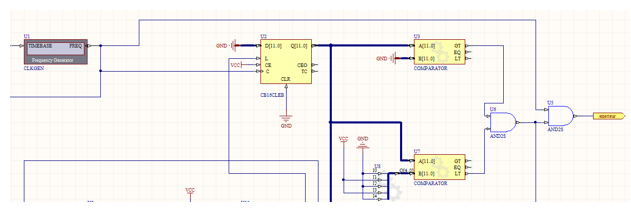
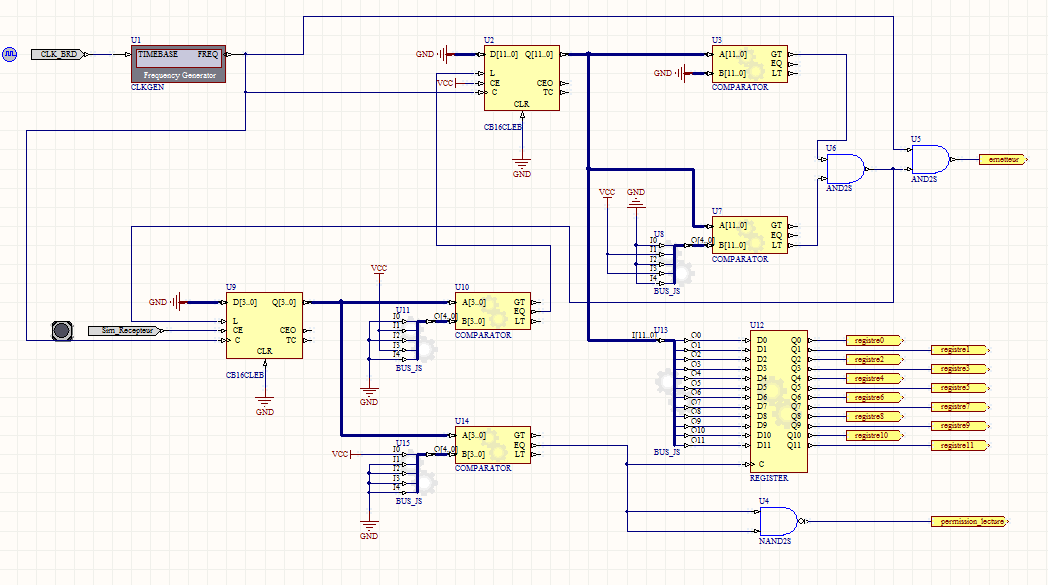
On utilise alors pour réaliser ce système deux comparateurs et deux portes « AND » :

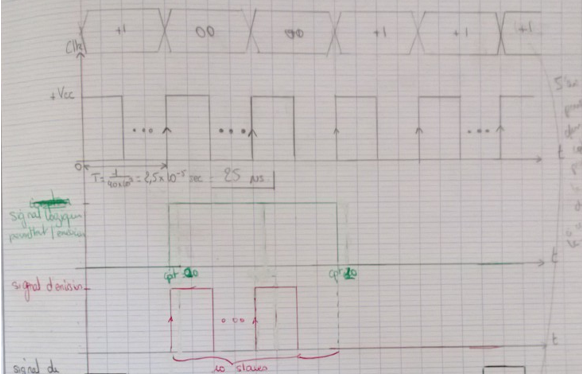
La partie émission est ainsi réalisée. On peut résumer les actions de ce circuit grâce au chronogramme suivant :

Création de la partie réception

Comme dit précédemment, la partie émission attend que l’ensemble des 10 périodes émises soient reçues pour charger la valeur du registre représentant le temps parcouru par le signal pour faire un aller-retour avant de remettre le compteur à 0. Comme demandé dans le cahier des charges, un bit de lecture est mis en place afin que le registre puisse être lu lorsque celui-ci ne change pas d’état, c’est-à-dire qu’il ne doit pas être lu quand une nouvelle valeur est en train d’être écrite dans celui-ci.

Ainsi, le bit de lecture est à 0 pendant l’écriture dans le registre et à 1 sinon. Enfin, il nous faut préciser que le registre change d’état pour prendre la valeur du compteur lors de la première période de réception, et le compteur revient à 0 lorsque la dernière période de réception, la 10Modèle:Exp, est reçue.

Ainsi, on utilise deux comparateurs, l’un pour permettre l’écriture du registre lorsque l’on reçoit la première impulsion de réception, l’autre pour remettre le compteur à 0 lors de la 10Modèle:Exp réception.

Nous avons donc le schéma global suivant répondant à l’ensemble du cahier des charges partie FPGA :

Critique du système réalisé

Distance de détection limitée

Nous allons désormais regarder les limites du système que nous avons réalisé:

On estime que la vitesse du son dans l’air à une température de 25°C est de 346 m.sModèle:Exp.

Le temps maximum effectué par le son pour effectuer un aller-retour (de l’émetteur/objet/récepteur) devra donc être inférieur à la valeur ci-dessous afin d’être pris en compte pour le système mis en place :

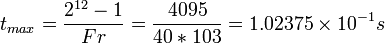
On pourra donc détecter une distance maximale égale à :

Échec d'analyse (fonction inconnue « \itmes »): v=\dfrac{2\times d}{t} \Rightarrow d=\dfrac{v\itmes t}{2}

En prenant Échec d'analyse (fonction inconnue « \maths »): t=t_{max}>\maths> et <math>v=346 m.s^{-1}</maths>, on obtient: <math>d=\dfrac{346\times 0.102375}{2}=17.7 m

La distance maximale détectable par le système que nous allons réaliser sera donc de 17,7 mètres, ce qui cependant, ne semble pas possible vu le matériel que nous allons utiliser.

Remarque : Si on avait voulu détecter un objet à une distance plus importante, il aurait fallu réduire la fréquence d’incrémentation du compteur au détriment toutefois de la précision de la mesure.

Cas de mauvaise réception

Conformément aux explications que notre tuteur nous a octroyées, si l’on ne reçoit pas l’ensemble des périodes de réception, le compteur ne se remettra pas à 0. La saisie de la prochaine réception sera donc faussée. Nous allons donc vous proposer ci-après un nouveau schéma supprimant cette contrainte.

Amélioration du système

Afin de bien tenir compte des nouvelles remarques, et donc d'améliorer la stabilité du système, on modifie le circuit de réception puisque c’est bien lui qui pose problème.

Ainsi, désormais, lorsque qu’un signal est reçu, une bascule D passe à 1, le registre prend donc la valeur du compteur et le bit de permission passe à 0 interdisant ainsi la lecture du registre pendant son changement d’état. Enfin, précisons que le compteur se remet désormais à 0 de lui-même lorsqu’il arrive à 1023.

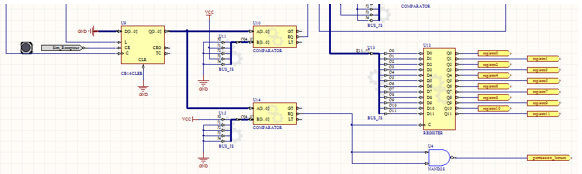
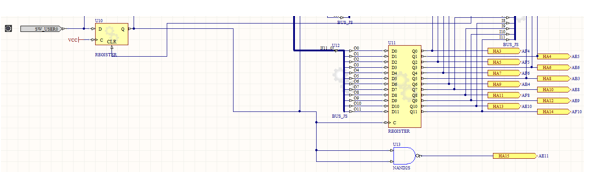
On a ainsi la partie de réception suivante :

Le schéma global devient donc :

Réalisation de la partie analogique

Nous allons désormais répondre à la deuxième partie du projet d’électronique, c’est-à-dire adapter le signal de sortie du FPGA pour qu’il soit compatible avec l’alimentation nécessaire à l’émetteur ultrasons.

Ensuite, nous créerons un circuit permettant d’amplifier le signal reçu par le récepteur afin qu’il soit correctement traité par la puce FPGA.

Adaptation du signal de transmission

L’émetteur doit être alimenté par une tension alternative de fréquence nominale 40 kHz. Nous choisissons donc ici de l’alimenter par une tension alternative de ± 5V. Le signal de sortie du FPGA étant déjà une tension rectangulaire de 0-5V, il nous suffit de créer un montage donnant une tension de sortie de +5V lorsque le signal est à l’état haut et une tension de -5V lorsque le signal du FPGA est à 0V.

D’où le tableau résumé suivant :

Tableau

Tension signal en sortie du FPGA	Tension aux bornes de l’émetteur
0V	-5V
+5V	+5V

Nous allons donc encore une fois réaliser ce montage à l’aide de portes « NAND » de la manière suivante :

Remarque : Les portes « Nand » sont placées en parallèles afin de doubler la puissance disponible aux bornes de l’émetteur. La capacité « Cap » de 10 nF permet d’éliminer la composante continue du signal de sortie.

Idée d’amélioration : Pour que l’émetteur fonctionnement à puissance maximum, on peut créer une tension sinusoïdale à ses bornes en effectuant un filtre passe-bande afin d’extraire l’harmonique de rang 1 du signal rectangulaire (Fourier). Ce filtre peut être créé à partir d’un circuit RLC ou de la manière suivante :

avec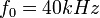

Adaptation du signal de réception

La perte d'amplitude de notre signal est due à la distance que ce dernier a parcourue.

Plus la distance est grande, plus l'amplitude est faible. Il va donc falloir amplifier le signal reçu. Pour réaliser cette amplification, on utilise un montage à AOP (amplificateur opérationnel).

De plus, il est probable que le signal sera parasité, il faut donc dans un deuxième temps le filtrer.

Amplification du signal reçu=

On utilise pour ce faire un AOP en régime linéaire :

On a donc les relations suivantes :

(AOP considéré comme idéal et en régime linéaire)

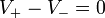
Ici :

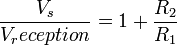
Afin d’avoir un gain de 100, on prend comme valeur R1 = 200 &Omega et R2 = 20 k &Omega. Un tel gain n’est peut-être pas obtenable avec un seule AOP, dans ce cas, il suffit de placer deux AOPs en cascade afin d’obtenir le gain espéré.

Filtrage du signal reçu

Le signal sera filtré de la même manière que le filtrage réalisé sur l’émission, on réalise ainsi le circuit de filtrage suivant :

Échec d'analyse (erreur de syntaxe): G=G_1+G_2 = 20\log\right(\dfrac{1}{\sqrt{1+(R_1\times C_1\times\Omega}^{2}}\left) = 20\log\right(\dfrac{1}{\sqrt{1+\right(\dfrac{1}{R_1\times C_1\times\Omega}\left)^{2}}\left)

Il faut alors déterminer 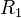, , 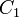, 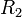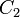afin d’avoir une bande passante de gain maximum à la fréquence .

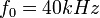Enfin, on vient placer un comparateur à seuil à la sortie du filtre, ainsi lors de le signal dépassera une certaine valeur, la sortie du comparateur passera à 1 signifiant qu’une réception a eu lieu.

Pour aller plus loin=

La solution précédente n’est en réalité pas applicable vu le cout qu’elle représenterait à fabriquer.

Nous allons donc vous proposer une solution entièrement analogique qui ne nécessite pas l’intervention d’une puce FPGA.

Cette partie fut en partie réalisée, mais cependant, de part des problèmes survenus lors de son élaboration, l’intégralité ne fut réalisée.

Simulation de la Nanobord et partie émission

Afin d’établir une fréquence de 40 kHz, qui est normalement donné en sortie de la Nanobord, on utilise un circuit analogique.

Ainsi, à l’aide de deux portes « Nand », on va reproduire un oscillateur de 40 kHz et de rapport cyclique de 0.5. On réalise alors le schéma suivant :

Le FPGA (Nanoboard) prenant le relais par la suite, cette partie est alors terminée.

Dont la fréquence est définie par :

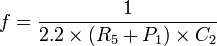
Ainsi, si l’on veut obtenir une fréquence de 40 kHz, on doit trouver les valeurs des composants de valeurs ci-dessous.

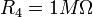
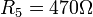
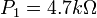
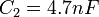
On est alors censé obtenir un oscillateur de rapport cyclique constant égal à 0.5 et de fréquence 40 kHz. Cependant lors de sa réalisation, seul du bruit est visible en sortie (nous sommes donc bloqué ici dans la réalisation).

Aussi, nous souhaitons émettre des « slaves » d’émission de 10 périodes toutes les 25,5 ms. Nous allons donc réaliser ce principe grâce à un circuit permettant de réaliser une horloge de fréquence et rapport cyclique variable : un NE555.

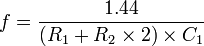
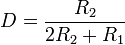
Ainsi, à l’aide des deux équations données dans la documentation constructeur et pour un rapport cyclique de 0.99 et une fréquence de 38 Hz, on obtient les valeurs des composants suivantes :

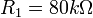
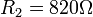
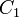prenant pour valeur par défaut 470 nF.

Ces valeurs de composant n’étant pas forcement normalisées ou disponibles, on place sur le circuit les valeurs suivantes :

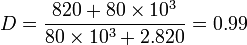
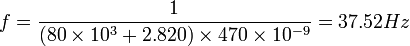
Les oscillogrammes capturés confirment le résultat attendu :

Afin de pouvoir générer 10 périodes à 40 kHz, on inverse le signal en sortie du NE555 (à l’aide d’une NAND), on obtient donc :

Ainsi, en établissant un ET logique entre cette tension et celle de l’oscillateur à 40 kHz, on permet l’envoie d’une slave (10 périodes à 40 kHz) à l’émetteur.

Nous sommes alors censés obtenir la tension désirée représentant la tension de sortie de la Nanobord qui est ensuite envoyé au montage permettant la création d’un signal alternatif de ±5V.

Partie réception

La partie réception quant à elle ne change pas par rapport à la solution impliquant la puce FPGA, c’est-à-dire que l’on effectue une amplification puis un filtre sur le signal reçu.

Conclusion