Commande d'une suspension magnétique : Différence entre versions

Version du 20 mai 2016 à 08:46

Cahier des charges

Présentation générale du projet

Contexte

Un domaine d'application de la mécatronique est celui de la sustentation magnétique par attraction. Cette technique est actuellement abordable autant d'un point de vue technologique qu'économique. Mais pour être efficace, la sustentation magnétique par attraction doit être stable. La suspension magnétique est une technologie avec laquelle l’objet est suspendu par la force électromagnétique. Elle est utilisée dans plusieurs domaines par exemple un système de train magnétique (à Shanghai, Chine).

Objectif du projet

Le but de notre projet est de consister à chercher différentes méthodes pour contrôler et stabiliser un système de suspension magnétique, un système de 3ème ordre.
Après avoir discuté avec notre tuteur,nous devons réaliser le fonctionnement principaux comme ce que ils ont fait à 2013. Nous allons progresser le système si les fonctionnement principaux sont bien realisés.

Description du projet

En effet, contrairement à la lévitation par d'autres moyens, la sustentation magnétique par attraction est instable.Donc, nous devons trouver une méthodes pour contrôler et stabiliser un système de suspension magnétique. lorsque la bille est déplacée vers l'électroaimant, la force magnétique augmente et finit par la faire coller à la buttée haute. A l'inverse, lorsqu'on l'éloigne de l'électroaimant, la force diminue et elle finit par tomber. Le problème est alors de maîtriser la force d'attraction de cet électroaimant et de positionner la boule à une hauteur déterminée avec une dynamique fixée par un cahier des charges.
Ce projet débute par une étude bibliographique sur la modélisation de la suspension magnétique, ainsi que sur différentes techniques de commande de systèmes linéaires. La seconde phase consiste en la prise en main de la plate-forme de contrôle basée sur les logiciels. Ce projet s'achève par la mise en œuvre de quelques méthodes de commande analogiques et numériques ( PID RST et retour d'état principalement) suivie d’une étude comparative de leurs performances.

Choix techniques : matériel et logiciel

* les logiciels: Simulink, Real Time Windows Target.
* le machine:    la suspension magnetique didastel

Problématique

Fonction Transfert pour le système

Simulation sous le logiciel Matlab

Manipulation sur la machine Didastel

Avancement du Projet

Semaine 1(01.25-01.31)

Discussion du sujet, recherches documentaires sur internet, détermines les éléments électroniques à utiliser.

Faire connaissance avec la machine suspension magnétique Didastel et apprendre son fonctionnement.

Après avoir connu les matériaux, nous analysons le système générale. Notre but est de contrôler une Suspension Magnétique, un système non linéaire et instable.

Semaine 2(02.01-02.07)

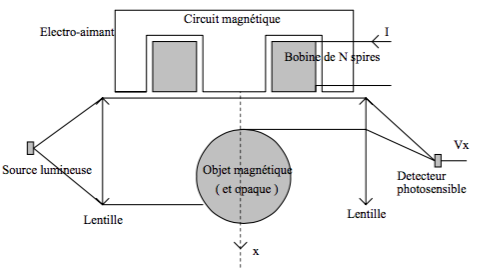
Un objet magnétique est soumis à l'attraction d'un électroaimant dans lequel on contrôle l'intensité, I. Un capteur de position optique permet de mesurer la distance séparant l'objet de électroaimant. Ainsi on peut agir sur la distance mesurée, x, entre cet objet et électroaimant via le courant I, la force d'attraction étant une fonction croissante de l'intensité. La commande du système consiste à contrôler l'intensité, I, en fonction de la distance x.

La distance séparant l'objet de électroaimant est notée x et l'axe x est dirigé positivement " vers le bas "
Le capteur de position associé à son électronique fourni le signal Vx=-a.x ( Vx diminue si x augmente ) donc Vx augmente si x diminue c'est à dire si l'objet monte. Vx représente donc l'altitude de l'objet.
La bobine de électroaimant possède la résistance R et l'inductance L. On négligera l'influence de la position de l'objet ( donc de x ) sur la valeur L.
La masse de l'objet suspendu est M.
L'accélération de la pesanteur est g.
Le courant dans la bobine est I.
La force d'attraction créée par le courant I sur l'objet est F=F(I,x).
La force d'attraction dans la direction x est donnée par la relation : F = − dW où W dx est l'énergie emmagasinée par le système soit:W=1／2＊L* I^2 si le matériau magnétique n'est pas saturé.
Soit:F=1/2*I^2*(−dL/dx)

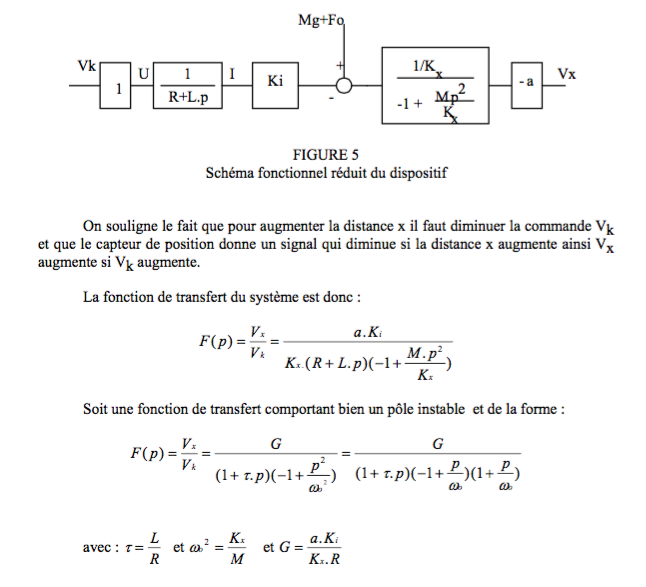
Le contrôle de l'altitude de l'objet s'effectue en contrôlant la force d'attraction c'est à dire le courant, pour ce faire nous modifions la tension (Vk) sur la bobine de électroaimant. Il apparaît donc plus judicieux de régler directement le courant dans la bobine, ainsi la commande sera plus aisée en asservissant le courant plutôt qu'en agissant sur la tension d'alimentation de électroaimant. Nous allons donc étudier le cas où le courant est asservi.
Nous utiliserons donc toujours une commande en courant de électroaimant plutôt qu'une commande en tension car ainsi le modèle est seulement du second ordre au lieu du troisième ce qui conduira à une commande plus aisée et à des performances dynamiques meilleures.

Semaine 3(02.08-02.12)

A L'aide du document"Mise en Equation de la suspension magnétique.pdf", nous avons bien compris ce système, Ce système est divisé en 3 parties. Pour la partie électro-aimant, on injecte d'abord une tension qui va surement créer un courant électrique, le champ magnétique ainsi créé provoque une force qui soutient le ballon dans la position désirée.

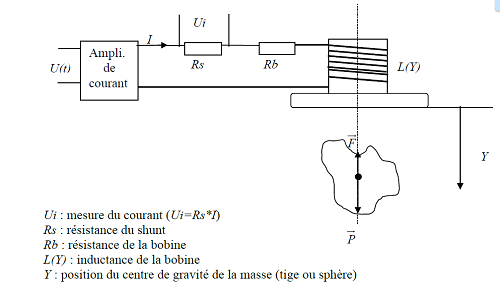
selon cette image,La masse est soumise à deux forces opposées :

F force d'attraction de l'électroaimant

P force d'attraction terrestre qui a pour module: P=mg.
La force F est engendrée par le courant I qui parcours la bobine et dépend aussi de Y.l'équation du mouvement est donnée par la loi fondamentale de dynamique: md2Y/dt2 = mg - F(Y,I).
le courant I est fourni par un amplificateur de courant à partie de la tension de commande U(t). cette boucle de courant peut être modélisée par un circuit RL, donc l'équation électrique: kU = RI + L dI/dt.
ce système est donc régi par les deux équation suivant:

md2Y/dt2 = mg - F(Y,I)

kU = RI + L dI/dt
les fonctions de transfert de ce système :

partie électrique:
G_1=(I(p))/(U(p))=K_1/(1+τ_e∙p)

partie mécanique:
G_2=(X(p))/(I(p))=K_2/(1-〖τ_m〗^2∙p^2 )

la fonction de transfert globale:
G=(-K)/((1+τ_e∙p)∙(1-〖τ_m〗^2∙p^2))

Semaine 4(02.22-02.28)

Après avoir étudié notre système, nous commençons à simuler la partie électronique et la partie mécanique sous matlab.
Nous étudions le système en boucle ouvert et remarquons la réponse ‘step’ et le schéma nyquist, selon le schéma et la théorie, le système n’est pas stable. Quand nous avons une entrée de la fonction ‘step’, nous avons obtenu ces résultats.(la réponse, le schéma nyqusit, le schéma bode)

Notre tuteur alors nous conseille que utiliser la correcteur PID pour stabiliser le système. Nous commençons à chercher les valeur de la correcteur PID.

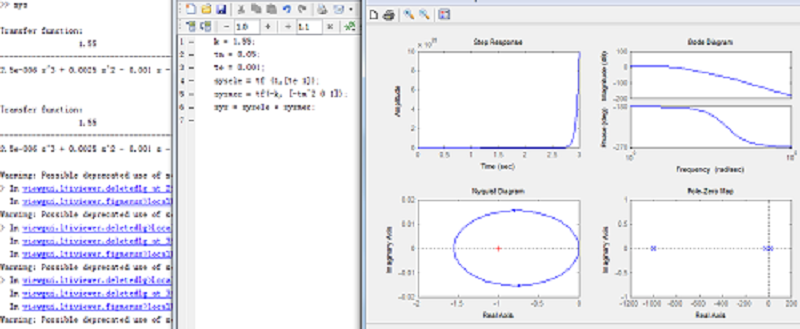
Semaine 5(02.29-03.06)

Cette semaine, nous avons essayé de utiliser la correcteur PID pour stabiliser notre système. Il faut déterminer les paramètres, nous avons cherché les informations sur Internet, nous avons plusieurs méthodes pour déterminer ces paramètres.

    
%opts = pidtuneOptions('CrossoverFrequency',32,'PhaseMargin',90);  
    
%[C, info] = pidtune(T, 'pid', opts)

Grâce aux formules dessus, nous trouvons les valeur kp et wi. Selon la théorie, nous calculons les valeurs de kp, ki, kd qui sont presque parfait:

%kp = 0.6471;

%ki = 2.949;

%kd = 0.737; Avec ces valeurs, nous pouvons obtenir la réponse suivante:

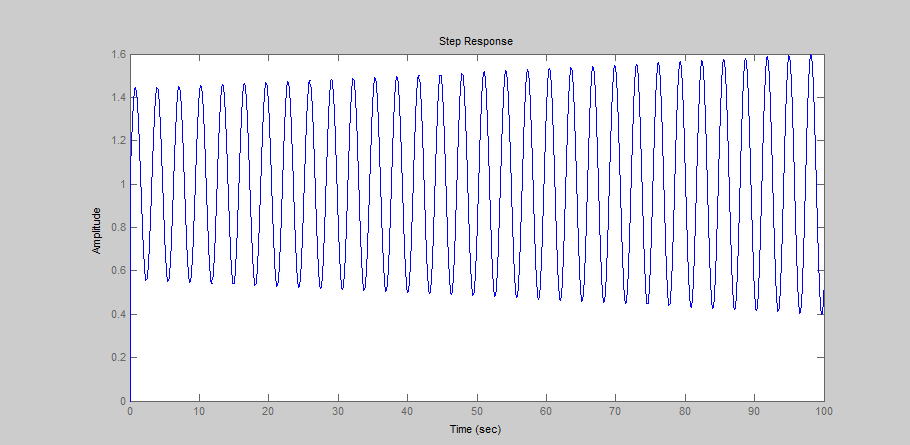
Nous voyons que le système est presque stable, mais pas très précis. Après la modification, nous avons ces valeur finales kp = 30, ki = 50, kd = 6.
la réponse de la fonction de step:

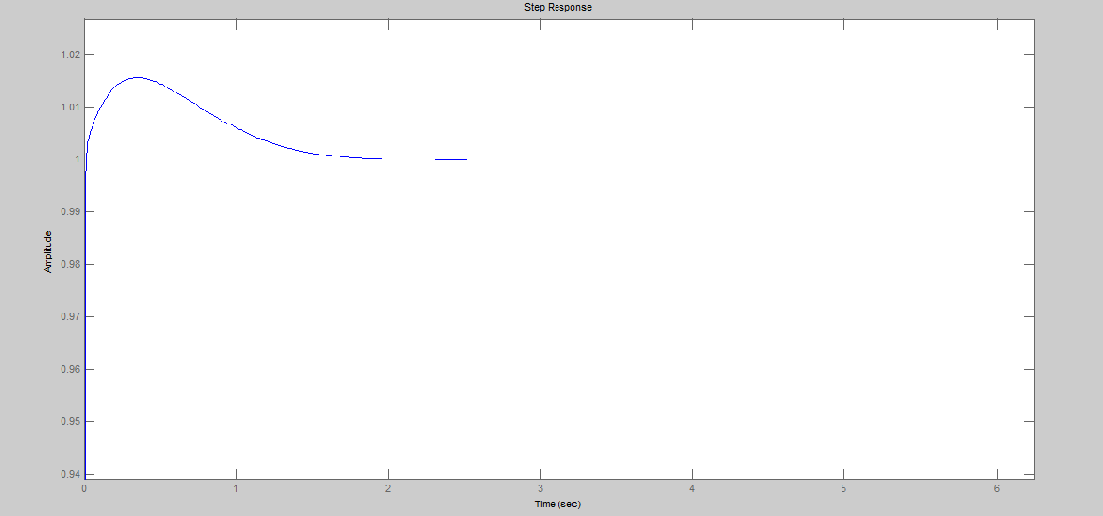
Nous avons obtenu le système stable et plus précis.

Semaine 6(03.07-03.13)

Cette semaine, nous avons essayé d'utiliser le simulink avec les paramètres que nous avons trouvé, mais nous n’avons pas arrivé au bon résultat, notre système est encore instable. Car nous nous sommes trompé le pidtune et le pid. Donc, le professeur nous conseille d'utiliser l’autre méthode (retour d’état) pour stabiliser notre système.

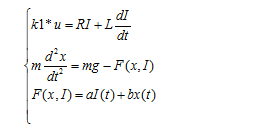
Avec k1 = 0.24, te = L/R = 0.001s
On néglige la gravité mg:
Avec tm = m/b, k2 = -a/b=-25.8, tm = 0.05
On pose:

X1: la position de ballon

X2: la vitesse de ballon

X3：la courant

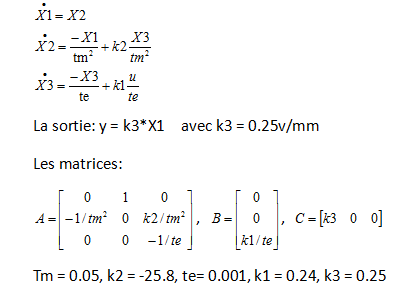
Semaine 7(03.14-03.20)

On peut trouver les poles du sys p1 = -1/te, p2 = -1/tm, p3 = 1/tm;
Comme p3 est positive, donc le système est instable, on doit déplacer les pôles p2 et p3.
On pose:
Z= 0.707, wn = 35
On utilise le matlab pour trouver les deux pole, p2 = -24.7450+24.7525i P3 = -24.7450-24.7525i.

Et utilise ce schéma pour tester

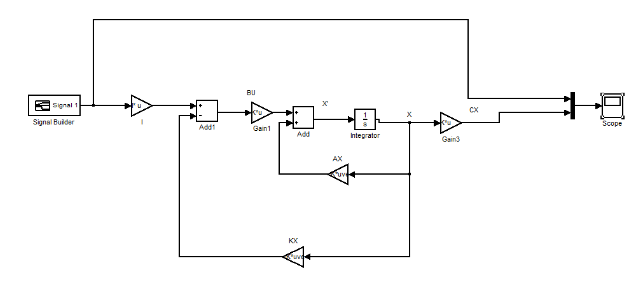
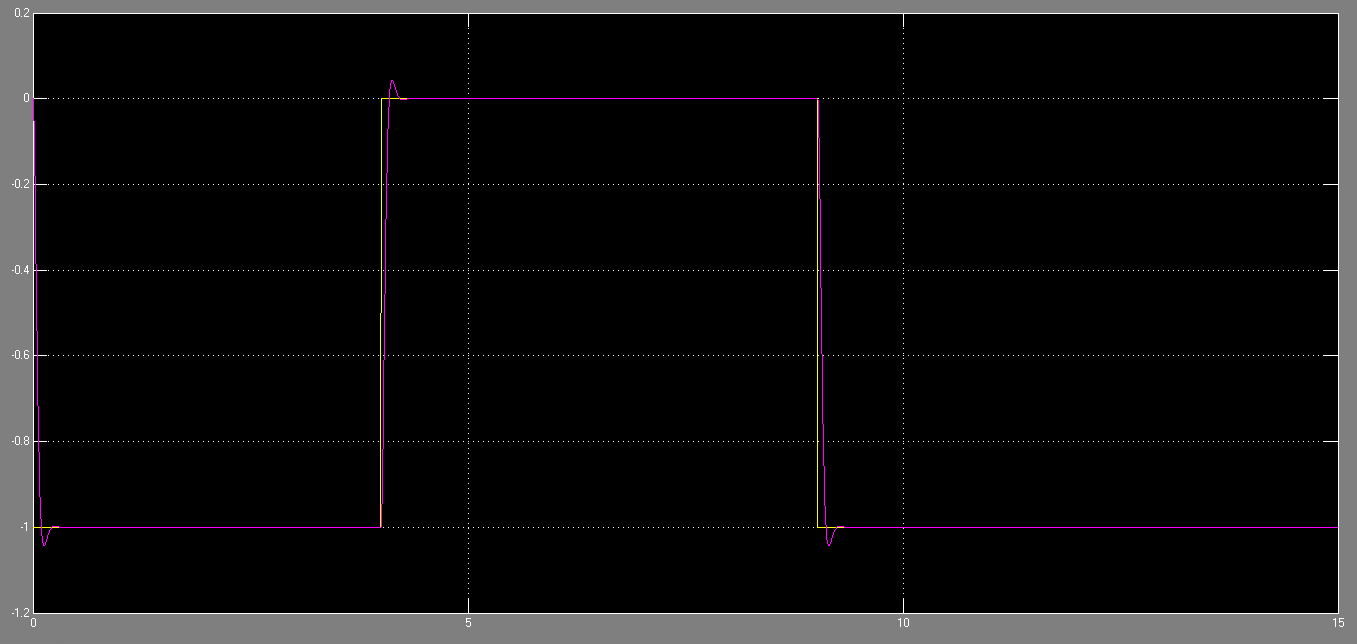
On peut trouver que notre système est bien stable et correspondant, mais il y a aussi un peu de dépassement.

Semaine 8(03.21-03.27)

On attaque l'obeservateur du systeme cette semaine.
Un conservateur est pour le but deobserver les états du système que nous pouvons pas les mesurer directement dans le système.
Par exemple, la variation du courant de la machine et de la vitesse du ballon ne peuvent pas être mesuré. C’est la raison pour laquelle nous avons besoin d’un observateur.

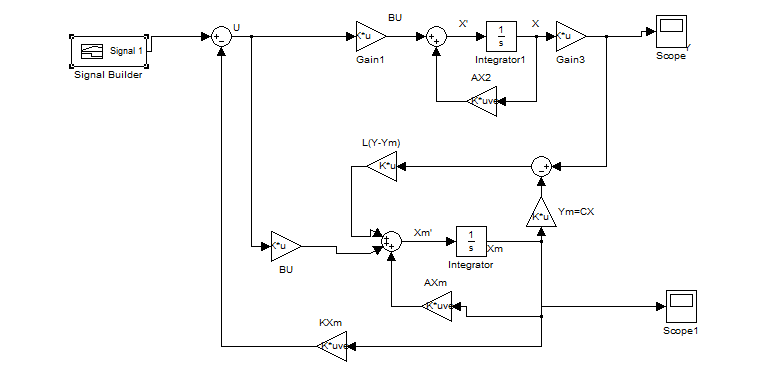
L’observateur dans notre schéma bloc est effectivement une copine du système réel. Cependant, les variable sont pas les valeurs en temps réel. Il faut donc bien choisir les paramètres de la matrice L pour que les erreurs entre les valeur estimés et les valeurs réels soient plus petites.
Et voici ce que nous avons observé sur la variation du courant, de la vitesse et de la position

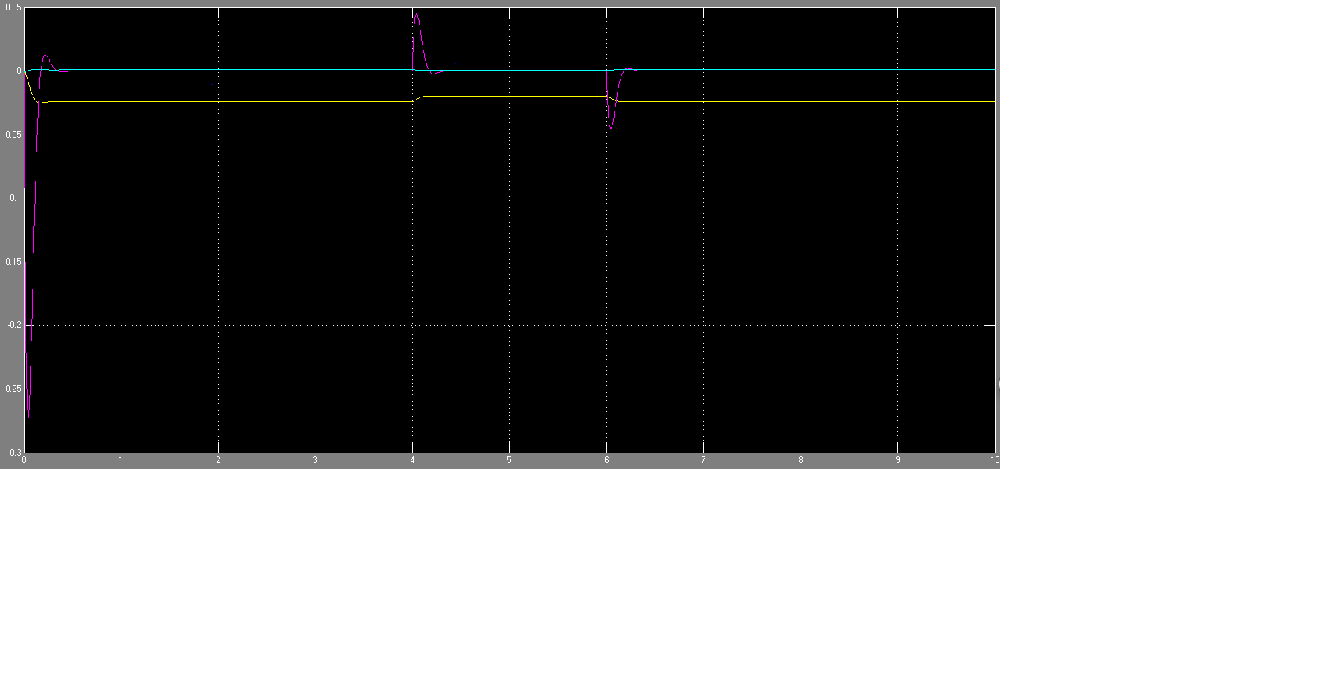
Semaine 9(03.28-04.03)

Nous essayons une méthode avancement du phase pour ce système.
En considérant un système dont la fonction de transfert en boucle ouverte est H(jw). En boucle fermée, il aura une fonction de transfert : H(jw)/(1+H(jw))
Comme notre système est 3ème ordre, et instable.
Nous pouvons obtenir le Bode diagram suivant:

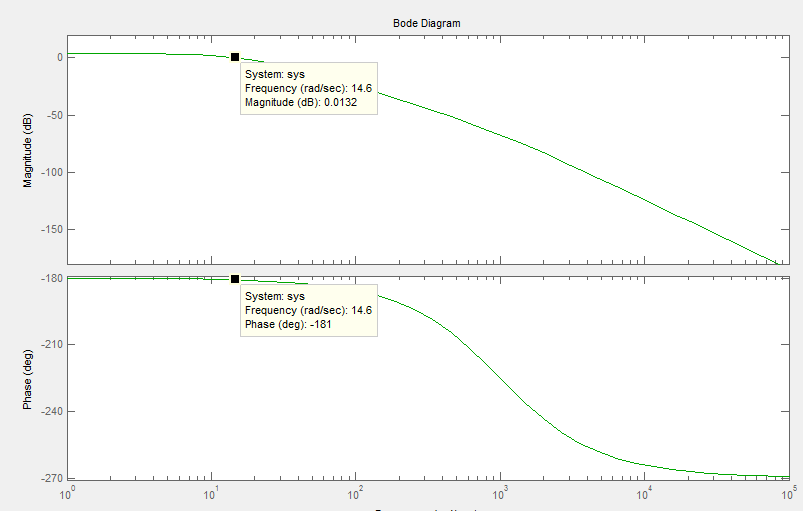
Quand magnitude(db) = 0db, et le phase > -180, le système est stable. Cependant, pour notre système, quand le magnitude = 0db, le phase < 180, donc , notre système est instable.
Donc, nous utilisons la méthode avance de phase afin de stabiliser notre système. Nous désirons apporter un déphasage de 30°, alors -181°+30° = -151° > -180°. Notre système deviendras stable.

Nous pouvons utiliser ces formules pour calculer a, et en plus Wc = 1/(ta). Nous pouvons alors avoir le t.
Quand les valeurs de t et a sont terminés, le correcteur avance phase est fixé.
Nous les appliquent sur matlab.
Nous avons alors un nouveau Bode diagram:

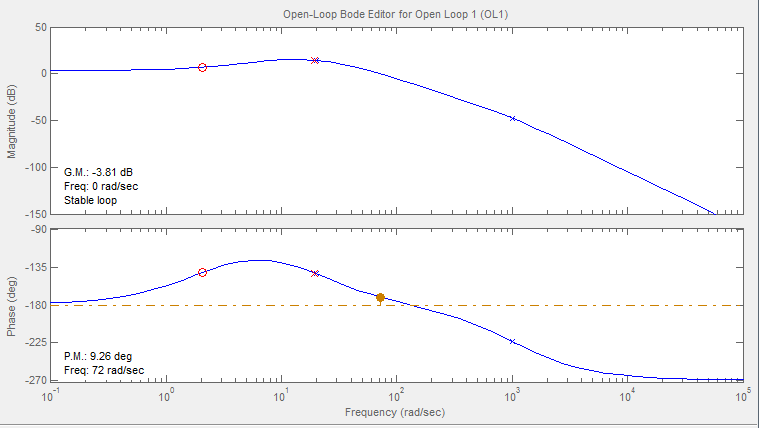
notre système est maintenant stable grâce à .

Semaine 10(04.18-04.24)

Le prof nous a posé la question sur les équations qui définissent le système de la suspension magnifique.
Donc cette semaine nous avons utilisé deux méthodes différents a fin de vérifier le système.
le but est de vérifier si nous pouvons définir le même système avec deux méthodes différents.

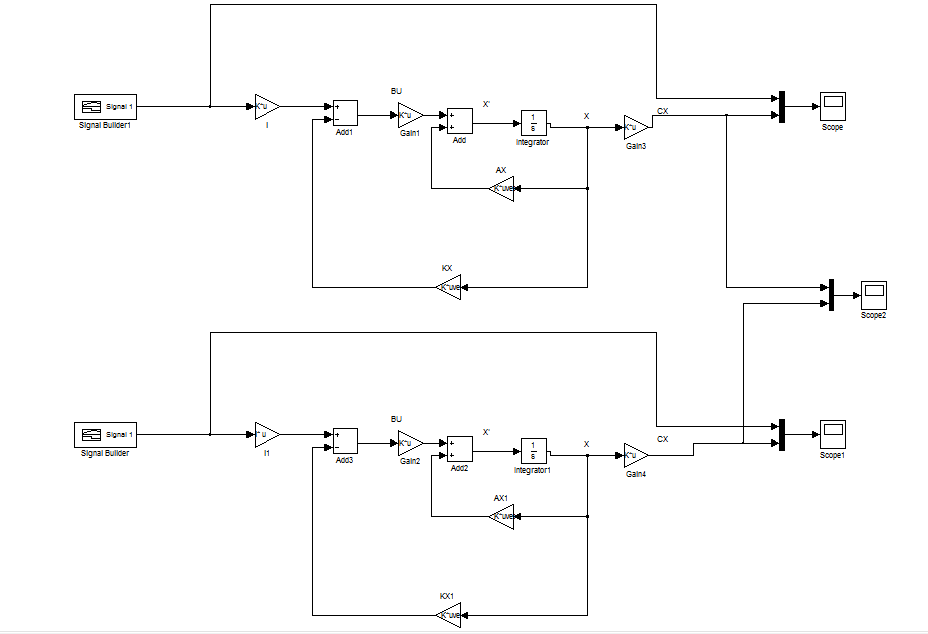
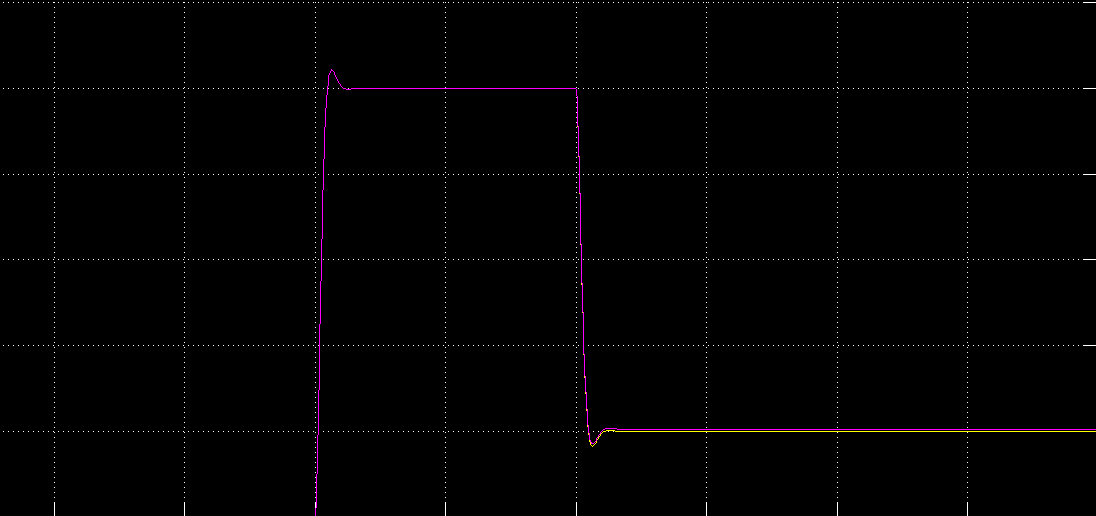
on remarque bien que les deux méthodes définissent le même système.

Semaine 11(04.24-04.30)

Nous attaquons alors la partie manipulation de notre machine.
C'est la partie plus important mais aussi plus difficile.
Dans la partie de la simulation, nous avons toujours un bon résultat, puis que nous simulons dans un système bien linéaire.
Nous avons rencontré des gros soucis au début puisque nous avons essayé plusieurs façons à simuler le système réel (les équations d'état) sous matlab.
Il sont tous une approximation du système réel mais certain méthode n'est pas assez précis à cause de certains négligences ou approximation de notre calculation.

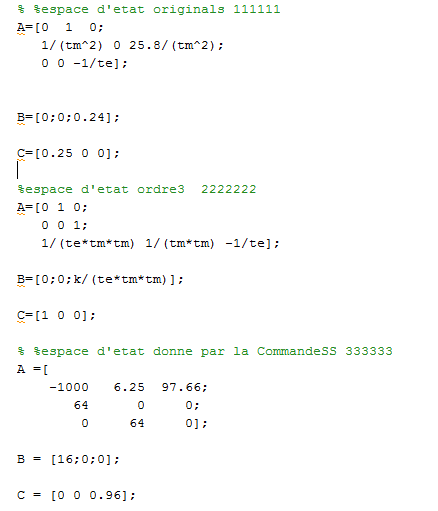
Nous finalement fixons à la méthode de troisième ordre avec les équations calculé par la fonction transfert après avoir exécuté plusieurs essais.

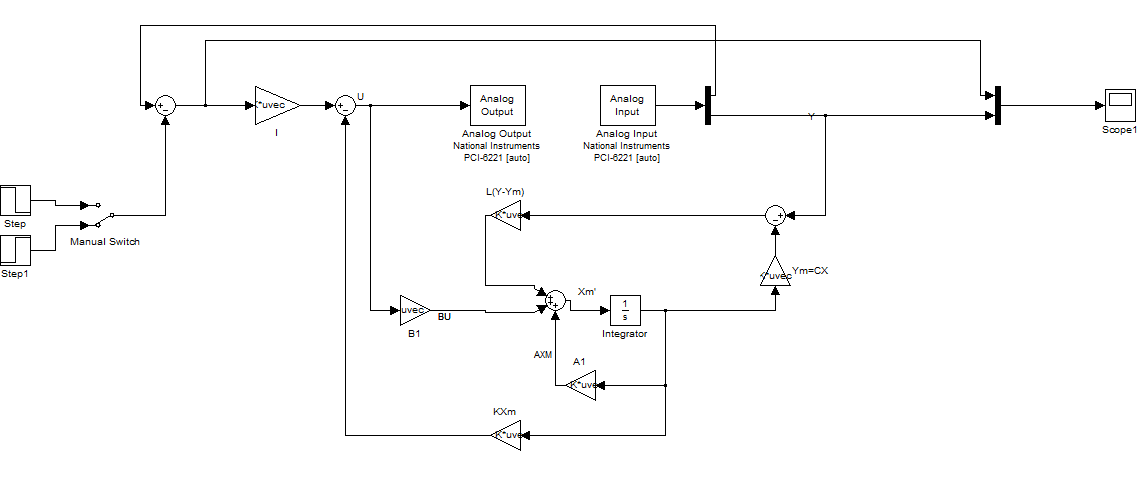
En jouent sur le temps d'échantillonnage, l'amortissement, les pôles de l'observateurs, nous avons à la fin réussi à stabiliser notre système.

rapport

Fichier:Rapport.pdf

@@ Ligne 174 : / Ligne 174 : @@
 <br>En jouent sur le temps d'échantillonnage, l'amortissement, les pôles de l'observateurs, nous avons à la fin réussi à stabiliser notre système.
 <br>[[Fichier:suspension finale.png]]
+===rapport===
+[[Fichier:rapport.pdf]]