IMA5 2018/2019 P18 : Différence entre versions
(→Semaine 5) |
(→Simulation) |
||
| (137 révisions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 160 : | Ligne 160 : | ||
la modulation AM pour la modulation FM, permettant d'obtenir un meilleur signal en réception. | la modulation AM pour la modulation FM, permettant d'obtenir un meilleur signal en réception. | ||
| − | === Antennes | + | === Antennes === |
L'antenne a un rôle très imporant dans les liaisons hertziennes, elle assure l'interface entre le circuit électronique et le milieu de propagation. | L'antenne a un rôle très imporant dans les liaisons hertziennes, elle assure l'interface entre le circuit électronique et le milieu de propagation. | ||
| Ligne 199 : | Ligne 199 : | ||
| + | ===Bilan de liaison=== | ||
Le '''bilan de liaison''' d'une liaison hertzienne permet de déterminer si le niveau de puissance reçu par le récepteur sera suffisant pour que la liaison fonctionne correctement. | Le '''bilan de liaison''' d'une liaison hertzienne permet de déterminer si le niveau de puissance reçu par le récepteur sera suffisant pour que la liaison fonctionne correctement. | ||
En effet si la puissance reçue est trop faible, le dispositif électronique de réception n'a pas la sensibilité nécessaire pour extraire le signal pertinent. | En effet si la puissance reçue est trop faible, le dispositif électronique de réception n'a pas la sensibilité nécessaire pour extraire le signal pertinent. | ||
| Ligne 232 : | Ligne 233 : | ||
==Semaine 1== | ==Semaine 1== | ||
| − | + | Les schémas ci-dessous présentent la structure de notre système radio | |
| − | |||
| − | |||
| − | |||
| − | |||
==== Structure de l'émetteur ==== | ==== Structure de l'émetteur ==== | ||
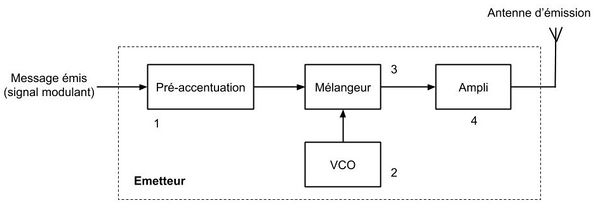
| − | [[Fichier: | + | [[Fichier:Emetteur_schema_fonctionnel.jpg|600px|center]] |
<center>''fig 2. schéma fonctionnel de l'émetteur ''</center> | <center>''fig 2. schéma fonctionnel de l'émetteur ''</center> | ||
| Ligne 271 : | Ligne 268 : | ||
:'''3''' . d'un mélangeur | :'''3''' . d'un mélangeur | ||
| − | Le mélangeur est un composant électronique permettant d'assurer la fonction "changement de fréquence" en réalisant la translation du spectre de ce signal. | + | Le mélangeur est un composant électronique permettant d'assurer la fonction "changement de fréquence" en réalisant la translation du spectre de ce signal. |
| + | Le mélangeur idéal est un multiplieur : il permet de multiplier deux signaux d'entrée pour obtenir en sortie un signal dont les fréquences ont été additionnées ou soustraites. | ||
| + | Quelques formules de trigonométries s'imposent : | ||
| + | |||
| + | Soit, | ||
| + | |||
| + | <math>S_{rf} = A_{rf} cos( \omega_{rf} t + \phi_{rf} ) </math> | ||
| + | |||
| + | et | ||
| + | |||
| + | <math>S_{ol} = A_{ol} cos (\omega_{ol} t) </math> | ||
| + | |||
| + | respectivement le signal modulant et le signal de l'oscillateur local. | ||
| + | |||
| + | Le mélangeur assure une opération de multiplication, on se retrouve donc en sortie avec un signal de la forme : | ||
| + | |||
| + | <math>S_{fi} = K(A_{ol} cos (\omega_{rf} t+ \phi_{rf} ) * A_{rf} cos(\omega_{ol} t)) </math> | ||
| + | |||
| + | Or, | ||
| + | |||
| + | <math> cos(a) \times cos(b)= \frac{1}{2}(cos(a+b)+cos(a-b)) </math> | ||
| + | |||
| + | Donc, | ||
| + | |||
| + | <math>S_{fi} = \frac{K}{2}A_{ol}A_{rf} (cos ((\omega_{rf}+\omega_{ol})t+ \phi_{rf} ) + cos((\omega_{rf}-\omega_{ol})t+ \phi_{rf} )) </math> | ||
| + | |||
| + | |||
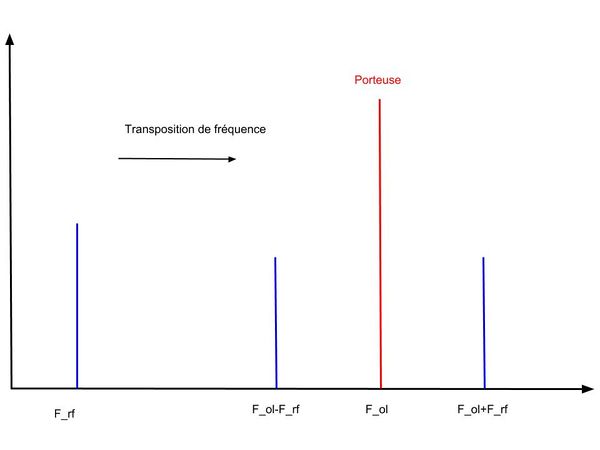
| + | Graphiquement, on retroue les deux composantes <math>\omega_{rf}+\omega_{ol}</math> et <math> \omega_{rf}-\omega_{ol} </math> | ||
| + | de part et d'autre de la porteuse ( l'oscillateur local). | ||
| + | |||
| + | |||
| + | [[Fichier:Transposition frequence spectre.jpg|600px|center]] | ||
| + | <center>''fig 3. transposition de fréquence ''</center> | ||
| + | |||
| + | |||
| + | |||
| + | Il est important de noter que seule l'une des deux raies sera utilisée. On verra en quoi le problème de la '''fréquence image''' peut poser problème dans le cas de la réception. | ||
| + | |||
| Ligne 281 : | Ligne 315 : | ||
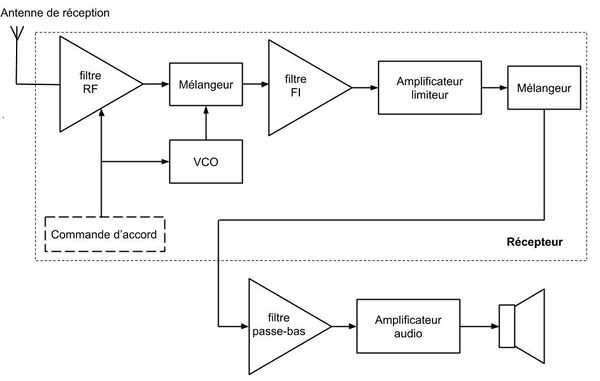
| − | + | [[Fichier:Recepteur_schema_fonctionnel.jpg|600px|center]] | |
| − | + | <center>''fig 4. schéma fonctionnel du récepteur''</center> | |
| − | + | ||
| + | Le synoptique ci-dessus présente le récepteur FM couplé à l'amplificateur audio permettant l'écoute du signal démodulé. | ||
| + | Ce récepteur est composé de : | ||
| + | |||
| + | |||
| + | :'''1''' . d'une '''antenne de réception''' (!). Celle-ci doit encore une fois être dimensionner de telle sorte que le maximum de puissance | ||
| + | soit reçu sur la bande de fréquence désirée. | ||
| + | |||
| + | :'''2''' . d'un '''filtre RF'''. Ce filtre est censé sélectionner la bande de fréquence à démoduler. Il permet de ne présenter au premier mélangeur que la | ||
| + | bande désirée et ainsi d'éviter de démoduler la '''fréquence image'''. | ||
| + | |||
| + | :'''3''' . d'un premier mélangeur qui assure l'abaissement de fréquence vers une fréquence intermédiaire de 10.7Mhz. | ||
| + | |||
| + | :'''4''' . d'une '''commande d'accord''' : celle-ci permet de régler à la fois la sélectivité du filtre RF et la fréquence du VCO. | ||
| + | Les deux fonctions électroniques sont réglés conjointement : le circuit est donc accordé. | ||
| + | |||
| + | :'''5''' d'un '''filtre FI''' qui permet de ne récupérer que la nouvelle fréquence centrale issue de la transposition de fréquence ( Fi = F_rf - F_ol). | ||
| + | Cette fonction est assurée par un filtre céramique. | ||
| + | |||
| + | :'''6''' d'un '''amplificateur limiteur'''. Le détecteur FM est différent du détecteur AM, car il est sensible à la modulation de fréquence et insensible aux variations d’amplitude de la porteuse. | ||
| + | L'information audiofréquence étant inscrite dans la fréquence instantanée , nous pouvons amplifier et écrêter le signal FI , ce qui permettra de supprimer une grande partie des parasites qui se seront ajoutés au signal au cours de la transmission : c'est le rôle de l'amplificateur-limiteur. | ||
| + | |||
| + | :'''7''' d'une autre mélangeur, il s'agit d'un '''démodulateur de fréquence à quadrature'''. | ||
| + | L'idée par rapport à un mélangeur classique est que ce démodulateur ne mélangeur pas deux signaux de fréquence différents mais deux signaux de fréquence identique mais de phase différente. | ||
| + | |||
| + | :'''8''' d'un '''filtre passe-bas'''. Comme nous l'avons indiqué le signal émis a d'abord été pré-accentué. Le filtre passe-bas devra donc prendre en compte cette déformation du signal. | ||
| + | Ainsi, le filtre passe-bas aura sa fréquence de coupure non pas à 15kHz mais à la fréquence de coupure de l'étage de pré-accentuation, c'est-à-dire 3180 Hz. | ||
| + | |||
| + | :'''9''' d'un '''amplificateur audio''' classique, basé autour d'un LM386. | ||
==Semaine 2== | ==Semaine 2== | ||
| − | + | '''Descriptif de l'émetteur radio''' | |
| + | |||
| + | === Topologie de l'émetteur === | ||
| + | |||
| + | |||
| + | [[Fichier:Topologie_emetteur_reelle.jpg|1000px|center]] | ||
| + | <center>''fig 5. Topologie de l'émetteur''</center> | ||
| + | |||
| + | Cet émetteur s'inspire des travaux de Remy Mallard ( émetteur FM 003 https://sonelec-musique.com/ ) | ||
| + | |||
| + | === Alimentation du circuit === | ||
| + | |||
| + | L'alimentation peut être effectuée grâce à un régulateur de tension 12V ( composant assez classique ). | ||
| + | On notera toutefois que deux filtres passe-bas permettent de découpler la section haute fréquence des autres éléments du circuit. | ||
| + | Ainsi, le filtre passe-bas en pi composé de de L0, C5 et C7 permet d'éviter que les signaux hautes fréquences ne viennent perturber l'alimentation. | ||
| + | L'autre filtre passe-bas du second ordre, formé par l'inductance L1 et C8 permet d'alimenter la section BF sans la HF ne vienne perturber | ||
| + | son fonctionnement( parmi les erreurs de simulation commises, nous avons pu remarqué qu'un signal de "moyenne fréquence" non filtré par ce filtre | ||
| + | perturbait l'alimentation de l'ampli op et déformait complètement le signal ). | ||
| + | |||
| + | === Section basse-fréquence === | ||
| + | |||
| + | La première observation notable dans cette section est que l'amplificateur opérationnel choisi est doté d'une alimentation simple alors qu'a priori, | ||
| + | le signal audio d'entrée attaque d'abord un condensateur de liaison : le signal gravite donc autour d'un potentiel de 0 Volt. | ||
| + | Si un tel signal attaquait directement l'entrée de l'ampli op, on peut être certain que le signal serait écrêté. Un ampli op d'alimentation simple ne | ||
| + | peut opérer que sur des signaux dont l'amplitude correspond à son alimentation, et même, on peut s'attendre à une certaine chute de tension d'un ou deux Volts. | ||
| + | Donc dans notre cas, les signaux que peut traiter notre ampli op sans les distordre doivent être compris entre 2 et 10 V. | ||
| + | |||
| + | Le diviseur de tension formé par R1, R2 permet de centrer le signal audio autour d'un potentiel de 6V, ce qui rend possible | ||
| + | l'opérabilité de l'AOP. La diode Zener D1 joue le rôle de régulateur, elle permet de stabiliser la tension à ses bornes à une valeur voulue | ||
| + | en absorbant plus ou moins de courant selon les besoins de la charge, R2 ici. ( voir [http://subaru.univ-lemans.fr/AccesLibre/UM/Pedago/physique/02/electro/zener.html] | ||
| + | pour une explication imagée et intuitive.) | ||
| + | |||
| + | L'amplifaction opérationnel permet d'effectuer l'opération de '''préaccentuation'''. La norme est celle de la préaccentuation 50µs, qui correspond à une fréquence de 3180 Hz. | ||
| + | Le montage de l'amplificateur est celui d'un amplificateur non-inverseur tel que : | ||
| + | |||
| + | <math> \frac{OpV_{out}}{OpV_+} = 1 + \frac{Z_1}{Z_2} </math> | ||
| + | |||
| + | avec | ||
| + | |||
| + | <math> Z_1 = R_5 // Z_{C_2} </math> | ||
| + | |||
| + | <math> Z_2 = R_3 + Z_{C_6} </math> | ||
| + | |||
| + | |||
| + | L'objectif de cet étage est d'amplifier uniquement les fréquences supérieures à 3180 Hz. | ||
| + | Ainsi pour cette fréquence de coupure, le signal doit être amplifié de 3dB. | ||
| + | |||
| + | Une analyse par pôles dominants permet de déterminer la fréquence de coupure voulue. | ||
| + | Le gain doit être unitaire pour les fréquences inférieurs à 3180 Hz. | ||
| + | |||
| + | En supposant pour les basses fréquences, | ||
| + | |||
| + | |||
| + | <math> Z_{C_2} \gg Z_{C_6} \gg R_5 \gg R_3 </math> | ||
| + | |||
| + | on a : | ||
| + | |||
| + | <math> \frac{OpV_{out}}{OpV_+} \sim 1 + \frac{R_5}{Z_{C_6}} \sim 1 </math> | ||
| + | |||
| + | Quand la fréquence augmente, la réactance de C6 diminue de sorte que la relation <math> Z_{C_6} \gg R_5 </math> n'est plus valide. | ||
| + | Ainsi la première fréquence de coupure est atteinte lorsque | ||
| + | |||
| + | <math> f_{c_1} = \frac{1}{2\pi C_6 R_5} = 3180Hz </math> | ||
| + | |||
| + | Le gain est à présent fonction de la fréquence avec une pente de 6dB/octave | ||
| + | |||
| + | <math> \frac{OpV_{out}}{OpV_+} \sim 1 + \frac{R_5}{C_6}\omega </math> | ||
| + | |||
| + | La deuxième contrainte est imposée par la deuxième fréquence de coupure. Elle doit être strictement supérieur à 20kHz ( limite du spectre sonore ) de sorte | ||
| + | que le gain soit toujours augmenté jusqu'à cette limite. | ||
| + | |||
| + | Cette deuxième fréquence de coupure est atteinte lorsque la réactance de C6 croise la résistance de R3. | ||
| + | Dans ce cas. on obtient : | ||
| + | |||
| + | <math> f_{c_2} = \frac{1}{2\pi C_6 R_3} </math> | ||
| + | |||
| + | Le gain vaut alors : | ||
| + | |||
| + | <math> \frac{OpV_{out}}{OpV_+} \sim 1 + \frac{R_5}{R_3} </math> | ||
| + | |||
| + | Avec les valeurs de notre schéma, on obtient donc : | ||
| + | |||
| + | |||
| + | <math> f_{c_1} = \frac{1}{2\pi C_6 R_5} = \frac{1}{2\pi.1.10^{-9}.47.10^3} = 3380 Hz</math> | ||
| + | |||
| + | <math> f_{c_2} = \frac{1}{2\pi C_6 R_3} = \frac{1}{2\pi.1.10^{-9}.3,3.10^3} =48kHz</math> | ||
| + | |||
| + | La valeur du condensateur C2 doit être choisie de façon à ce que la relation <math> Z_{C_2} \gg Z_{C_6} \gg R_5 \gg R_3 </math> reste valable dans le domaine sonore. | ||
| + | |||
| + | La réponse du système pour ces valeurs est donnée par le graphe ci-dessous. | ||
| + | |||
| + | [[Fichier:Reponse_frequentielle_preaccentuation.JPG|1000px|center]] | ||
| + | <center>''fig 6. préaccentuation du signal sonore pour transmission hertzienne''</center> | ||
| + | |||
| + | ===Section haute fréquence === | ||
| + | |||
| + | L'oscillateur que nous utilisons dans cet étage est un VCO LC à transistors couplés en croix ( ''Cross-coupled LC VCO'' ) dont la fréquence de résonance dépend de l'inductance L3 et des condensateurs. | ||
| + | |||
| + | ''' Circuit LC''' | ||
| + | |||
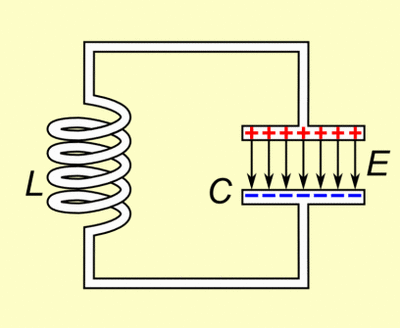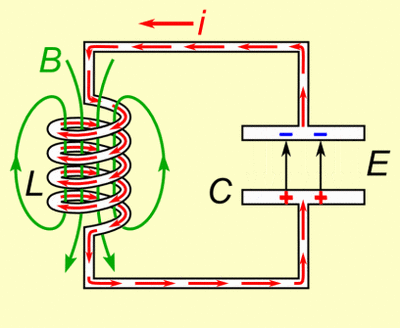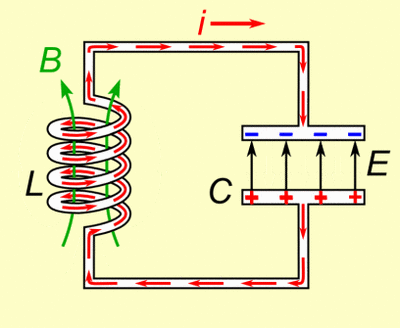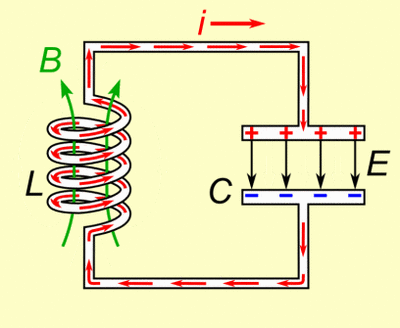
| + | Un circuit LC stocke de l'énergie électrique. Le condensateur stocke de l'énergie dans le champ électrique E entre ses plaques et l'inductance stocke de l'énergie dans son champ magnétique ( qui dépend du courant la traversant.) | ||
| + | |||
| + | Si l'inductance est connectée à un condensateur chargée, le courant commence à traverser la self et celle-ci commence à stocker de l'énergie dans son champ magnétique. Ce faisant, le condensateur commence à se décharger jusqu'à ce que toute la charge soit partie et que la tension à ses bornes atteignent 0. Mais le courant délivré par l'inductance va commencer à charger le condensateur avec un voltage de polarité inverse. | ||
| + | L'énergie requise pour charger le condensateur est donc extraite du champ magnétique Quand le champ magnétique est complètement dissipé, le courant stoppe et la charge est de nouveau stockée dans le condensateur, avec une polarité inverse à celle de la condition initiale. Le cycle se répète et la bobine est de nouveau chargée mais le sens du courant est lui aussi inversé. | ||
| + | |||
| + | la fréquence de résonance d'un circuit LC est donné par : | ||
| + | |||
| + | <math>\omega_0 = \frac{1}{\sqrt{LC}}</math> | ||
| + | |||
| + | Il est à noter que ni les inductances ni les condensateurs ne sont parfaits, si le circuit n'est pas alimenté par un circuit extérieur, les résistances parasites finiront par dissiper toute | ||
| + | l'énergie jusqu'à ce que les oscillations cessent. | ||
| + | |||
| + | [[Fichier:Tuned_circuit_animation_3_300ms.gif|400px|center]] | ||
| + | <center>''fig 7. Charge et décharge du condensateur et de l'inductance dans un circuit LC parallèle''</center> | ||
| + | |||
| + | |||
| + | Dans notre cas, l'inductance de la résonance est L3 ( ou L4 et L5, ce qui revient au même). | ||
| + | De nombreux éléments capacitifs jouent un rôle dans la résonance. Il y a les capacités C_9, C_ajust, C_11, C_12, les capacités base-collecteur des transistors et les deux varactors D2 et D3. | ||
| + | (Lors de son utilisation, le varactor -ou diode varicap - est polarisée en inverse, | ||
| + | elle fonctionne alors comme un condensateur dont la capacité est ajustable selon la tension négative appliquée sur la diode.) | ||
| + | |||
| + | '''Cross-coupled VCO''' | ||
| + | |||
| + | Le VCO que nous utilisons est proche du fonctionnement d'un multivibrateur astable. | ||
| + | L'idée est que les deux transistors Q1 et Q2 fonctionnent en commutation de sorte que lorsque l'un des deux est passant, l'autre est bloqué. | ||
| + | |||
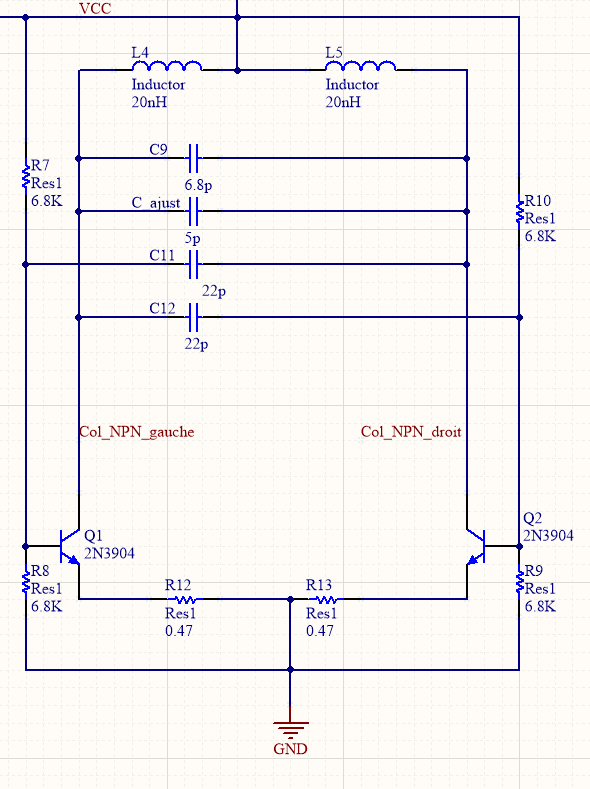
| + | Reprenons notre circuit en supprimant les varactors afin de clarifier le montage. | ||
| + | |||
| + | [[Fichier:Oscillateur_seul_topologie.PNG|500px|center]] | ||
| + | <center>''fig 8. Oscillateur couplé en crois à transistors bipolaires''</center> | ||
| + | |||
| + | Par rapport au schéma de la figure 7, la fréquence d'oscillation n'est pas seulement donnée par les valeurs des condensateurs et des inductances strictement en parallèle ( L4/L5 et C9 et C_ajust). | ||
| + | En effet, les condensateurs reliant les collecteurs et bases des deux transistors influent également ( C11 et C12 ). A ceux-ci il faut ajouter les capacités de jonction base-collecteur des deux transistors qui ne sont pas négligeables dans le calcul des capacités totales. | ||
| + | |||
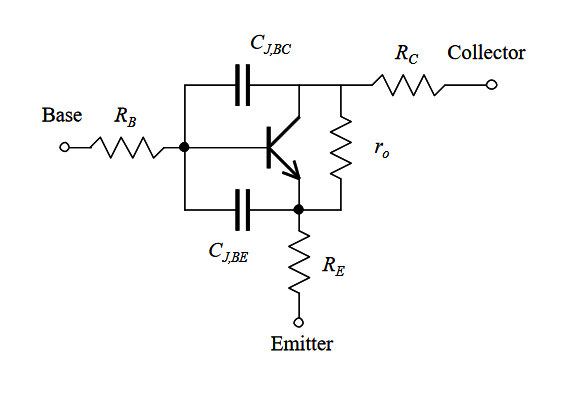
| + | En effet le modèle réel d'un transistor peut se présenter de la forme suivante : | ||
| + | |||
| + | [[Fichier:Modele_reel_BJT.PNG|500px|center]] | ||
| + | <center>''fig 9. Modèle réel d'un BJT''</center> | ||
| + | |||
| + | Dans notre cas, la capacité <math> C_{J,BC} </math> du transistor utilisé (2N3553 adéquat pour les applications d'oscillateurs en VHF) est proche de celle des capacités de base C11 et C12. | ||
| + | Cette capacité dépend de la fréquence de travail et de la voltage collecteur-base. | ||
| + | Dans le modèle SPICE que nous utilisons cette capacité est donnée par le paramètre CJC. Il vaut 34 pF. | ||
| + | |||
| + | L'idée est que la charge et décharge de ces capacités vont faire varier la tension Vbe aux bornes des transistors permettant de les faire alterner l'un et l'autre de l'état bloquant à l'état passant. | ||
| + | |||
| + | Supposons que Q2 soit passant et Q1 bloquant. La décharge des condensateurs va conduire à une hausse de tension sur la base de Q1 de sorte que lorsque la tension nécessaire est atteinte ( typiquement 0.6V) le transistor va devenir passant. Le transistor Q1 est alors saturé et ce faisant la tension VCE diminue brutalement pour descendre à 0V ( ou presque ... généralement 0,2V). | ||
| + | |||
| + | Ce brusque changement de tension va ramener les plaques de "gauche" du transistor Q1 à tension très faible inversant donc le champ à leurs bornes. Et comme C12 est relié à la fois au collecteur de Q1 et de la base de Q2, ce brusquement changement va diminuer la tension Vbe de Q2 pour le faire passer en état bloquant et le cycle continue.. | ||
| + | Pour un exemple d'un multivibrateur astable fonctionnant avec un circuit RC, voir [https://www.electronics-tutorials.ws/waveforms/astable.html] | ||
| + | |||
| + | La fréquence de résonance de notre système dans ces conditions est donnée par formule suivante | ||
| + | tirée de l'article [https://www.researchgate.net/publication/306913803_Comparative_analysis_of_differential_colpitts_and_cross-coupled_VCOs_in_180_nm_Si-Ge_HBT_technology] | ||
| + | |||
| + | <math> f_{osc} \approx \frac{1}{2\pi\sqrt{L(2C_A+C_B)}}</math> | ||
| + | |||
| + | où | ||
| + | |||
| + | <math> C_A = \frac{2C_{J,BC}C_b}{C_{J,BC}+C_b}\ ,\ C_B=2C_{parall\grave{e}le}</math> | ||
| + | |||
| + | et | ||
| + | |||
| + | <math> C_b = C_{11} \ ou \ C_{12}\ ,\ C_{parall\grave{e}le} = C_{ajust} + C_9 </math> | ||
| + | |||
| + | |||
| + | avec les valeurs de la figure 8 et en supposant que la capacité de jonction base-collecteur | ||
| + | vaut 34,6 pF à notre fréquence de travail on a : | ||
| + | |||
| + | <math> C_A = \frac{2.34,6.10^{-12}.22.10^{-12}}{34,6.10^{-12}+22.10^{-12}}=26,9pF</math> | ||
| + | |||
| + | et | ||
| + | |||
| + | <math> C_B=2.11,8.10^{-12}=23.6pF</math> | ||
| + | |||
| + | soit: | ||
| + | |||
| + | <math> f_{osc_{theorique}} \approx \frac{1}{2\pi\sqrt{40nH(2.26,9pF+23,6pF)}} \approx 90Mhz</math> | ||
| + | |||
| + | |||
| + | La simulation donne : | ||
| + | |||
| + | [[Fichier:Fig_8_config_Cparallele_12pF.PNG|1000px|center]] | ||
| + | <center>''fig 10. Simulation configuration figure 8, <math> C_{parall\grave{e}le}=11.8pF</math>''</center> | ||
| + | |||
| + | En calculant la période à l'aide des curseurs, on trouve : | ||
| + | |||
| + | <math> 5T = 659 - 606 ns </math> | ||
| + | |||
| + | soit | ||
| + | |||
| + | <math> f_{osc_{simulation}}= \frac{5.10^9}{659-606}=94Mhz</math> | ||
| + | |||
| + | |||
| + | |||
| + | <br><br> | ||
| + | En modifiant la valeur de <math>C_{parall\grave{e}le}</math> à 36.8 pF on obtient : | ||
| + | |||
| + | <math> f_{osc_{theorique}} \approx \frac{1}{2\pi\sqrt{40nH(2.26,9pF+73,6pF)}} \approx 70Mhz</math> | ||
| + | |||
| + | La simulation donne dans ce cas : | ||
| + | |||
| − | + | [[Fichier:Fig_8_config_Cparallele_37pF.PNG|1000px|center]] | |
| − | + | <center>''fig 11. Simulation configuration figure 8, <math> C_{parall\grave{e}le}=36.8pF</math>''</center> | |
| + | <math> 5T = 673 - 603 ns </math> | ||
| + | |||
| + | soit | ||
| + | |||
| + | <math> f_{osc_{simulation}}= \frac{5.10^9}{673-603}=71Mhz</math> | ||
| + | |||
| + | En modifiant les valeurs des condensateurs des jonctions base-collecteurs on peut trouver des fréquences variant de plusieurs Mhz. Il faut donc veiller à lire attentivement les datasheet | ||
| + | des transistors pour prévoir les valeurs de ces capacités( on veillera à prendre un transistor de puissance convenable, les puissances mises en jeu étant assez élevées !) | ||
| + | |||
| + | Le système de la figure 8 ne constitue qu'un oscillateur. Si on revient sur la topologie de notre émetteur, on voit apparaître en parallèle des deux condensateurs C_ajust et C_9 les deux varactors D2 et D3. C'est la propriété de ces varicap qui va nous permettre de transformer notre oscillateur en un oscillateur-mélangeur (!). | ||
| + | Expliquons. | ||
| + | |||
| + | Le signal préaccentué provenant de la section basse fréquence passe d'abord par la capacité de liaison C3. | ||
| + | La résistance R11 permet d'appliquer aux diodes varicap le signal préaccentué. | ||
| + | Ainsi le signal pré-accentué va fixer un certain potentiel sur la cathode des deux varactors. Suivant l'amplitude du signal la variation de la capacité des deux diodes sera plus ou moins importante, or ces capacités viennet s'ajouter à ceux de Cajust et C9, la fréquence d'oscillation sera donc modifié. | ||
| + | |||
| + | L'oscillateur fonctionne donc à présent en mélangeur, la résistance R4 permettant de régler l'amplitude du signal appliqué aux bornes de D2 et D3, on règle ainsi l'excursion en fréquence. | ||
| + | |||
| + | ===Application du signal modulé à l'antenne=== | ||
| + | |||
| + | La récupération de l'onde modulé se fait par couplage inductif, la seconde self L2, elle-même reliée à l'antenne tout en étant imbriquée dans L3 (voir figure 5), captant le champ électromagnétique émis par L3 : Les deux selfs constituent une sorte d'auto-transformateur. | ||
| + | |||
| + | Pour réaliser les selfs L3 et L2 qui sont de valeur très faible, on peut utiliser des fils | ||
| + | électriques " domestiques " et ce, pour plusieurs raisons : | ||
| + | |||
| + | 1. Le nombre d'enroulements est très réduit puisque les inductances sont de très faibles valeurs. On peut donc prendre des "gros fils".<br> | ||
| + | 2. L'isolation des fils va permettre d'enrouler un fil à l'autre afin de réaliser le couplage magnétique<br> | ||
| + | 3. On limite les pertes ohmiques des inductances ( rappelons-le , la résistance d'un fil est donnée par : <math> R = \rho*\frac{l}{S} </math> donc plus la section est important plus les pertes dans le fil sont minimisées).<br> | ||
| + | Le risque est que la longueur du fil ne fasse office d'antenne et que des ondes parasites soient captées ça et là. | ||
| + | |||
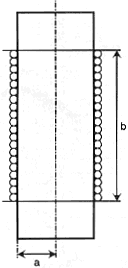
| + | Pour les selfs que nous allons réaliser, à air et à une seule couche, la formule la plus connue et la plus précise est celle dite de Nagaoka [http://www.tavernier-c.com/bobinages.htm]. | ||
| + | |||
| + | |||
| + | [[Fichier:Bobinefig1c.gif|thumb]] | ||
| + | <math> L = \frac{(0.0395 *a^2*n^2*k)}{b} </math> | ||
| + | |||
| + | où | ||
| + | |||
| + | a : rayon de la bobine en cm. <br> | ||
| + | b : longueur de la bobine en cm<br> | ||
| + | n : nombre de spires<br> | ||
| + | L : inductance en µH<br> | ||
| + | k : coefficient donné par la relation <math> \frac{2a}{b} </math><br> | ||
| + | |||
| + | En prenant un enroulement de 5 spires, une longueur totale de 3 cm, un rayon de 0,4 cm on obtient : | ||
| + | |||
| + | <math> \frac{2a}{b}=\frac{0.8}{3} = 2.67 \to k=0.9 </math><br> | ||
| + | <math> L = \frac{(0.0395 *0.4^2*5^2*0.9)}{3} = 0.047 uH = 47nH</math> | ||
| + | |||
| + | Il est à noter toutefois que cette valeur est donnée avec une approximation de 20% sans compter les approximations lors du montage. C'est pourquoi le condensateur C_ajust de la figure 5 est un condensateur variable : il permettra de fixer la fréquence central de la porteuse. Cependant, ces condensateurs n'ont pas une plage de variation infinie, c'est pourquoi il est important de bien dimensionner la bobine. | ||
| + | |||
| + | Pour la réalisation pratique, on peut utiliser un foret de 3mm de rayon et du fil de cuivre de 1.5 ou 2 mm². La gaine fait un peu moins d'un millimètre d'épaisseur ce qui réduira un peu la valeur de l'inductance.. On enroule d'abord L3 puis on vient intercaler L2 entre les enroulements de L3. Il faut ensuite faire une petite entaille au milieu L3 que l'on reliera à Vcc ( d'où la modélisation de L3 à l'aide de deux inductances L4 et L5 ) | ||
| + | |||
| + | [[Fichier:Inductances_couplees.jpg|200px]] | ||
| + | [[Fichier:Inductances_couplees_entaille.jpg|200px]] | ||
| + | |||
| + | ''fig 12. auto-transformateur "maison"'' | ||
| + | |||
| + | On pourrait ensuite caractériser cet auto-transformateur "maison" mais on peut être déjà assuré que le rendement ne sera pas de 1! | ||
| + | |||
| + | ===Simulation système complet=== | ||
| + | |||
| + | La simulation du système complet a été effectué sous Mixed Sim à l'aide d'Altium. | ||
| + | Pour cette simulation nous avons considéré d'une part que les inductances avaient une valeur un peu inférieur à celles que nous avons calculé et avons considéré que l'auto-transformateur n'était pas | ||
| + | parfait ( inductance de fuite assez importante ). | ||
| + | |||
| + | La simulation a été réalisé avec les modèles SPICE des transistors 2N3553, avec une inductance L3 valant 30 nH, L2 valant 30 nH, un coefficient de couplage entre les inductances de 0,7, et une valeur de C_ajust de 30 pF. | ||
| + | |||
| + | |||
| + | [[Fichier:88_3Mhz_output_36.8pF_induc20nh_20_nh.PNG|1000px|center]] | ||
| + | <center>''fig 12. signal de sortie de L2 non découplé à 89 Mhz''</center> | ||
| + | |||
| + | Le signal qui attaque l'antenne a donc une amplitude de 30V et une fréquence de 89Mhz. | ||
| + | La valeur de C_ajust est volontairement fixé à 30 pF puisque nous savons que sa valeur peut varier entre 5pF et 30pF. Si on diminue la valeur de C_ajust, on augmentera la fréquence de la porteuse. Donc a priori notre signal modulé se situera bien dans la bande FM avec comme minimum une fréquence de 88Mhz. | ||
== Semaine 3== | == Semaine 3== | ||
| + | |||
| + | === Oscillateur de réception=== | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ====Conditions d'oscillation==== | ||
| + | |||
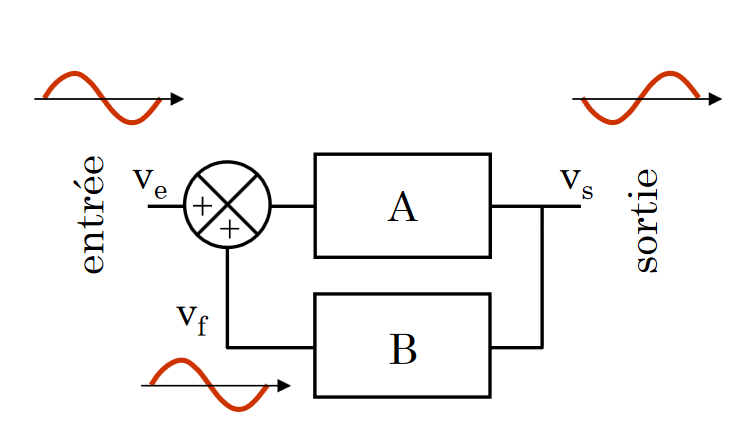
| + | Le schéma fonctionnel ci-dessous présente la structure générale d'un oscillateur. | ||
| + | |||
| + | [[Fichier:Synoptique_oscillateur.PNG|center]] | ||
| + | <center>'' fig 13. schéma fonctionnel d'un oscillateur quelconque''</center> | ||
| + | |||
| + | La structure d’un oscillateur peut se ramener à celle d’un système bouclé (ou en boucle fermée) constitué par:<br> | ||
| + | -Une chaîne directe ou d’action de fonction de transfert A(p).<br> | ||
| + | -Une chaîne de retour ou de réaction de transmittance B(p).<br> | ||
| + | -Un comparateur qui réalise la différence entre le signal d’entré et la partie du signal de sortie réinjectée à l’entrée. | ||
| + | |||
| + | La fonction de transfert d'un tel système s'écrit : | ||
| + | |||
| + | <math> T(p) = \frac{V_s(p)}{V_e(p)}=\frac{A(p)}{1+A(p)B(p)}\Rightarrow A(p)V_e(p) = [1+A(p)B(p)]V_s(p) </math> | ||
| + | |||
| + | Lorsque le signal d'entrée Ve(t) est nul, on a alors: | ||
| + | |||
| + | <math>[1+A(p)B(p)]V_s(p) = 0 </math> et pour que <math> V_s(p) \ne 0 </math>, il faut que : | ||
| + | |||
| + | <math>1+A(p)B(p) = 0 \Rightarrow A(p)B(p) = -1 </math> d'où le critère de Barkhausen ou '''condition d'auto-oscillation''' | ||
| + | |||
| + | {| style="border: 5px double grey;" | ||
| + | ||<math> | ||
| + | |||
| + | A(j\omega)B(j\omega) = -1 \Rightarrow | ||
| + | \begin{cases} | ||
| + | Re[A(j\omega)B(j\omega)]\, = -1 \quad \Leftrightarrow \ \ ||A(j\omega)B(j\omega)||= 1\\ | ||
| + | Im[A(j\omega)B(j\omega)] = 0 \quad \qquad \quad Arg[A(j\omega)B(j\omega)] = \pi +2k\pi | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |} | ||
| + | |||
| + | Dans la pratique, la condition d'accrochage de l'oscillateur est obtenue lorsque <math>||A(j\omega)B(j\omega)||</math> est légèrement supérieur à 1. L'amplitude est ensuite limité par la saturation des composants de sorte que les oscillations ne divergent pas. | ||
| + | |||
| + | ====Topologie==== | ||
| + | |||
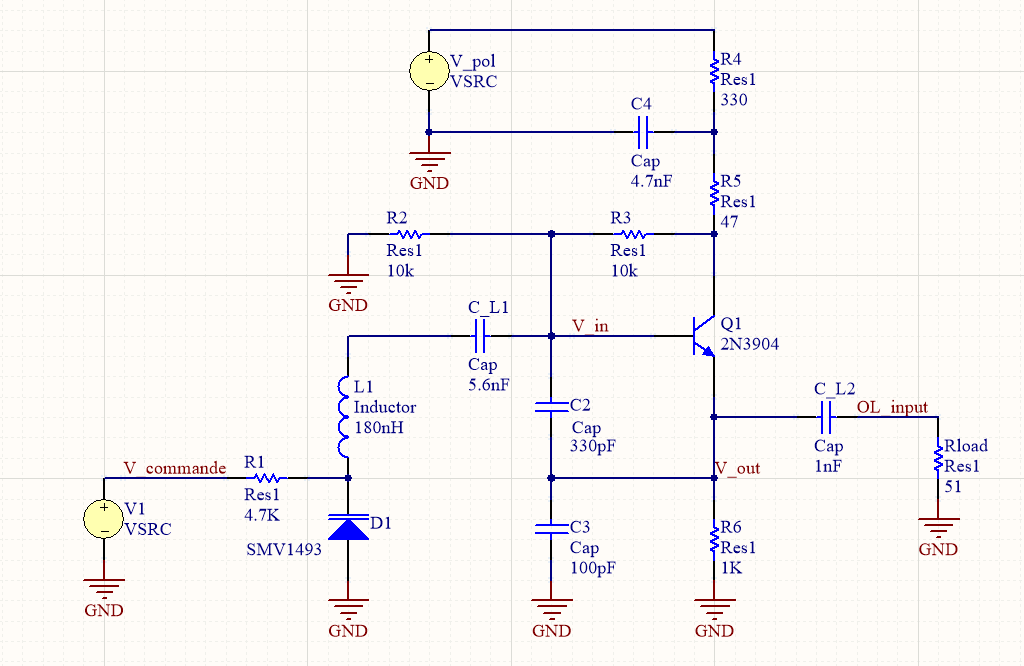
| + | Ci-dessous figure la topologie d'un oscillateur de Clapp dont les paramètres ont été choisi de telle sorte que la tension de commande permette de couvrir l'ensemble de la bande FM. | ||
| + | |||
| + | [[Fichier:Topologie_oscillateur_Clapp.PNG|center|800px]] | ||
| + | <center>''fig 14. Topologie d'un oscillateur de Clapp à BJT'' </center> | ||
| + | |||
| + | |||
| + | Le montage ci-dessus est celui-ci d'un collecteur commun (!). En effet le potentiel de référence pour la polarisation correspond bien au potentiel entre R3 et R5, les résistances R4 et R5 abaissant simplement la tension issue de V_pol.( J'ai quelque peu modifié le schéma d'origine, les résistances R4 et R5 servent peut-être seulement de diviseur de tension de sorte que la polarisation soit particulièrement précise, ou alors le concepteur initiale n'avait qu'une alimentation de 9 Volts sous la main... ).<br> | ||
| + | L'émetteur est ici relié à la charge à piloter mais on peut aussi récupérer le signal sur le collecteur, les simulations sont concluantes dans les deux cas. | ||
| + | |||
| + | L'étage d'amplification est réalisé à partir d'un transistor bipolaire, ici de type 2n3904 et d'un circuit de type LC constitué par l'inductance L1, les capacités C2 C3 et celle du varactor. | ||
| + | La capacité de liaison C_L1 empêche la tension de commande ( continue ) de venir perturber la polarisation du transistor. Elle est en série avec la varicap et de valeur beaucoup plus grande que celle de D1. C'est pourquoi sa contribution ne sera pas prise en compte dans les calculs à venir.<br> | ||
| + | La conception du circuit doit prendre en compte certains paramètres de façon à limiter au maximum le bruit de phase de l'oscillateur et ainsi améliorer la pureté spectrale du signal : <br> | ||
| + | 1.Transistor doit présenter un faible bruit<br> | ||
| + | 2.Q du circuit LC doit être le plus grand possible ( celui-ci détermine la sélectivité du circuit LC : plus il est grand plus les variation de fréquence seront faibles )<br> | ||
| + | 3.Les amplitudes des oscillations doivent être assez élevées, elles doivent toutefois restées nettement inférieures à la tension de commande qu'on applique à la diode, C'est pourquoi on utilise souvent des diodes de plusieurs dizaines de Volt de façon à limiter les fluctuations de la capacité de la diode <br> | ||
| + | |||
| + | D'autre part, un paramètre '''primordial''' dans la conception du VCO consiste en la calibration du circuit LC de façon à déterminer la '''bande couverte''' : le couplage du varactor au circuit LC doit être réalisé de sorte que le VCO délivre toutes les fréquences que nous souhaitons entre F_max et F_min. | ||
| + | |||
| + | ====Caractérisation de l'oscillateur Clapp==== | ||
| + | |||
| + | L'objectif de cette partie est de déterminer les conditions et la fréquence d'oscillation. | ||
| + | |||
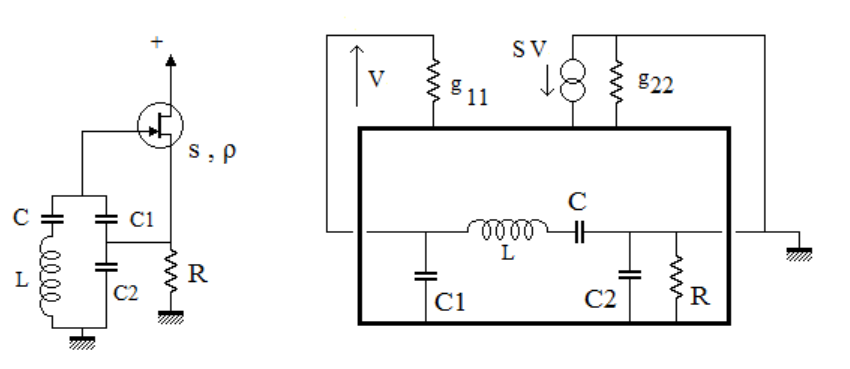
| + | L'exemple est donné dans le schéma suivant avec un FET, on considère bien sûr qu'il s'agit d'un bjt ( pour les calculs, g11, l'admittance d'entrée du transistor n'est pas nulle avec un bipolaire ). En gras le circuit source (émetteur) du transistor. | ||
| + | |||
| + | [[Fichier:Schema_equivalent_collecteur_commun.PNG|600px|center]] | ||
| + | <center>''fig 15. schéma équivalent d'un oscillateur de Clapp en collecteur commun''</center> | ||
| + | |||
| + | le schéma équivalent du transistor correspond à la chaîne d'action et celle du bas | ||
| + | au circuit de réaction. Les deux quadripôles sont montés en parallèle de sorte que les matrices d'admittance des deux quadripôles peuvent d'additionner pour former le système global. | ||
| + | Et le système oscille à condition que le '''déterminant''' de cette matrice soit nul. | ||
| + | Expliquons ce dernier point. | ||
| + | |||
| + | Si on reprend le schéma en bloc de la figure 13, on peut remarquer que les courants d’entrée et de sortie de celui-ci doivent être nuls : en effet le montage est autonome (au sens des petits signaux) et ne reçoit donc pas de signal en entrée, ni n’en fournit en sortie. | ||
| + | |||
| + | C'est-à-dire, en notant Y la matrice du système global, Ya la matrice du quadripôle du transistor et Yb celle du quadripôle du circuit LC : | ||
| + | |||
| + | <math> Y = Y_a + Y_b </math><br> | ||
| + | <math> I = YV</math><br><br> | ||
| + | <math> Y = \begin{pmatrix} Y_{11} & Y_{12} \\ | ||
| + | Y_{21} & Y_{22} | ||
| + | \end{pmatrix} | ||
| + | </math> | ||
| + | |||
| + | <math> \begin{pmatrix} I_e \\ | ||
| + | I_s | ||
| + | \end{pmatrix} | ||
| + | = | ||
| + | \begin{pmatrix} Y_{11} & Y_{12} \\ | ||
| + | Y_{21} & Y_{22} | ||
| + | \end{pmatrix} | ||
| + | \begin{pmatrix} V_e \\ | ||
| + | V_s | ||
| + | \end{pmatrix} | ||
| + | </math> | ||
| + | |||
| + | avec, | ||
| + | <math> \begin{pmatrix} I_e \\ | ||
| + | I_s | ||
| + | \end{pmatrix} | ||
| + | = | ||
| + | \begin{pmatrix} 0 \\ | ||
| + | 0 | ||
| + | \end{pmatrix} | ||
| + | </math> on obtient, | ||
| + | |||
| + | <math> | ||
| + | \begin{cases} | ||
| + | 0 = Y_{11}V_e + Y_{12}V_s \\ | ||
| + | 0 = Y_{21}V_e + Y_{22}V_s | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | Ce qui conduit à | ||
| + | |||
| + | <math> Y_{11}Y_{22} - Y_{12}Y_{21} = 0 </math> | ||
| + | |||
| + | C'est-à-dire à<br> <math> det(Y)=0 </math> | ||
| + | |||
| + | |||
| + | Un article très détaillé donnes tous les développements des calculs ( assez lourds ) menant aux résultats suivants. Il est disponible à l'adresse [http://physique-maennel.pagesperso-orange.fr/wa_files/8_20Th_C3_A9orie_20des_20oscillateurs_20v4.pdf] (se référer aux pages 100-104). | ||
| + | |||
| + | avec les notations de la topologie de la figure 14, on définit : | ||
| + | |||
| + | <math> \omega_0^2 = \frac{C_2C_3+C_{D1}C_2+C_{D1}C_3}{LC_{D1}C_2C_3}</math> | ||
| + | |||
| + | en régime permanent, la fréquence d'oscillation est donnée par : | ||
| + | |||
| + | <math> | ||
| + | \omega_{osc}^2 = \frac{1}{2} | ||
| + | \left( | ||
| + | \omega_0^2 + | ||
| + | \frac{g_{11}G}{C_2C_3} + | ||
| + | \sqrt{\left( \omega_0^2 + \frac{g_{11}G}{C_2C_3} \right)^2 - \frac{4}{LC_{D1}}\frac{g_{11}G}{C_2C_3}} | ||
| + | \right) | ||
| + | </math> | ||
| + | |||
| + | avec g11 l'admittance d'entrée du transistor et <math>G = g_{22} +\frac{1}{R6//R_{load}} </math> (g22 étant l'admittance de sortie du transistor) | ||
| + | |||
| + | Et pour de grandes valeurs de C2 et C3, on a : | ||
| + | |||
| + | <math> | ||
| + | \omega_{osc} \approx \omega_0 \sqrt{ 1 + \frac{g_{11}G(C_2+C_3)}{L\omega_0 ^4C_2^2C_3^2} } \approx \omega_0 = \sqrt{\frac{1}{L} \left( \frac{1}{C_{D1}}+\frac{1}{C_2}+\frac{1}{C_3}\right)} | ||
| + | </math> | ||
| + | |||
| + | En notant s la transconductance du transistor ( ou la pente du transistor en régime dynamique) | ||
| + | |||
| + | La condition d'oscillation est donnée par : | ||
| + | |||
| + | <math> s \geq G\frac{C_2}{C_3} + g_{11} \frac{C_3}{C_2} </math> | ||
| + | |||
| + | la transconductance s est fonction du courant de collecteur Ic, on peut donc chercher à minimiser la puissance consommée en diminuant le courant de collecteur en considérant s comme une fonction de C2 et C3 et en cherchant | ||
| + | |||
| + | <math> min(s(C_2,C_3)) = min \left( G\frac{C_2}{C_3} + g_{11} \frac{C_3}{C_2} \right) </math> | ||
| + | |||
| + | ce qui conduit à | ||
| + | |||
| + | <math> \frac{C_2}{C_3} = \sqrt{\frac{g_{11}}{G}}</math> | ||
| + | |||
| + | ie | ||
| + | |||
| + | <math> s_{opt} = 2 \sqrt{Gg_{11}}</math> | ||
| + | |||
| + | Le rapport entre C2 et C3 est donc primordial dans un tel montage, il faut tacher de les équilibrer tout en veillant à ce que ces deux capacités soient très grandes devant Cd1. | ||
| + | |||
| + | ====Modèle pour le varactor ==== | ||
| + | |||
| + | Encore une fois, l'oscillateur Clapp que nous utilisons pour réaliser notre oscillateur utilise | ||
| + | un varactor ( varicap ) dont la capacité varie en fonction de la tension inverse appliquée à | ||
| + | ses bornes. Le modèle de varactor que nous recherchons doit avoir le ratio C_max/C_min le plus élevé possible. | ||
| + | D'après l'équation de la fréquence d'oscillation et en supposant que les condensateurs formant le diviseur capacitif soient grands devant la valeur du condensateur | ||
| + | de la diode, on pourra obtenir une plus grande plage de fréquence en choisissant un | ||
| + | varactor dont le ratio est grand. D'autre part, la plage de tension sous laquelle le varactor | ||
| + | peut opérer est à prendre en considération. Par exemple les varactors de la série BBYXX ont des capacités | ||
| + | variables pour des valeurs de tension de 0 à 30 Volts. Dans notre cas, avec une alimentation de 12V il vaut mieux | ||
| + | utiliser un varactor fonctionnant sous 0/12 Volts pour éviter de rajouter un élévateur de tension au montage. | ||
| + | |||
| + | Nous avons pris le modèle SMV1493. Pour simuler convenablement un tel composant il faut créer | ||
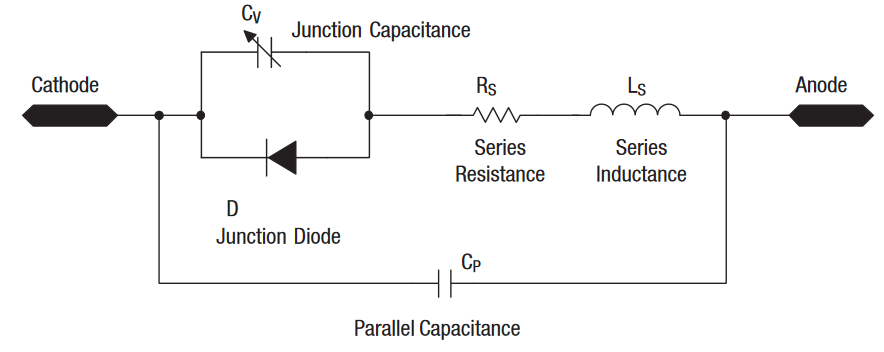
| + | son modèle SPICE. Référons-nous d'abord au circuit équivalent du varactor. | ||
| + | |||
| + | [[Fichier:Schema_equivalent_simplifie_varactor.PNG|center]] | ||
| + | <center>''figure 16. Circuit équivalent simplifié d'un varactor''</center> | ||
| + | |||
| + | Le modèle SMV1493 comprend une inductance Ls de 1,7 nH, une résistance Rs maximale de 0,5 ohms ( grandeur variant avec la fréquence ) et la capacité Cp du boîtier (négligeable ici). | ||
| + | |||
| + | La caractéristique approchée de la capacité de jonction est donnée par la relation : | ||
| + | |||
| + | <math> C_V = \frac{C_{J0}}{(1+\frac{V_R}{V_J})^M} +C_P </math> | ||
| + | |||
| + | où | ||
| + | |||
| + | <math> | ||
| + | \begin{align} | ||
| + | C_V\ &:\ capacit\acute{e}\ de\ jonction \qquad \ \ \ \ \ C_{J0}\ :\ capacit\acute{e}\ de\ jonction\ \grave{a}\ V=0 \\ | ||
| + | V_J\ &:\ potentiel\ de\ jonction \qquad \,\ \ \ \ \ C_{p}\ :\ capacit\acute{e}\ du\ boitier \\ | ||
| + | V_R\ &:\ voltage\ inverse\ appliqu\acute{e}\qquad \ M\ :\ coefficient | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | Avec notre modèle, les paramètres sont les suivants : | ||
| + | |||
| + | <math> | ||
| + | \begin{align} | ||
| + | C_{J0}\ &=\ 29\\ | ||
| + | V_J\ &=\ 0.63 \\ | ||
| + | C_{p}\ &=\ 0.10\\ | ||
| + | M\ &=\ 0.47 | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | Les tests empiriques fournis par la fiche technique et le tracé de la caractéristique approchée sont relativement proche pour considérer le modèle comme bon. | ||
| + | |||
| + | |||
| + | <center>[[Fichier:SMV1493_caracteristique_capacite_modele_approche.PNG|600px]] | ||
| + | [[Fichier:SMV1493_caracteristique_capacite_datasheet.PNG|750px]]</center> | ||
| + | <center>''fig 17. données empiriques et caractéristique approchée de la capacité du SMV1493''</center> | ||
| + | |||
| + | ==== Simulation ==== | ||
| + | |||
| + | |||
| + | Le modèle Spice réalisé pour le SMV1493 est donc<br> | ||
| + | .MODEL SMV1493 D (IS=1E-14 N=1 RS=0.5 XTI=3 EG=1.11 CJO=29E-12 M=0.47 | ||
| + | + VJ=0.63 FC=.5 BV=45.12 IBV=.1232 TT=0) | ||
| + | |||
| + | Les simulations ont été réalisées en ajoutant en parallèle avec le varactor un condensateur C_commande de valeur 6.8pF de façon à stabiliser la valeur de la capacité totale ( autrement les variation de la tension RF aux bornes du | ||
| + | varactor induisent des variations de capacité importantes et par conséquent de fréquence d'oscillations. ) | ||
| + | |||
| + | Pour la simulation les valeurs de certains composants ont été modifiés par rapport au schéma de la figure 14. | ||
| + | C2 vaut 180 pF, C3 vaut 100pF et L 150nH. | ||
| + | |||
| + | En faisant varier la tension de commande sur le varactor, on obtient: | ||
| + | |||
| + | 78Mhz pour V_commande = 0V<br> | ||
| + | 111Mhz pour V_commande = 10V<br> | ||
| + | Il est toutefois à noter qu'avec un tel système, les plus basses fréquences sont plus sensibles aux variations de fréquences que les plus grandes. En effet | ||
| + | les variations de la valeur de capacité du varactor sont plus intenses pour des tensions faibles, quand on approche de la tension maximale 10V, les variations sont beaucoup plus faibles et n'influent plus | ||
| + | beaucoup sur la capacité. On pourra également utiliser un condensateur variable pour C2 et C3 lors de la réalisation de façon à régler manuellement et à affiner les fréquences désirées. | ||
| + | |||
| + | === Filtre d'accord de réception=== | ||
| + | |||
| + | Le rôle de cette fonction électronique est de sélectionner la fréquence reçue sur l'antenne. En effet si nous ne filtrons pas l'ensemble | ||
| + | des signaux que reçoit l'antenne nous pouvons faire face aux problème de la '''fréquence image''' lors de la démodulation. | ||
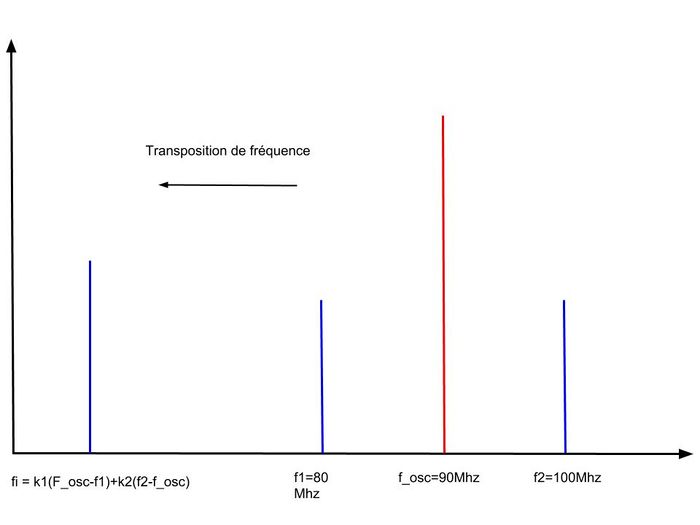
| + | Supposons que nous souhaitons démoduler un signal dont la porteuse a une fréquence de f1=80Mhz vers une fréquence intermédiaire de fi=10Mhz. | ||
| + | Imaginons que l'antenne reçoit également un signal à la fréquence f2=100Mhz. Dans ce le mélangeur opérera la démodulation sur les '''deux signaux'''. | ||
| + | Notre fréquence intermédiaire sera donc composée d'un mélange deux signaux portées par les fréquences f1 et f2 ! ( et nous ne voulons pas ça ...) | ||
| + | |||
| + | |||
| + | [[Fichier:Demodulation_frequence_spectre.jpg|700px|center]] | ||
| + | <center>''figure 17. Démodulation de fréquence : problème de la fréquence image''</center> | ||
| + | |||
| + | |||
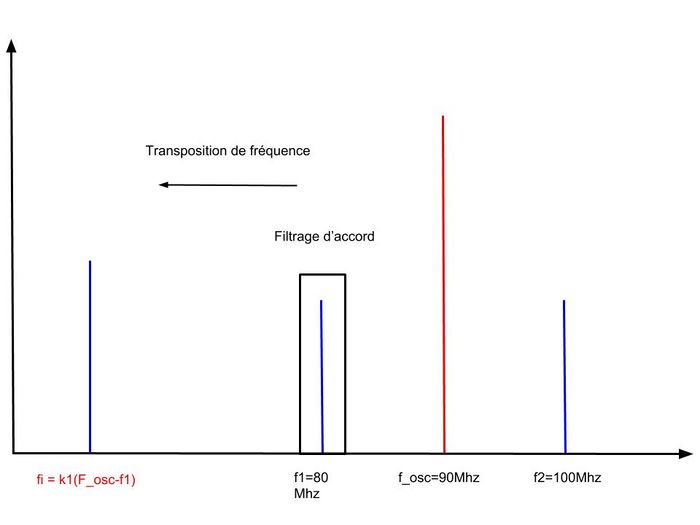
| + | Pour pallier le problème, il suffit de sélectionner '''avant''' d'effectuer la démodulation la fréquence désirée. | ||
| + | Pour cela on utilise un filtre d'accord qui sera reliée à la fréquence de l'oscillateur local. | ||
| + | |||
| + | [[Fichier:Demodulation_frequence_spectre_2.jpg|700px|center]] | ||
| + | <center>''figure 18. Démodulation de fréquence sans fréquence parasite''</center> | ||
| + | |||
| + | La difficulté dans la conception de ce filtre est qu'il doit suivre exactement les mêmes variations que l'oscillateur local que nous avons réalisé ( oscillateur de Clapp vu précédemment ). | ||
| + | On rappelle qu'en première approximation, la fréquence d'oscillation de l'oscillateur de Clapp est donnée par : | ||
| + | |||
| + | <math> | ||
| + | \omega_{osc} \approx \omega_0 = \sqrt{\frac{1}{L} \left( \frac{1}{C_{D1}}+\frac{1}{C_2}+\frac{1}{C_3}\right)} | ||
| + | </math> | ||
| + | |||
| + | Il faudra donc utiliser une structure similaire à celle que nous avons utilisé pour faire l'oscillateur. | ||
| + | |||
| + | |||
| + | ====Topologie du filtre d'accord==== | ||
| + | |||
| + | == Semaine 4== | ||
| + | |||
| + | === démodulateur de fréquence à quadrature === | ||
| + | |||
| + | |||
| + | Ce démodulateur permet de mélanger deux signaux de fréquence identique mais de phase différente. | ||
| + | Celui-ci permet d'extraire le signal audio du signal de fréquence intermédiaire issu de la première démodulation. | ||
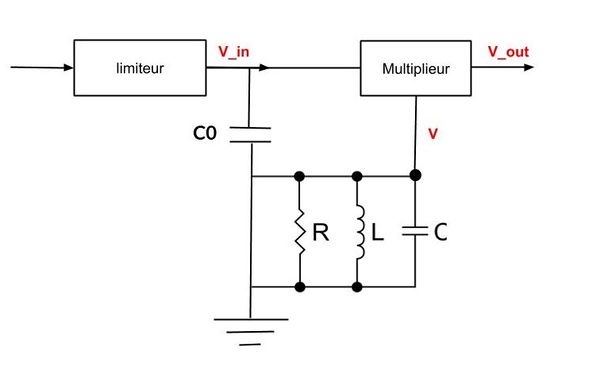
| + | Cette fonction électronique s'appuie sur un filtre déphaseur qui permet de modifier la phase du signal d'entrée V. | ||
| + | |||
| + | |||
| + | [[Fichier:Synoptique_filtre_dephaseur.jpg|600px|center]] | ||
| + | <center>''fig 4. schéma fonctionnel du récepteur''</center> | ||
| + | |||
| + | |||
| + | ==== Mise en équation ==== | ||
| + | |||
| + | |||
| + | <math>\frac{V(p)}{V_{in}(p)} = \frac{Z_{eq}(p)}{Z_{eq}(p)+Z_{C_{0}}(p)} </math> | ||
| + | |||
| + | avec | ||
| + | |||
| + | <math>Z_{eq}(p)=Z_L(p)//Z_C(p)//R </math> | ||
| + | |||
| + | <math>Z_{eq}(p)=Lp//\frac{1}{Cp}//R </math> | ||
| + | |||
| + | <math>Z_{eq}(p)=\frac{RLp}{R+RLCp^2+Lp}</math> | ||
| + | |||
| + | soit | ||
| + | |||
| + | <math>\frac{V(p)}{V_{in}(p)} = \frac{RLp}{R+RLCp^2+Lp} * \frac{1}{\frac{RLp}{R+RLCp^2+Lp}+\frac{1}{C_0p}}</math> | ||
| + | |||
| + | <math>\frac{V(p)}{V_{in}(p)} = \frac{RLp}{R+RLCp^2+Lp} * \frac{1}{\frac{RC_0Lp^2+R+RLCp^2+Lp}{(R+RLCp^2+Lp)*C_0p}}</math> | ||
| + | |||
| + | en simplifiant, | ||
| + | |||
| + | <math>\frac{V(p)}{V_{in}(p)} = \frac{RLC_0p^2}{RLC_0p^2+RLCp^2+Lp+R}</math> | ||
| + | |||
| + | <math>\frac{V(p)}{V_{in}(p)} = \frac{C_0}{C_0+C} * \frac{RLp^2}{RLp^2+\frac{L}{C_0+C}p+\frac{R}{C_0+C}}</math> | ||
| + | |||
| + | ie, | ||
| + | |||
| + | <math>\frac{V(p)}{V_{in}(p)} = \frac{C_0}{C_0+C} * \frac{1}{1+\frac{1}{R(C_0+C)p}+\frac{1}{L(C_0+C)p^2}}</math> | ||
| + | |||
| + | En posant: | ||
| + | |||
| + | <math>\omega_1 =\frac{1}{\sqrt{L(C_0+C)}}</math> | ||
| + | |||
| + | et | ||
| + | |||
| + | <math> Q =R(C_0+C)\omega_1</math> | ||
| + | |||
| + | on obtient : | ||
| + | |||
| + | |||
| + | <math>\frac{V(p)}{V_{in}(p)} = \frac{C_0}{C_0+C} * \frac{1}{1+\frac{\omega_1}{Qp}+(\frac{\omega_1}{p})^2}</math> | ||
| + | |||
| + | On cherche maintenant à déterminer le déphasage entre nos deux signaux, ce qui revient à calculer l'argument de notre fonction de transfert: | ||
| + | |||
| + | <math> \phi = \arg{T(j\omega)}=\arctan{\frac{\Im{\frac{V(j\omega)}{V_{in}(j\omega)}}}{\Re{\frac{V(j\omega)}{V_{in}(j\omega)}}}}</math> | ||
| + | |||
| + | <math>T(j\omega)= \frac{C_0}{C_0+C} * \frac{1}{1-j\frac{\omega_1}{Q\omega}-(\frac{\omega_1}{\omega})^2}</math> | ||
| + | |||
| + | <math>T(j\omega)= \frac{C_0}{C_0+C} * \frac{1-(\frac{\omega_1}{\omega})^2+j\frac{\omega_1}{Q\omega}}{(1-(\frac{\omega_1}{\omega})^2)^2+(\frac{\omega_1}{Q\omega})^2}</math> | ||
| + | |||
| + | On obtient donc : | ||
| + | |||
| + | <math> \phi = \arctan{\frac{\frac{\omega_1}{Q\omega}}{1-(\frac{\omega_1}{\omega})^2}} </math> | ||
| + | |||
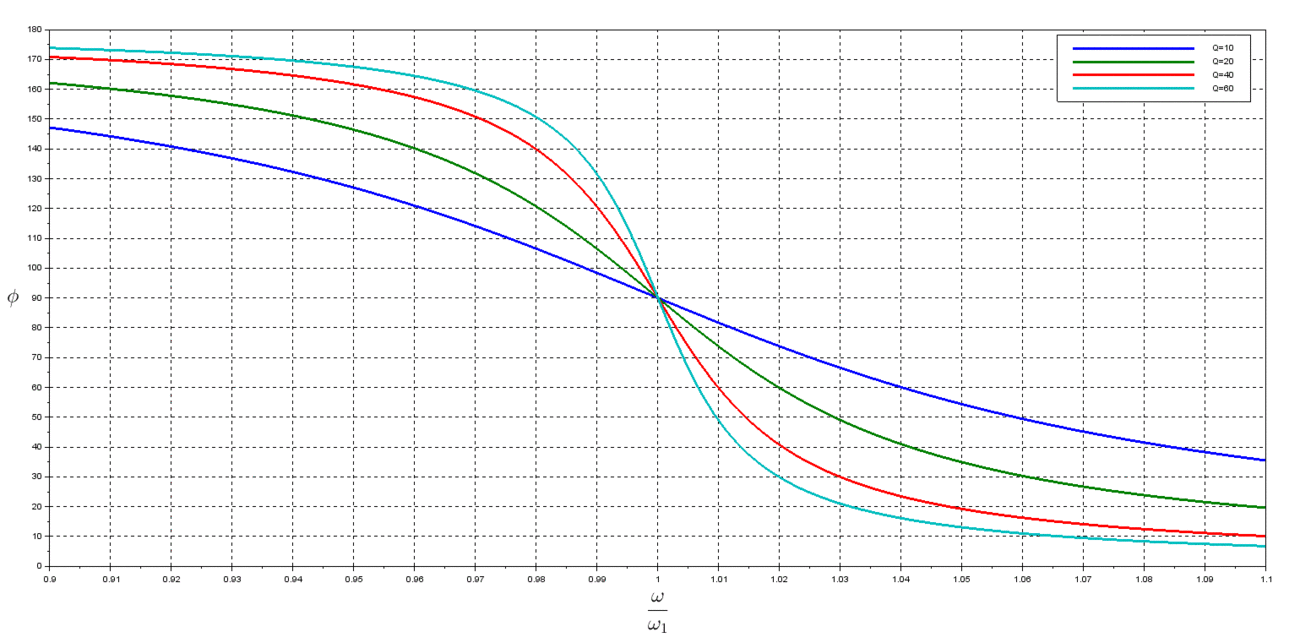
| + | Le graphe de l'argument de la fonction de transfert du filtre est donné pour différentes valeurs de Q, le facteur de qualité. | ||
| + | |||
| + | |||
| + | [[Fichier:Argument_filtre_en_fonction_pulsation_reduite.gif|1300px|center]] | ||
| + | <center>''fig ?. argument du filtre déphaseur en fonction de la pulsation réduite''</center> | ||
| + | |||
| + | On constate qu'au voisinage de 1 ( c'est-à-dire quand <math>\omega \sim \omega_1</math> ), le déphasage est d'environ <math>\frac{\pi}{2}</math> et que la réponse du filtre est proche d'une pente d'équation : | ||
| + | |||
| + | <math> \frac{\Delta\phi}{\Delta\omega} = -\frac{2Q}{\omega_1} </math> | ||
| + | |||
| + | En effet, la dérivée de la réponse est telle que : | ||
| + | |||
| + | <math> \phi' = (\arctan{\frac{\frac{\omega_1}{Q\omega}}{1-(\frac{\omega_1}{\omega})^2}})'</math> | ||
| + | |||
| + | |||
| + | Puisque, | ||
| + | |||
| + | <math> (f\circ g)' = (f'\circ g)*g' </math> | ||
| + | |||
| + | On obtient : | ||
| + | |||
| + | <math> \phi' = \frac{-(1+\frac{\omega_1}{\omega}^2)}{\frac{Q\omega^2}{\omega_1}(1-\frac{\omega_1}{\omega^2})^2+\frac{\omega_1}{Q}}</math> | ||
| + | |||
| + | <math>\frac{-(1+\frac{\omega_1}{\omega}^2)}{\frac{Q\omega^2}{\omega_1}(1-\frac{\omega_1}{\omega^2})^2+\frac{\omega_1}{Q}} \,\underset{\omega_1}{\sim}\, \frac{-2}{\frac{\omega_1}{Q}} </math> | ||
| + | |||
| + | <math>\phi'\, \underset{\omega_1}{\sim} \, \frac{-2Q}{\omega_1}</math> | ||
| + | |||
| + | Ainsi, le déphasage total de <math>V </math> par rapport à <math>V_{in}</math> sera de : | ||
| + | |||
| + | <math>\frac{\pi}{2}-\frac{2Q\Delta\omega}{\omega_1}</math> | ||
| + | |||
| + | En supposant que <math>V_{in} = Asin(\omega t)</math>, on a : | ||
| + | |||
| + | <math> V = Asin(\omega t + \frac{\pi}{2} - \frac{2Q\Delta\omega}{\omega_1})</math> | ||
| + | |||
| + | En multipliant les deux signaux, on a : | ||
| + | |||
| + | <math> V * V_{in} = A^2sin(\omega t)sin(\omega t + \frac{\pi}{2} - \frac{2Q\Delta\omega}{\omega_1})</math> | ||
| + | |||
| + | soit en utilisant les fameuses formules de trigonométrie : | ||
| + | |||
| + | <math> V * V_{in} =\frac{A^2}{2} (cos( \frac{2Q\Delta\omega}{\omega_1} - \frac{\pi}{2})+ cos(2\omega t + \frac{\pi}{2} - \frac{2Q\Delta\omega}{\omega_1}))</math> | ||
| + | |||
| + | et en filtrant la composante de plus haute fréquence, on obtient : | ||
| + | |||
| + | <math>V_{out} =\frac{A^2}{2} cos( \frac{2Q\Delta\omega}{\omega_1} - \frac{\pi}{2}) = \frac{A^2}{2} sin( \frac{2Q\Delta\omega}{\omega_1} )</math> | ||
| + | |||
| + | En supposant que <math> \Delta\omega \ll \omega_1 </math>, on obtient : | ||
| + | |||
| + | <math> V_{out} = A^2 Q\frac{\Delta\omega}{\omega_1} </math> | ||
| + | |||
| + | On rappelle que <math>\Delta\omega</math> est l'excursion en fréquence du signal dans laquelle on retrouve l'information de notre signal modulé. | ||
| + | La valeur du facteur de qualité doit faire l'objet d'une certaine attention. En effet si on choisit un Q trop élevé, la réponse du filtre pour <math> \omega = \omega_1</math> n'est plus linéaire. | ||
| + | Cependant, si on choisit une valeur de Q trop faible, l'amplitude du signal discriminé est trop faible ( voir la dernière équation ). | ||
| + | Puisque la variation de fréquence en bande FM est limité de part et d'autre de la porteuse à 75kHz, avec un filtre centré à 10,7Mhz, on a donc | ||
| + | comme valeur de pulsation normalisée maximale: | ||
| + | |||
| + | <math>u_{max} = \frac{10700 + 75}{10700} = 1.007</math> | ||
| + | |||
| + | et minimale: | ||
| + | |||
| + | <math>u_{min} = \frac{10700 - 75}{10700} = 0.993</math> | ||
| + | |||
| + | |||
| + | A l'aide de la figure !!!, on détermine graphiquement qu'une valeur de Q comprise entre 20 et 40 convient. | ||
| + | On choisira une valeur Q = 30 pour notre système. | ||
| + | |||
| + | Il faut maintenant dimensionner à partir des équations du circuit, les valeurs des composants du filtre. | ||
| + | |||
| + | ==== Dimensionnement ==== | ||
| + | |||
| + | La fonction électronique décrite ci-dessus est assurée par le SA614. | ||
| + | On sait d'ores et déjà, d'après la fiche technique que la valeur recommandée de la capacité en série <math> C_0</math> est de 1pF. | ||
| + | D'autre part, la résistance R est interne au SA614 et vaut 40kOhm. | ||
| + | Comme nous avons choisi Q = 30 ( valeur intermédiaire pour éviter la distorsion et pas trop amortir le signal à démoduler) et que <math> \omega_1 = 10,7 Mhz</math>, on détermine la valeur de la capacité C. | ||
| + | |||
| + | <math> Q = R(C_0+C)\omega_1</math> | ||
| + | |||
| + | <math> C = \frac{Q}{R\omega_1}-C_0</math> | ||
| + | |||
| + | <math> C = \frac{30}{40.10^3.2\pi.10,7.10^6} - 1.10^{-12} = 1,1155*10^{-12}pF= 10.2pF</math> | ||
| + | |||
| + | On pourra prendre un condensateur normalisé de la série E48. La valeur la plus proche est de 10pF. ( plus cher mais plus précis ... !) | ||
| + | |||
| + | On en déduit ensuite la valeur de L: | ||
| + | |||
| + | <math>\omega_1 =\frac{1}{\sqrt{L(C_0+C)}}</math> | ||
| + | |||
| + | <math>L = \frac{1}{\omega_1^2(C_0+C)} </math> | ||
| + | |||
| + | <math>L = \frac{1}{(4\pi^210,7.10^6)^2(1.10^{-12}+10.10^{-12})} =2,01.10^{-5}H= 20\mu H</math> | ||
| + | |||
| + | Une simulation du filtre avec les valeurs ci-dessus est donnée ci-dessous. | ||
| + | |||
| + | |||
| + | [[Fichier:Bode_filtre_RLC.JPG|1300px|center]] | ||
| + | <center>''fig ?. lieu de bode du filtre déphaseur''</center> | ||
| + | |||
| + | Le filtre pourrait être un peu mieux centré en ajustant la valeur de l'inductance par exemple ( ce qui est souvent fait en pratique grâce à une inductance variable ). | ||
| + | Mais on retrouve bien le déphasage de 90 degrés et la bande passante centrée en 10.7Mhz. | ||
Schémas des systèmes. | Schémas des systèmes. | ||
| Ligne 307 : | Ligne 1 082 : | ||
| − | |||
Simulation Spice émetteur | Simulation Spice émetteur | ||
Version actuelle datée du 24 février 2019 à 19:12
Sommaire
Présentation générale
Description
Cet article décrit le fonctionnement et la réalisation pratique d'un émetteur et récepteur à modulation de fréquence pour la bande de radiodiffusion commerciale de 88 MHz à 108 MHz.
Objectifs
L'objectif du projet est de réaliser à moindre coût un système de radio-diffusion dans la bande des très hautes fréquences ( very high frequency/VHF ).
L'opérateur pourra à l'aide de ce système émettre une onde HF à l'aide de la source sonore de son choix. En réception, l'opérateur pourra choisir la fréquence qu'il souhaite démodulé, en effectuant les réglages nécessaires à l'aide d'une petite commande et pourra ensuite écouter le signal démodulé à l'aide d'un petit haut-parleur.
Le système à réaliser doit être le plus performant possible en termes de qualité de signal ( rapport signal/bruit le plus faible possible ) mais doit aussi permettre d'effectuer une radiodiffusion de longue distance.
Préparation du projet
Choix techniques
La bande que nous avons choisi d'utiliser pour réaliser notre système FM est la bande de radio-diffusion des stations de "radio" dans laquelle a priori nous n'avons pas le droit d'émettre - la puissance émise doit être limitée à 50nW. Le spectre de fréquence est en effet une ressource rare et convoitée qui doit être partagée entre tous les acteurs des radio-diffusions ( GPS, Wifi, usage militaire, Radio FM...). Il est donc interdit d'émettre des ondes dans certaines bandes de fréquences afin de pas perturber le trafic.
Cependant, le choix que nous avons fait est motivé par des considérations pratiques de réalisation du projet. Dans la mesure où si nous avions utilisé la bande 144 Mhz ( désignée aussi par sa longueur d'onde : bande des 2 mètres ) qui est réservée à l'usage des radioamateurs, il aurait été plus difficile de tester séparément l'émetteur et le récepteur. En effet si l'émetteur est défectueux, il sera difficile de tester le bon fonctionnement du récepteur si aucune onde n'est émise dans la bande des 144 Mhz.Or nous savons que dans la bande 88Mhz 108Mhz, nous pouvons aisément testé le récepteur ( puisque les grandes stations émettent en continu ) et l'émetteur ( en émettant à une fréquence intermédiaire entre deux stations ).Du reste, il sera intéressant de comparer notre système de réception avec les radios commerciales; d'abord à l'écoute en comparant la pureté des signaux, ensuite en effectuant l'analyse des signaux démodulé à l'oscilloscope.
Liste des tâches à effectuer
Ce projet s'articulera autour de 5 grandes tâches à réaliser :
- Conception de l'architecture de l'émetteur et du récepteur
- Calculs des composants pour chaque fonction électronique
- Simulation des divers étages électroniques
- Réalisation du prototype de l'émetteur/récepteur
- Ajustements du système
Liste du matériel
Émetteur radio
- diodes zener
- transistors 2N2219
- diodes varicap BBY40
- ampli op TL081
- condo ajustable 6.5 30 pF
- self 47µH (alim émetteur)
- 47 kohm
- 6.8kohm
- 10kohm
- 3.3 kohm
- 1kohm
- 470 µOhm
- potentiomètres 10k (excursion émetteur )
- 18 pF
- 6.8 pF
- 22pF
- 1nF
- 10µF
- 100 nF
- 100kohms
- 220 kohms
- 120pF
Filtre RF
- diodes varicap BB202
- condensateurs ajustables 5/20 pF
- inductance 150 nH (filtre entrée récepteur)
- inductance 250 nH (filtre entrée, récepteur)
- 220 pF
Oscillateur de réception
- diodes varicap BB202
- transistors BC547
- transistors BFR92
- condensateurs ajustables 5/20 pF
- self 1 µH
- 4.7kohm
- 330 ohm
- 10kohm
- 1kohm
- 27pF
- 30pF
- 100 nF
Étage changeur de fréquence
- mélangeur
- filtres céramiques 10.7 MHz
- self 5.5 µH (alim SA612)
- 51 ohm
- 10 nF
Amplificateur limiteur / multiplieur
- système FM fi
- filtres céramiques 10.7 MHz
- inductance 180 µH (quadrature tank)
- condensateur ajustable (quadrature tank)
- 1pF (quadrature tank)
- 47 pF(quadrature tank)
- 150 pF
Amplificateur audio
- amplificateur audio
- potentiomètres 10k ( volume ampli)
Divers étages
- connecteur coaxial femelle
- régulateur de tension
- résistances 100k (Commande d'accord)
Réalisation du Projet
Prologue
Radiodiffusion : liaisons hertziennes
Dans les télécommunications, on distingue trois grandes familles de supports de transmission de l'information
- Liaisons filaires
- Liaisons optiques
- Liaisons hertziennes
L'intérêt principal des liaisons hertziennes réside dans l'absence de support physique entre l'émetteur et le récepteur. Pour des systèmes en mouvement, c'est parfaitement adéquat. Les inconvénients principaux des liaisons hertziennes résident également dans l'absence de support : puisque le milieu de transmission est partagée par tout le monde, comment faire pour que tout le monde puisse communiquer en même temps ? Cette difficulté impose une gestion stricte des fréquences. Chaque système dispose d'une bande de fréquence qui lui a été allouée.
Les recherches et évolutions technologiques concernant les liaisons hertziennes se concentrent essentiellement autour de la possibilité de transmettre un maximum d'information en occupant un minimum d'espace fréquentiel. La télévision numérique terrestre (TNT), par exemple, est une évolution technique en matière de télédiffusion, fondée sur la diffusion de signaux de télévision numérique. Par rapport à la télévision analogique terrestre à laquelle elle se substitue, la TNT permet de réduire l'occupation du spectre électromagnétique grâce à l'utilisation de modulations plus efficaces et d'obtenir une meilleure qualité d'image.
La transmission par liaison hertzienne consiste généralement à "accrocher" le signal basse fréquence ( information utile : voix, musique, vidéo... ) à une onde haute fréquence appelée porteuse. C'est l'opération de modulation.
Modulation FM vs modulation AM
Historiquement les premiers systèmes radio utilisaient la modulation d'amplitude (AM) pour transmettre les informations sonores. Le principe de la modulation d'amplitude fut découverte au milieu des années 1870 tandis que la modulation FM fut découverte dans les années 1930. La modulation AM a comme avantage de permettre une détection avec un appareil simple même si la puissance du signal n'est pas très importante. En contrepartie, même si les émetteurs utilisant ce type de modulation pouvaient transmettre les signaux sonores sur une bande de fréquence de 15kHz, les récepteurs ne permettaient généralement que de démoduler une bande de 5kHz, la richesse harmonique devient gravement amoindrie.
Le principal inconvénient de la modulation AM est que le signal est bien plus affecté par la transmission hertzienne. Le signal récupéré par le récepteur est de moins bonne qualité que dans le cas de la modulation FM. La modulation FM nécessite un système d'émission et de réception plus complexe que la modulation. Et bien que découverte en 1930, il faudra attendre les années 1990 pour que la plupart des stations de musiques abandonnent la modulation AM pour la modulation FM, permettant d'obtenir un meilleur signal en réception.
Antennes
L'antenne a un rôle très imporant dans les liaisons hertziennes, elle assure l'interface entre le circuit électronique et le milieu de propagation.
L'antenne est un dispositif réciproque:
- - En émission, l'antenne reçoit un courant et une tension, elle génère un champ électrique et un champ magnétique.
- - En réception, l'antenne reçoit un champ électrique et magnétique, elle génère tension et courant.
Le dimensionnement d'une antenne dans un système radio constitue un élément clé. En effet, dans le cas de la réception, si l'antenne n'est pas adéquate, la puissance reçue ne sera pas suffisante pour permettre au reste du circuit de l'exploiter, quand bien même les étages suivants utilisés sont particulièrement performants.
Dans le cas de l'émission, il faut optimiser la transmission de puissance entre le générateur et l'antenne.
L'impédance du générateur doit être égale à l'impédance de la ligne qui doit elle même être égale à l'impédance présentée par l'antenne. Si le système est désadapté, il existe un phénomène d'ondes stationnaires sur la ligne : une partie de l'énergie émise est réfléchie vers le générateur. On constate alors sur la ligne des minima et maxima de tension. Ainsi, pour caractériser l'impédance d'entrée de l'antenne, les constructeurs spécifient généralement le TOS ( taux d'ondes stationnaire ) de l'antenne. Le TOS représente le rapport entre la tension minimale et la tension maximale sur la ligne. plus l'impédance de l'antenne est proche de sa valeur idéale, et plus le TOS est proche de 1.
tableau TOS : Puissance réfléchie sur puissance émise.
Lors de la modélisation du système, il faut également s'intéresser à la bande passante de l'antenne. Celle-ci présente des caractéristiques optimales que dans une certaine bande de fréquence. Les dimensions de l'antenne sont liés à la longueur d'onde des ondes qu'on souhaite transmettre ou recevoir. Une antenne est donc un dipôle résonnant.
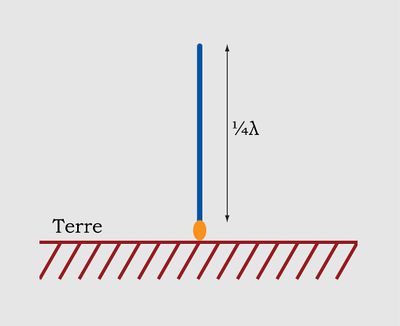
Dans notre cas, pour la bande FM, on pourra utiliser un fil en guise d'antenne filaire quart d'onde.
Puisque la bande utilisée se situe autour de 100 Mhz, la longueur d'onde moyenne est de 3 mètres. Il faut donc, pour réaliser une antenne quart d'onde, une antenne
d'environ 75 cm. Les ajustements peuvent être effectués lors de la réalisation pratique : on monte d'abord une antenne de dimension supérieur en coupant peu à peu le fil.
En coupant petit à petit le fil, on devrait constater une augmentation de la puissance reçue puis une diminution. On notera la dimension de l'antenne pour laquelle le maximum est atteint.
Bilan de liaison
Le bilan de liaison d'une liaison hertzienne permet de déterminer si le niveau de puissance reçu par le récepteur sera suffisant pour que la liaison fonctionne correctement. En effet si la puissance reçue est trop faible, le dispositif électronique de réception n'a pas la sensibilité nécessaire pour extraire le signal pertinent. La puissance reçue peut s'exprimer de la façon suivante :
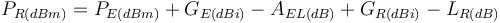
où :
'
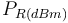 et
et 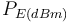 désignent la puissance reçue par le récepteur et émise par le récepteur.
désignent la puissance reçue par le récepteur et émise par le récepteur.
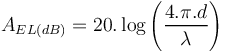 désigne l'atténuation en espace libre, avec d la distance entre émetteur et récepteur et
désigne l'atténuation en espace libre, avec d la distance entre émetteur et récepteur et 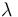 la longueur d'onde
la longueur d'onde
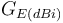 et
et 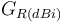 désignent les gains d'antenne.
désignent les gains d'antenne.
Le gain d'antenne traduit le fait que le rayonnement est privilégié dans une certaine direction de l'espace par rapport à une autre.
Il est défini grâce à l'antenne isotrope ( antenne inexistante qui rayonne la même puissance dans toutes les directions de l'espace ). Soit un émetteur doté d'une antenne isotrope, P0 est la puissance reçue par un récepteur.
On remplace maintenant l'antenne isotrope par une antenne directive, la puissance reçue par le récepteur est alors P1, plus importante que P0.
Le gain d'antenne vaut alors :
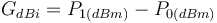
Ainsi, lorsqu'on définit la structure de notre système de communication hertzien, plusieurs paramètres sont à prendre en compte. Certaines antennes peuvent ne pas capter dans toutes les directions mais leur gain d'antenne peut augmenter la puissance reçue sur le capteur, la distance qui sépare l'émetteur et le récepteur doit être suffisante pour remplir le cahier des charges. La fréquence de fonctionnement du système doit être prise en compte également : plus la fréquence est importante et plus l'atténuation en air libre sera grande.
On veillera dans tous les cas à dimensionner convenablement les équipements et disposer d'une certaine marge pour s'assurer des éventuelles atténuations supplémentaires qui peuvent être dues à des réflexions multiples ( fading ) ou à la météo ( pluie, neige ... )
Semaine 1
Les schémas ci-dessous présentent la structure de notre système radio
Structure de l'émetteur
L'émetteur est constitué :
- 1 . d'une fonction électronique assurant la pré-accentuation.
Précisons ce dernier concept. Dans le domaine audio, la préaccentuation consiste à amplifier les fréquences aiguës à partir d'une certaine fréquence. L'amplification est de plus en plus importante au fur et à mesure que la fréquence augmente. Ce qui impose la connaissance de deux paramètres au moins :
- -paramètre indiquant à partir de quelle fréquence le système doit commencer à faire effet : cette fréquence, appelée fréquence de coupure ou fréquence de transition, correspond au point pour lequel on note une amplification du signal de +3 dB.
- -paramètre indiquant la force avec laquelle le signal traité doit être amplifié : on parle de la pente d'amplification.
La préaccentuation adoptée pour la diffusion FM n'échappe pas à cette règle. Les paramètres retenus pour cette dernière sont les suivants : - Fréquence de coupure Fc (fréquence à partir de laquelle le signal est augmenté de 3 dB) égale à environ 3180 Hz (correspondant à une constante de temps de 50 us et une pente de 6dB/octave.
La désaccentuation est le procédé inverse de la préaccentuation, qui consiste à redonner à un signal audio préaccentué, son contenu fréquentiel d'origine. Elle est assuré par le récepteur FM lors du traitement du signal.
Pourquoi accentuer les aiguës lors de la transmission FM ? D'un point de vue contenu audio pur, une préaccentuation immédiatement suivie d'une désaccentuation peut sembler ne présenter aucun intérêt. Par contre, si entre le circuit de préaccentuation et celui de désaccentuation, le signal audio passe dans un endroit "bruyant", cela permet de récupérer au bout de la chaine, un signal audio moins perturbé par le bruit généré par ses maillons
- 2 . d'un VCO (Voltage controlled oscillator)
L’oscillateur commandé en tension ou VCO est un système électronique qui génère un signal périodique dont la fréquence se stabilise en fonction de la tension d'entrée. Il existe différents types d'oscillateurs ( oscillateur RC, oscillateur LC ). Les oscillateurs RC sont davantage utilisés en basse fréquence, tandis qu'en haute fréquence, pour les systèmes de radiocommunication, on préférera utiliser des oscillateurs LC. Dans le cadre de notre émetteur/récepteur FM, nous utiliserons un oscillateur Clapp et un oscillateur rectangulaire ( ou différentiel cross coupled ... ? à voir avec les simulations ... ). La diode varicap est l'élément clé du VCO qui permet d'obtenir une variation de fréquence en fonction de la tension de commande. Une diode varicap, ou varactor, présente une capacité équivalente fonction de la tension inverse appliquée.
- 3 . d'un mélangeur
Le mélangeur est un composant électronique permettant d'assurer la fonction "changement de fréquence" en réalisant la translation du spectre de ce signal. Le mélangeur idéal est un multiplieur : il permet de multiplier deux signaux d'entrée pour obtenir en sortie un signal dont les fréquences ont été additionnées ou soustraites. Quelques formules de trigonométries s'imposent :
Soit,
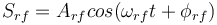
et
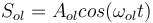
respectivement le signal modulant et le signal de l'oscillateur local.
Le mélangeur assure une opération de multiplication, on se retrouve donc en sortie avec un signal de la forme :
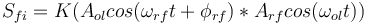
Or,
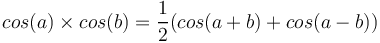
Donc,
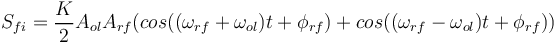
Graphiquement, on retroue les deux composantes 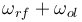 et
et 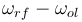 de part et d'autre de la porteuse ( l'oscillateur local).
de part et d'autre de la porteuse ( l'oscillateur local).
Il est important de noter que seule l'une des deux raies sera utilisée. On verra en quoi le problème de la fréquence image peut poser problème dans le cas de la réception.
- 4 . d'un ampli
L'amplificateur sert à délivrer la puissance désirée à l'antenne d'émission... La puissance nécessaire dépend de l'application. Par exemple, les puissances délivrées par les Modem ( liaison Wifi à 2.4Ghz ... ) sont bien plus faibles que celles des émetteurs FM qui doivent couvrir des zones bien plus importantes. Ces derniers peuvent délivrer des puissances de plusieurs dizaines de kWatts !
Structure du récepteur
Le synoptique ci-dessus présente le récepteur FM couplé à l'amplificateur audio permettant l'écoute du signal démodulé. Ce récepteur est composé de :
- 1 . d'une antenne de réception (!). Celle-ci doit encore une fois être dimensionner de telle sorte que le maximum de puissance
soit reçu sur la bande de fréquence désirée.
- 2 . d'un filtre RF. Ce filtre est censé sélectionner la bande de fréquence à démoduler. Il permet de ne présenter au premier mélangeur que la
bande désirée et ainsi d'éviter de démoduler la fréquence image.
- 3 . d'un premier mélangeur qui assure l'abaissement de fréquence vers une fréquence intermédiaire de 10.7Mhz.
- 4 . d'une commande d'accord : celle-ci permet de régler à la fois la sélectivité du filtre RF et la fréquence du VCO.
Les deux fonctions électroniques sont réglés conjointement : le circuit est donc accordé.
- 5 d'un filtre FI qui permet de ne récupérer que la nouvelle fréquence centrale issue de la transposition de fréquence ( Fi = F_rf - F_ol).
Cette fonction est assurée par un filtre céramique.
- 6 d'un amplificateur limiteur. Le détecteur FM est différent du détecteur AM, car il est sensible à la modulation de fréquence et insensible aux variations d’amplitude de la porteuse.
L'information audiofréquence étant inscrite dans la fréquence instantanée , nous pouvons amplifier et écrêter le signal FI , ce qui permettra de supprimer une grande partie des parasites qui se seront ajoutés au signal au cours de la transmission : c'est le rôle de l'amplificateur-limiteur.
- 7 d'une autre mélangeur, il s'agit d'un démodulateur de fréquence à quadrature.
L'idée par rapport à un mélangeur classique est que ce démodulateur ne mélangeur pas deux signaux de fréquence différents mais deux signaux de fréquence identique mais de phase différente.
- 8 d'un filtre passe-bas. Comme nous l'avons indiqué le signal émis a d'abord été pré-accentué. Le filtre passe-bas devra donc prendre en compte cette déformation du signal.
Ainsi, le filtre passe-bas aura sa fréquence de coupure non pas à 15kHz mais à la fréquence de coupure de l'étage de pré-accentuation, c'est-à-dire 3180 Hz.
- 9 d'un amplificateur audio classique, basé autour d'un LM386.
Semaine 2
Descriptif de l'émetteur radio
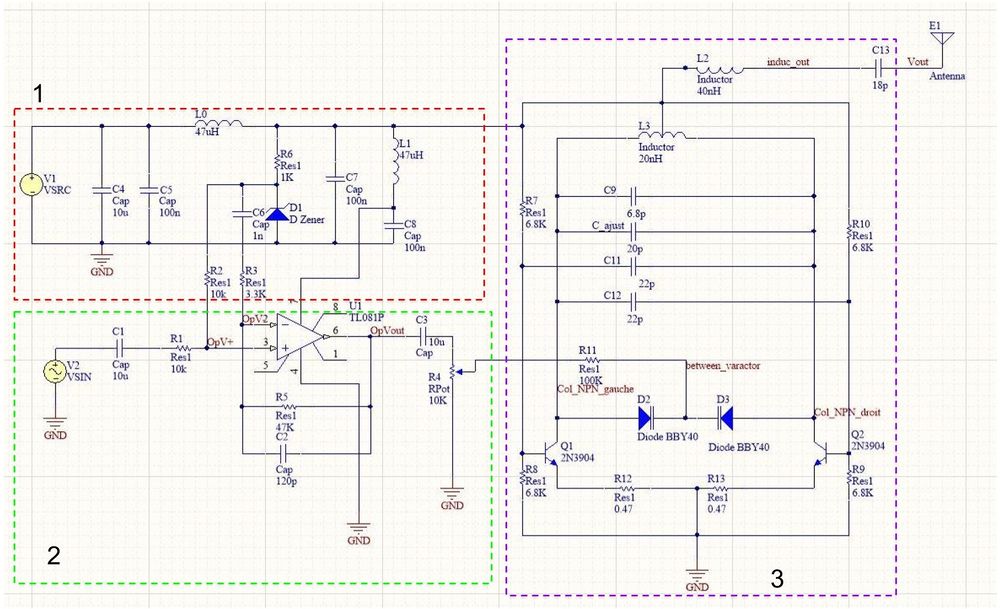
Topologie de l'émetteur
Cet émetteur s'inspire des travaux de Remy Mallard ( émetteur FM 003 https://sonelec-musique.com/ )
Alimentation du circuit
L'alimentation peut être effectuée grâce à un régulateur de tension 12V ( composant assez classique ). On notera toutefois que deux filtres passe-bas permettent de découpler la section haute fréquence des autres éléments du circuit. Ainsi, le filtre passe-bas en pi composé de de L0, C5 et C7 permet d'éviter que les signaux hautes fréquences ne viennent perturber l'alimentation. L'autre filtre passe-bas du second ordre, formé par l'inductance L1 et C8 permet d'alimenter la section BF sans la HF ne vienne perturber son fonctionnement( parmi les erreurs de simulation commises, nous avons pu remarqué qu'un signal de "moyenne fréquence" non filtré par ce filtre perturbait l'alimentation de l'ampli op et déformait complètement le signal ).
Section basse-fréquence
La première observation notable dans cette section est que l'amplificateur opérationnel choisi est doté d'une alimentation simple alors qu'a priori, le signal audio d'entrée attaque d'abord un condensateur de liaison : le signal gravite donc autour d'un potentiel de 0 Volt. Si un tel signal attaquait directement l'entrée de l'ampli op, on peut être certain que le signal serait écrêté. Un ampli op d'alimentation simple ne peut opérer que sur des signaux dont l'amplitude correspond à son alimentation, et même, on peut s'attendre à une certaine chute de tension d'un ou deux Volts. Donc dans notre cas, les signaux que peut traiter notre ampli op sans les distordre doivent être compris entre 2 et 10 V.
Le diviseur de tension formé par R1, R2 permet de centrer le signal audio autour d'un potentiel de 6V, ce qui rend possible l'opérabilité de l'AOP. La diode Zener D1 joue le rôle de régulateur, elle permet de stabiliser la tension à ses bornes à une valeur voulue en absorbant plus ou moins de courant selon les besoins de la charge, R2 ici. ( voir [1] pour une explication imagée et intuitive.)
L'amplifaction opérationnel permet d'effectuer l'opération de préaccentuation. La norme est celle de la préaccentuation 50µs, qui correspond à une fréquence de 3180 Hz. Le montage de l'amplificateur est celui d'un amplificateur non-inverseur tel que :
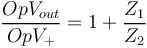
avec
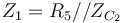
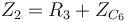
L'objectif de cet étage est d'amplifier uniquement les fréquences supérieures à 3180 Hz.
Ainsi pour cette fréquence de coupure, le signal doit être amplifié de 3dB.
Une analyse par pôles dominants permet de déterminer la fréquence de coupure voulue. Le gain doit être unitaire pour les fréquences inférieurs à 3180 Hz.
En supposant pour les basses fréquences,
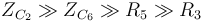
on a :
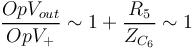
Quand la fréquence augmente, la réactance de C6 diminue de sorte que la relation 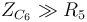 n'est plus valide.
Ainsi la première fréquence de coupure est atteinte lorsque
n'est plus valide.
Ainsi la première fréquence de coupure est atteinte lorsque
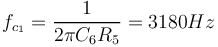
Le gain est à présent fonction de la fréquence avec une pente de 6dB/octave
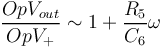
La deuxième contrainte est imposée par la deuxième fréquence de coupure. Elle doit être strictement supérieur à 20kHz ( limite du spectre sonore ) de sorte que le gain soit toujours augmenté jusqu'à cette limite.
Cette deuxième fréquence de coupure est atteinte lorsque la réactance de C6 croise la résistance de R3. Dans ce cas. on obtient :
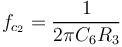
Le gain vaut alors :
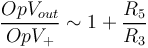
Avec les valeurs de notre schéma, on obtient donc :
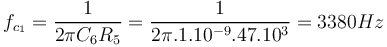
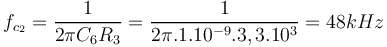
La valeur du condensateur C2 doit être choisie de façon à ce que la relation 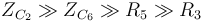 reste valable dans le domaine sonore.
reste valable dans le domaine sonore.
La réponse du système pour ces valeurs est donnée par le graphe ci-dessous.
Section haute fréquence
L'oscillateur que nous utilisons dans cet étage est un VCO LC à transistors couplés en croix ( Cross-coupled LC VCO ) dont la fréquence de résonance dépend de l'inductance L3 et des condensateurs.
Circuit LC
Un circuit LC stocke de l'énergie électrique. Le condensateur stocke de l'énergie dans le champ électrique E entre ses plaques et l'inductance stocke de l'énergie dans son champ magnétique ( qui dépend du courant la traversant.)
Si l'inductance est connectée à un condensateur chargée, le courant commence à traverser la self et celle-ci commence à stocker de l'énergie dans son champ magnétique. Ce faisant, le condensateur commence à se décharger jusqu'à ce que toute la charge soit partie et que la tension à ses bornes atteignent 0. Mais le courant délivré par l'inductance va commencer à charger le condensateur avec un voltage de polarité inverse. L'énergie requise pour charger le condensateur est donc extraite du champ magnétique Quand le champ magnétique est complètement dissipé, le courant stoppe et la charge est de nouveau stockée dans le condensateur, avec une polarité inverse à celle de la condition initiale. Le cycle se répète et la bobine est de nouveau chargée mais le sens du courant est lui aussi inversé.
la fréquence de résonance d'un circuit LC est donné par :
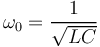
Il est à noter que ni les inductances ni les condensateurs ne sont parfaits, si le circuit n'est pas alimenté par un circuit extérieur, les résistances parasites finiront par dissiper toute l'énergie jusqu'à ce que les oscillations cessent.
Dans notre cas, l'inductance de la résonance est L3 ( ou L4 et L5, ce qui revient au même).
De nombreux éléments capacitifs jouent un rôle dans la résonance. Il y a les capacités C_9, C_ajust, C_11, C_12, les capacités base-collecteur des transistors et les deux varactors D2 et D3.
(Lors de son utilisation, le varactor -ou diode varicap - est polarisée en inverse,
elle fonctionne alors comme un condensateur dont la capacité est ajustable selon la tension négative appliquée sur la diode.)
Cross-coupled VCO
Le VCO que nous utilisons est proche du fonctionnement d'un multivibrateur astable. L'idée est que les deux transistors Q1 et Q2 fonctionnent en commutation de sorte que lorsque l'un des deux est passant, l'autre est bloqué.
Reprenons notre circuit en supprimant les varactors afin de clarifier le montage.
Par rapport au schéma de la figure 7, la fréquence d'oscillation n'est pas seulement donnée par les valeurs des condensateurs et des inductances strictement en parallèle ( L4/L5 et C9 et C_ajust). En effet, les condensateurs reliant les collecteurs et bases des deux transistors influent également ( C11 et C12 ). A ceux-ci il faut ajouter les capacités de jonction base-collecteur des deux transistors qui ne sont pas négligeables dans le calcul des capacités totales.
En effet le modèle réel d'un transistor peut se présenter de la forme suivante :
Dans notre cas, la capacité 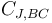 du transistor utilisé (2N3553 adéquat pour les applications d'oscillateurs en VHF) est proche de celle des capacités de base C11 et C12.
Cette capacité dépend de la fréquence de travail et de la voltage collecteur-base.
Dans le modèle SPICE que nous utilisons cette capacité est donnée par le paramètre CJC. Il vaut 34 pF.
du transistor utilisé (2N3553 adéquat pour les applications d'oscillateurs en VHF) est proche de celle des capacités de base C11 et C12.
Cette capacité dépend de la fréquence de travail et de la voltage collecteur-base.
Dans le modèle SPICE que nous utilisons cette capacité est donnée par le paramètre CJC. Il vaut 34 pF.
L'idée est que la charge et décharge de ces capacités vont faire varier la tension Vbe aux bornes des transistors permettant de les faire alterner l'un et l'autre de l'état bloquant à l'état passant.
Supposons que Q2 soit passant et Q1 bloquant. La décharge des condensateurs va conduire à une hausse de tension sur la base de Q1 de sorte que lorsque la tension nécessaire est atteinte ( typiquement 0.6V) le transistor va devenir passant. Le transistor Q1 est alors saturé et ce faisant la tension VCE diminue brutalement pour descendre à 0V ( ou presque ... généralement 0,2V).
Ce brusque changement de tension va ramener les plaques de "gauche" du transistor Q1 à tension très faible inversant donc le champ à leurs bornes. Et comme C12 est relié à la fois au collecteur de Q1 et de la base de Q2, ce brusquement changement va diminuer la tension Vbe de Q2 pour le faire passer en état bloquant et le cycle continue.. Pour un exemple d'un multivibrateur astable fonctionnant avec un circuit RC, voir [2]
La fréquence de résonance de notre système dans ces conditions est donnée par formule suivante tirée de l'article [3]
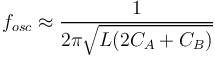
où
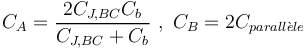
et
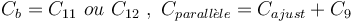
avec les valeurs de la figure 8 et en supposant que la capacité de jonction base-collecteur
vaut 34,6 pF à notre fréquence de travail on a :
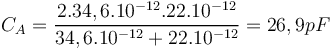
et
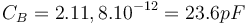
soit:
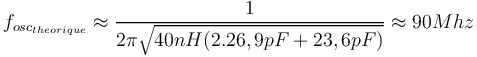
La simulation donne :
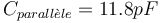
En calculant la période à l'aide des curseurs, on trouve :
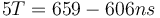
soit
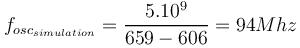
En modifiant la valeur de 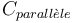 à 36.8 pF on obtient :
à 36.8 pF on obtient :
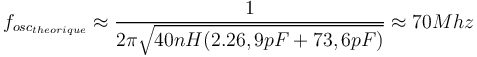
La simulation donne dans ce cas :
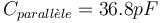
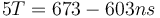
soit
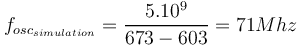
En modifiant les valeurs des condensateurs des jonctions base-collecteurs on peut trouver des fréquences variant de plusieurs Mhz. Il faut donc veiller à lire attentivement les datasheet des transistors pour prévoir les valeurs de ces capacités( on veillera à prendre un transistor de puissance convenable, les puissances mises en jeu étant assez élevées !)
Le système de la figure 8 ne constitue qu'un oscillateur. Si on revient sur la topologie de notre émetteur, on voit apparaître en parallèle des deux condensateurs C_ajust et C_9 les deux varactors D2 et D3. C'est la propriété de ces varicap qui va nous permettre de transformer notre oscillateur en un oscillateur-mélangeur (!). Expliquons.
Le signal préaccentué provenant de la section basse fréquence passe d'abord par la capacité de liaison C3. La résistance R11 permet d'appliquer aux diodes varicap le signal préaccentué. Ainsi le signal pré-accentué va fixer un certain potentiel sur la cathode des deux varactors. Suivant l'amplitude du signal la variation de la capacité des deux diodes sera plus ou moins importante, or ces capacités viennet s'ajouter à ceux de Cajust et C9, la fréquence d'oscillation sera donc modifié.
L'oscillateur fonctionne donc à présent en mélangeur, la résistance R4 permettant de régler l'amplitude du signal appliqué aux bornes de D2 et D3, on règle ainsi l'excursion en fréquence.
Application du signal modulé à l'antenne
La récupération de l'onde modulé se fait par couplage inductif, la seconde self L2, elle-même reliée à l'antenne tout en étant imbriquée dans L3 (voir figure 5), captant le champ électromagnétique émis par L3 : Les deux selfs constituent une sorte d'auto-transformateur.
Pour réaliser les selfs L3 et L2 qui sont de valeur très faible, on peut utiliser des fils électriques " domestiques " et ce, pour plusieurs raisons :
1. Le nombre d'enroulements est très réduit puisque les inductances sont de très faibles valeurs. On peut donc prendre des "gros fils".
2. L'isolation des fils va permettre d'enrouler un fil à l'autre afin de réaliser le couplage magnétique
3. On limite les pertes ohmiques des inductances ( rappelons-le , la résistance d'un fil est donnée par : 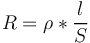 donc plus la section est important plus les pertes dans le fil sont minimisées).
donc plus la section est important plus les pertes dans le fil sont minimisées).
Le risque est que la longueur du fil ne fasse office d'antenne et que des ondes parasites soient captées ça et là.
Pour les selfs que nous allons réaliser, à air et à une seule couche, la formule la plus connue et la plus précise est celle dite de Nagaoka [4].
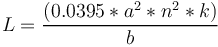
où
a : rayon de la bobine en cm.
b : longueur de la bobine en cm
n : nombre de spires
L : inductance en µH
k : coefficient donné par la relation 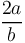
En prenant un enroulement de 5 spires, une longueur totale de 3 cm, un rayon de 0,4 cm on obtient :
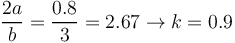
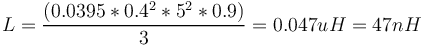
Il est à noter toutefois que cette valeur est donnée avec une approximation de 20% sans compter les approximations lors du montage. C'est pourquoi le condensateur C_ajust de la figure 5 est un condensateur variable : il permettra de fixer la fréquence central de la porteuse. Cependant, ces condensateurs n'ont pas une plage de variation infinie, c'est pourquoi il est important de bien dimensionner la bobine.
Pour la réalisation pratique, on peut utiliser un foret de 3mm de rayon et du fil de cuivre de 1.5 ou 2 mm². La gaine fait un peu moins d'un millimètre d'épaisseur ce qui réduira un peu la valeur de l'inductance.. On enroule d'abord L3 puis on vient intercaler L2 entre les enroulements de L3. Il faut ensuite faire une petite entaille au milieu L3 que l'on reliera à Vcc ( d'où la modélisation de L3 à l'aide de deux inductances L4 et L5 )
fig 12. auto-transformateur "maison"
On pourrait ensuite caractériser cet auto-transformateur "maison" mais on peut être déjà assuré que le rendement ne sera pas de 1!
Simulation système complet
La simulation du système complet a été effectué sous Mixed Sim à l'aide d'Altium. Pour cette simulation nous avons considéré d'une part que les inductances avaient une valeur un peu inférieur à celles que nous avons calculé et avons considéré que l'auto-transformateur n'était pas parfait ( inductance de fuite assez importante ).
La simulation a été réalisé avec les modèles SPICE des transistors 2N3553, avec une inductance L3 valant 30 nH, L2 valant 30 nH, un coefficient de couplage entre les inductances de 0,7, et une valeur de C_ajust de 30 pF.
Le signal qui attaque l'antenne a donc une amplitude de 30V et une fréquence de 89Mhz. La valeur de C_ajust est volontairement fixé à 30 pF puisque nous savons que sa valeur peut varier entre 5pF et 30pF. Si on diminue la valeur de C_ajust, on augmentera la fréquence de la porteuse. Donc a priori notre signal modulé se situera bien dans la bande FM avec comme minimum une fréquence de 88Mhz.
Semaine 3
Oscillateur de réception
Conditions d'oscillation
Le schéma fonctionnel ci-dessous présente la structure générale d'un oscillateur.
La structure d’un oscillateur peut se ramener à celle d’un système bouclé (ou en boucle fermée) constitué par:
-Une chaîne directe ou d’action de fonction de transfert A(p).
-Une chaîne de retour ou de réaction de transmittance B(p).
-Un comparateur qui réalise la différence entre le signal d’entré et la partie du signal de sortie réinjectée à l’entrée.
La fonction de transfert d'un tel système s'écrit :
![T(p) = \frac{V_s(p)}{V_e(p)}=\frac{A(p)}{1+A(p)B(p)}\Rightarrow A(p)V_e(p) = [1+A(p)B(p)]V_s(p)](/mediawiki/images/math/3/2/5/325a08914e3df69326d1b087529c7898.png)
Lorsque le signal d'entrée Ve(t) est nul, on a alors:
![[1+A(p)B(p)]V_s(p) = 0](/mediawiki/images/math/e/7/1/e71ba262e6f6805ca68885f48e17acf9.png) et pour que
et pour que 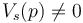 , il faut que :
, il faut que :
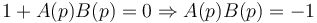 d'où le critère de Barkhausen ou condition d'auto-oscillation
d'où le critère de Barkhausen ou condition d'auto-oscillation
![A(j\omega)B(j\omega) = -1 \Rightarrow
\begin{cases}
Re[A(j\omega)B(j\omega)]\, = -1 \quad \Leftrightarrow \ \ ||A(j\omega)B(j\omega)||= 1\\
Im[A(j\omega)B(j\omega)] = 0 \quad \qquad \quad Arg[A(j\omega)B(j\omega)] = \pi +2k\pi
\end{cases}](/mediawiki/images/math/8/4/b/84bb4abfd502438361e4a114a82fbd4f.png)
|
Dans la pratique, la condition d'accrochage de l'oscillateur est obtenue lorsque 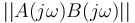 est légèrement supérieur à 1. L'amplitude est ensuite limité par la saturation des composants de sorte que les oscillations ne divergent pas.
est légèrement supérieur à 1. L'amplitude est ensuite limité par la saturation des composants de sorte que les oscillations ne divergent pas.
Topologie
Ci-dessous figure la topologie d'un oscillateur de Clapp dont les paramètres ont été choisi de telle sorte que la tension de commande permette de couvrir l'ensemble de la bande FM.
Le montage ci-dessus est celui-ci d'un collecteur commun (!). En effet le potentiel de référence pour la polarisation correspond bien au potentiel entre R3 et R5, les résistances R4 et R5 abaissant simplement la tension issue de V_pol.( J'ai quelque peu modifié le schéma d'origine, les résistances R4 et R5 servent peut-être seulement de diviseur de tension de sorte que la polarisation soit particulièrement précise, ou alors le concepteur initiale n'avait qu'une alimentation de 9 Volts sous la main... ).
L'émetteur est ici relié à la charge à piloter mais on peut aussi récupérer le signal sur le collecteur, les simulations sont concluantes dans les deux cas.
L'étage d'amplification est réalisé à partir d'un transistor bipolaire, ici de type 2n3904 et d'un circuit de type LC constitué par l'inductance L1, les capacités C2 C3 et celle du varactor.
La capacité de liaison C_L1 empêche la tension de commande ( continue ) de venir perturber la polarisation du transistor. Elle est en série avec la varicap et de valeur beaucoup plus grande que celle de D1. C'est pourquoi sa contribution ne sera pas prise en compte dans les calculs à venir.
La conception du circuit doit prendre en compte certains paramètres de façon à limiter au maximum le bruit de phase de l'oscillateur et ainsi améliorer la pureté spectrale du signal :
1.Transistor doit présenter un faible bruit
2.Q du circuit LC doit être le plus grand possible ( celui-ci détermine la sélectivité du circuit LC : plus il est grand plus les variation de fréquence seront faibles )
3.Les amplitudes des oscillations doivent être assez élevées, elles doivent toutefois restées nettement inférieures à la tension de commande qu'on applique à la diode, C'est pourquoi on utilise souvent des diodes de plusieurs dizaines de Volt de façon à limiter les fluctuations de la capacité de la diode
D'autre part, un paramètre primordial dans la conception du VCO consiste en la calibration du circuit LC de façon à déterminer la bande couverte : le couplage du varactor au circuit LC doit être réalisé de sorte que le VCO délivre toutes les fréquences que nous souhaitons entre F_max et F_min.
Caractérisation de l'oscillateur Clapp
L'objectif de cette partie est de déterminer les conditions et la fréquence d'oscillation.
L'exemple est donné dans le schéma suivant avec un FET, on considère bien sûr qu'il s'agit d'un bjt ( pour les calculs, g11, l'admittance d'entrée du transistor n'est pas nulle avec un bipolaire ). En gras le circuit source (émetteur) du transistor.
le schéma équivalent du transistor correspond à la chaîne d'action et celle du bas au circuit de réaction. Les deux quadripôles sont montés en parallèle de sorte que les matrices d'admittance des deux quadripôles peuvent d'additionner pour former le système global. Et le système oscille à condition que le déterminant de cette matrice soit nul. Expliquons ce dernier point.
Si on reprend le schéma en bloc de la figure 13, on peut remarquer que les courants d’entrée et de sortie de celui-ci doivent être nuls : en effet le montage est autonome (au sens des petits signaux) et ne reçoit donc pas de signal en entrée, ni n’en fournit en sortie.
C'est-à-dire, en notant Y la matrice du système global, Ya la matrice du quadripôle du transistor et Yb celle du quadripôle du circuit LC :
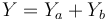
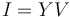
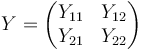
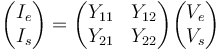
avec,
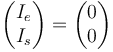 on obtient,
on obtient,
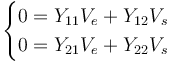
Ce qui conduit à
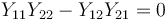
C'est-à-dire à
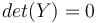
Un article très détaillé donnes tous les développements des calculs ( assez lourds ) menant aux résultats suivants. Il est disponible à l'adresse [5] (se référer aux pages 100-104).
avec les notations de la topologie de la figure 14, on définit :
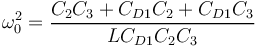
en régime permanent, la fréquence d'oscillation est donnée par :
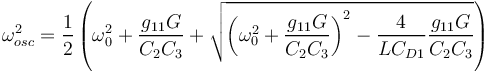
avec g11 l'admittance d'entrée du transistor et 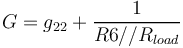 (g22 étant l'admittance de sortie du transistor)
(g22 étant l'admittance de sortie du transistor)
Et pour de grandes valeurs de C2 et C3, on a :
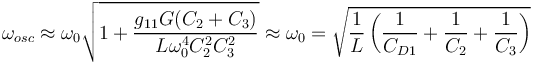
En notant s la transconductance du transistor ( ou la pente du transistor en régime dynamique)
La condition d'oscillation est donnée par :
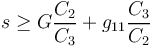
la transconductance s est fonction du courant de collecteur Ic, on peut donc chercher à minimiser la puissance consommée en diminuant le courant de collecteur en considérant s comme une fonction de C2 et C3 et en cherchant
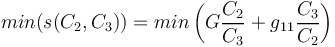
ce qui conduit à
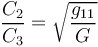
ie
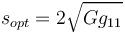
Le rapport entre C2 et C3 est donc primordial dans un tel montage, il faut tacher de les équilibrer tout en veillant à ce que ces deux capacités soient très grandes devant Cd1.
Modèle pour le varactor
Encore une fois, l'oscillateur Clapp que nous utilisons pour réaliser notre oscillateur utilise un varactor ( varicap ) dont la capacité varie en fonction de la tension inverse appliquée à ses bornes. Le modèle de varactor que nous recherchons doit avoir le ratio C_max/C_min le plus élevé possible. D'après l'équation de la fréquence d'oscillation et en supposant que les condensateurs formant le diviseur capacitif soient grands devant la valeur du condensateur de la diode, on pourra obtenir une plus grande plage de fréquence en choisissant un varactor dont le ratio est grand. D'autre part, la plage de tension sous laquelle le varactor peut opérer est à prendre en considération. Par exemple les varactors de la série BBYXX ont des capacités variables pour des valeurs de tension de 0 à 30 Volts. Dans notre cas, avec une alimentation de 12V il vaut mieux utiliser un varactor fonctionnant sous 0/12 Volts pour éviter de rajouter un élévateur de tension au montage.
Nous avons pris le modèle SMV1493. Pour simuler convenablement un tel composant il faut créer son modèle SPICE. Référons-nous d'abord au circuit équivalent du varactor.
Le modèle SMV1493 comprend une inductance Ls de 1,7 nH, une résistance Rs maximale de 0,5 ohms ( grandeur variant avec la fréquence ) et la capacité Cp du boîtier (négligeable ici).
La caractéristique approchée de la capacité de jonction est donnée par la relation :
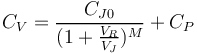
où
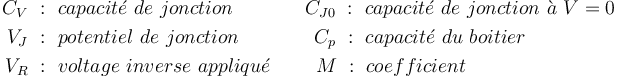
Avec notre modèle, les paramètres sont les suivants :
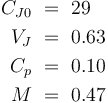
Les tests empiriques fournis par la fiche technique et le tracé de la caractéristique approchée sont relativement proche pour considérer le modèle comme bon.
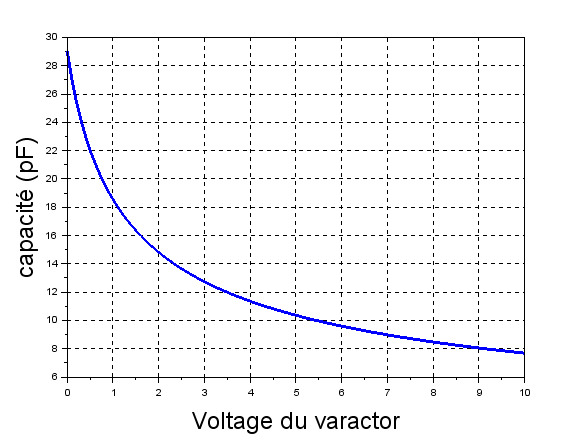
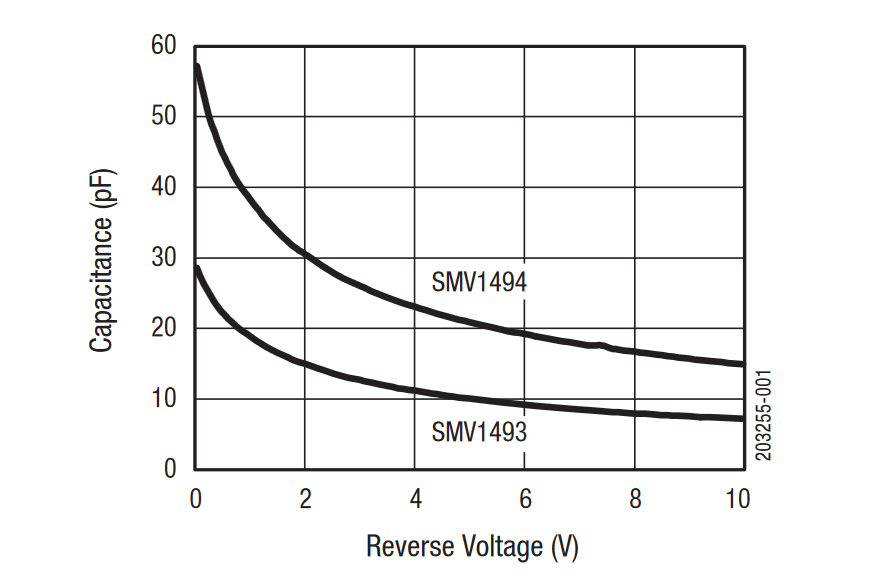
Simulation
Le modèle Spice réalisé pour le SMV1493 est donc
.MODEL SMV1493 D (IS=1E-14 N=1 RS=0.5 XTI=3 EG=1.11 CJO=29E-12 M=0.47
+ VJ=0.63 FC=.5 BV=45.12 IBV=.1232 TT=0)
Les simulations ont été réalisées en ajoutant en parallèle avec le varactor un condensateur C_commande de valeur 6.8pF de façon à stabiliser la valeur de la capacité totale ( autrement les variation de la tension RF aux bornes du varactor induisent des variations de capacité importantes et par conséquent de fréquence d'oscillations. )
Pour la simulation les valeurs de certains composants ont été modifiés par rapport au schéma de la figure 14. C2 vaut 180 pF, C3 vaut 100pF et L 150nH.
En faisant varier la tension de commande sur le varactor, on obtient:
78Mhz pour V_commande = 0V
111Mhz pour V_commande = 10V
Il est toutefois à noter qu'avec un tel système, les plus basses fréquences sont plus sensibles aux variations de fréquences que les plus grandes. En effet
les variations de la valeur de capacité du varactor sont plus intenses pour des tensions faibles, quand on approche de la tension maximale 10V, les variations sont beaucoup plus faibles et n'influent plus
beaucoup sur la capacité. On pourra également utiliser un condensateur variable pour C2 et C3 lors de la réalisation de façon à régler manuellement et à affiner les fréquences désirées.
Filtre d'accord de réception
Le rôle de cette fonction électronique est de sélectionner la fréquence reçue sur l'antenne. En effet si nous ne filtrons pas l'ensemble des signaux que reçoit l'antenne nous pouvons faire face aux problème de la fréquence image lors de la démodulation. Supposons que nous souhaitons démoduler un signal dont la porteuse a une fréquence de f1=80Mhz vers une fréquence intermédiaire de fi=10Mhz. Imaginons que l'antenne reçoit également un signal à la fréquence f2=100Mhz. Dans ce le mélangeur opérera la démodulation sur les deux signaux. Notre fréquence intermédiaire sera donc composée d'un mélange deux signaux portées par les fréquences f1 et f2 ! ( et nous ne voulons pas ça ...)
Pour pallier le problème, il suffit de sélectionner avant d'effectuer la démodulation la fréquence désirée.
Pour cela on utilise un filtre d'accord qui sera reliée à la fréquence de l'oscillateur local.
La difficulté dans la conception de ce filtre est qu'il doit suivre exactement les mêmes variations que l'oscillateur local que nous avons réalisé ( oscillateur de Clapp vu précédemment ). On rappelle qu'en première approximation, la fréquence d'oscillation de l'oscillateur de Clapp est donnée par :
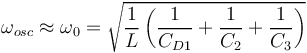
Il faudra donc utiliser une structure similaire à celle que nous avons utilisé pour faire l'oscillateur.
Topologie du filtre d'accord
Semaine 4
démodulateur de fréquence à quadrature
Ce démodulateur permet de mélanger deux signaux de fréquence identique mais de phase différente. Celui-ci permet d'extraire le signal audio du signal de fréquence intermédiaire issu de la première démodulation. Cette fonction électronique s'appuie sur un filtre déphaseur qui permet de modifier la phase du signal d'entrée V.
Mise en équation
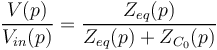
avec
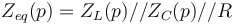
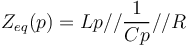
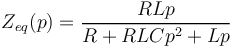
soit
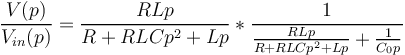
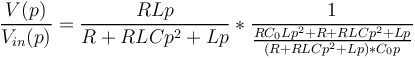
en simplifiant,
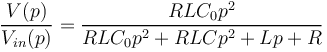
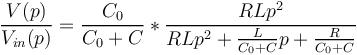
ie,
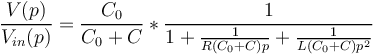
En posant:
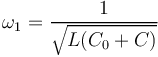
et
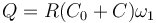
on obtient :
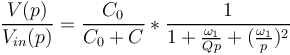
On cherche maintenant à déterminer le déphasage entre nos deux signaux, ce qui revient à calculer l'argument de notre fonction de transfert:
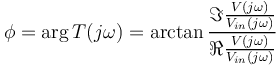
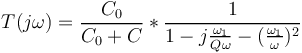
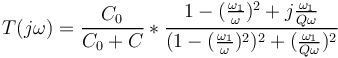
On obtient donc :
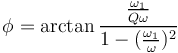
Le graphe de l'argument de la fonction de transfert du filtre est donné pour différentes valeurs de Q, le facteur de qualité.
On constate qu'au voisinage de 1 ( c'est-à-dire quand 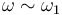 ), le déphasage est d'environ
), le déphasage est d'environ 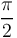 et que la réponse du filtre est proche d'une pente d'équation :
et que la réponse du filtre est proche d'une pente d'équation :
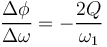
En effet, la dérivée de la réponse est telle que :
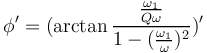
Puisque,
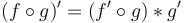
On obtient :
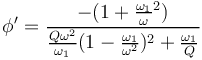
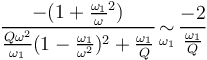
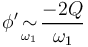
Ainsi, le déphasage total de 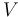 par rapport à
par rapport à 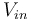 sera de :
sera de :
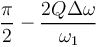
En supposant que 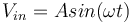 , on a :
, on a :
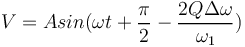
En multipliant les deux signaux, on a :
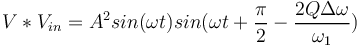
soit en utilisant les fameuses formules de trigonométrie :
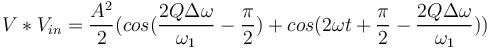
et en filtrant la composante de plus haute fréquence, on obtient :
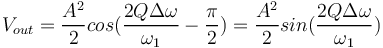
En supposant que 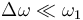 , on obtient :
, on obtient :
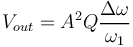
On rappelle que 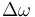 est l'excursion en fréquence du signal dans laquelle on retrouve l'information de notre signal modulé.
La valeur du facteur de qualité doit faire l'objet d'une certaine attention. En effet si on choisit un Q trop élevé, la réponse du filtre pour
est l'excursion en fréquence du signal dans laquelle on retrouve l'information de notre signal modulé.
La valeur du facteur de qualité doit faire l'objet d'une certaine attention. En effet si on choisit un Q trop élevé, la réponse du filtre pour 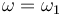 n'est plus linéaire.
Cependant, si on choisit une valeur de Q trop faible, l'amplitude du signal discriminé est trop faible ( voir la dernière équation ).
Puisque la variation de fréquence en bande FM est limité de part et d'autre de la porteuse à 75kHz, avec un filtre centré à 10,7Mhz, on a donc
comme valeur de pulsation normalisée maximale:
n'est plus linéaire.
Cependant, si on choisit une valeur de Q trop faible, l'amplitude du signal discriminé est trop faible ( voir la dernière équation ).
Puisque la variation de fréquence en bande FM est limité de part et d'autre de la porteuse à 75kHz, avec un filtre centré à 10,7Mhz, on a donc
comme valeur de pulsation normalisée maximale:
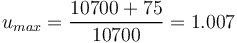
et minimale:
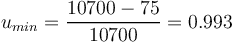
A l'aide de la figure !!!, on détermine graphiquement qu'une valeur de Q comprise entre 20 et 40 convient.
On choisira une valeur Q = 30 pour notre système.
Il faut maintenant dimensionner à partir des équations du circuit, les valeurs des composants du filtre.
Dimensionnement
La fonction électronique décrite ci-dessus est assurée par le SA614.
On sait d'ores et déjà, d'après la fiche technique que la valeur recommandée de la capacité en série 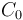 est de 1pF.
D'autre part, la résistance R est interne au SA614 et vaut 40kOhm.
Comme nous avons choisi Q = 30 ( valeur intermédiaire pour éviter la distorsion et pas trop amortir le signal à démoduler) et que
est de 1pF.
D'autre part, la résistance R est interne au SA614 et vaut 40kOhm.
Comme nous avons choisi Q = 30 ( valeur intermédiaire pour éviter la distorsion et pas trop amortir le signal à démoduler) et que 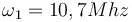 , on détermine la valeur de la capacité C.
, on détermine la valeur de la capacité C.
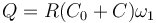
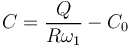
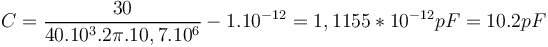
On pourra prendre un condensateur normalisé de la série E48. La valeur la plus proche est de 10pF. ( plus cher mais plus précis ... !)
On en déduit ensuite la valeur de L:
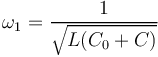
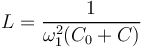
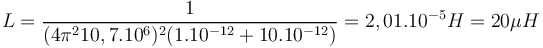
Une simulation du filtre avec les valeurs ci-dessus est donnée ci-dessous.
Le filtre pourrait être un peu mieux centré en ajustant la valeur de l'inductance par exemple ( ce qui est souvent fait en pratique grâce à une inductance variable ). Mais on retrouve bien le déphasage de 90 degrés et la bande passante centrée en 10.7Mhz.
Schémas des systèmes. Explication détaillée des différents points délicats de certains étages du circuit ( cf accord filtre:oscillateur et le bloc pour le détecteur à quadrature) Filtre LC : expliquer le principe. Filtre Céramique: idem. ampli : préaccentuation. Fonctionnement de l'oscillateur de Clapp coté récepteur, Fonctionnement de l'oscillateur côté émetteur : signal modulant dont l'amplitude joue sur le varactor, en conséquence la fréquence du signal oscillant va être légèrement modifié... Système robuste ? à vérifier héhé discussion sur les filtres d'entrée : risque pour ajuster et correctement accordé le circuit de réception.
Choix des composants, risque sur la tolérance ( système performant malgré la tolérance, parfois 20 % ! Partiellement compensé par les condensateurs ajustables.)
Simulation Spice émetteur Schéma, peut être dupliqué... Justification du TL081 : Petit tour de passe-passe permettant de redresser le signal audio dans le positif pour que l'ampli OP puisse travailler correctement ( car l'alimentation est simple ). Voir schéma. Problème : offset de l'ampli OP .... ne délivre pas de tension en dessous de 1.5 V !!! Autre solution : analyse statique de la topologie... En modifiant la valeur de R2, on modifie la tension continue d'entrée de l'oscillateur. EN considérant que l'impédance du TL081 est infinie, on obtient que la tension au point OpV+ vaut U=R1/(R1+R2+R3)*Vcc... EN modifiant la valeur de R2 on obtient un signal gravitant autour de 6V... !
(modèle Spice proche de la réalité ... !!)
Attention à bien charger les modèles SPICE de TOUS les composants à utiliser dans le circuit. L'antenne dont le modèle SPICE était inexistant empêchait
l'algorithme de converger et de donner l'analyse fréquentiel du système, solution : remplacer l'antenne par une charge de 50 ohms.
Modèle Spice pour les varactors à revoir... Impossible de faire osciller le système !!
Revoir éventuellement le couplage inductif dans le modèle ( penser à la directive K Li Lj Lk coeff).
Transistor bloquant passant à revoir également, leur condition de "bascule" cad le switch entre état passant et bloquant n'est pas remplie... à creuser ... )
OUI ! Modèle Spice des transistors 2n2219 qui n'était pas disponible, cette fois ça marche, les petites bascules fonctionnent parfaitement... ! Il y a aussi ce petit problème avec les inducteurs qui ne jouaient pas leur rôle de transformateur... Couplage des signaux sur les collecteurs des deux transistors qui a été possible grâce à ce nouveau modèle... Bien sûr il faudra l'enlever pour réaliser le PCB! Mais la simulaton est néanmoins concluante.
Semaine 5
F=116 Mhz pour la configuration du schéma ... C_ajust = 20pF, inducteurs valant chacun 20 nH, On pourra augmenterla valeur de C_ajust ( notre capa ajustable vaut entre 5 et 30pF) pour mieux se placer dans la bande FM.
Par le calcul, la fréquence de résonance du circuit LC de l'oscillateur est de 115 Mhz...
On rappelle la formule F = 1/2pisqrt(LC_tot).
avec C_tot = C_9 // C_ajust // C_11
C_ajust = 20 pF
C_9 = 6.8pF
C_11= 22pF
L = 40nH
on obtient F_res = 1/2pisqrt(L*C_tot) = 115Mhz.
édition PCB, ne pas oublier qu'on peut cacher des fils dans l'éditeur.. très utile pour éviter de se perdre entre les fils de masses
et les autres... !
Commentaires sur le PCB : quelques largeurs de pistes non négligeables ... Peuvent se comporter comme des antennes : faire un zoom entre R9 et Q2.
Utilisation de composants traversants " contre-nature" en haute fréquence : les liaisons sont plus longues, les résistances et inductances parasites du ciruit sont plus importantes. Mais il est plus facile d'échanger des composants ( condensateur ou self pour le circuit LC résonnant par exemple. )
Problème : antenne un peu trop proche du VCO : risque de perturbation du circuit oscillant. L4 et L3 doivent être voisines sur le PCB : on doit assurer leur couplage magnétique ( on enroule les deux selfs ensembles )
POur le montage de ces selfs : utilisation de petits picots pour pouvoir les monter directement sur le circuit imprimé.
D'abord on bobine L3 ( 5 spires) puis on enroule L4 (4 spires) dans L3. On fait une petite entaille au milieu de L3 pour pouvoir relier le milieu à Vcc. L'inductance d'une bobine est donnée par plusieurs paramètres: le nombre de spires, le diamètre, la hauteur. Une fois le circuit réalisé, on peut éventuellement desserrer ou resserrer les spires pour ajuster la valeur de l'inductance. Mais on ne peut pas augmenter/diminuer le nombre de spires et le diamètre des selfs. L'ajustement du circuit résonnant est donc réaliser à partir d'une capacité variable, qui permettra de choisir la fréquence d'oscillation.