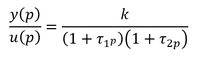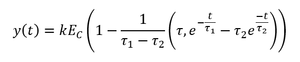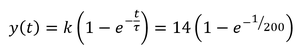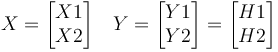IMA4 2017/2018 P60 : Différence entre versions
(→Principes des éléments du système) |
|||
| (111 révisions intermédiaires par 2 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
| + | <include nopre noesc src="/home/pedago/pimasc/include/video-ObservateurCuves-iframe.html" /> | ||
__TOC__ | __TOC__ | ||
<br style="clear: both;"/> | <br style="clear: both;"/> | ||
| Ligne 9 : | Ligne 10 : | ||
[[File:Observateur.png||right|300px]] | [[File:Observateur.png||right|300px]] | ||
| − | Le principal objectif de ce projet est de créer un observateur, c’est-à-dire reconstruire des valeurs dont on ne dispose pas directement (débit de sortie, niveau d’eau, débit dans le tube reliant les 2 cuves) et de | + | Le principal objectif de ce projet est de créer un observateur, c’est-à-dire reconstruire des valeurs dont on ne dispose pas directement (débit de sortie, niveau d’eau, débit dans le tube reliant les 2 cuves) à partir de valeurs mesurées et de celles dont on dispose, provenant du modèle du système qui sera identifié. |
Cet observateur va nous permettre de détecter s’il y a des anomalies (exemple : fuites) dans le système lors d’une simulation grâce à un capteur logiciel. Avec celui-ci nous allons pouvoir d’ailleurs voir la différence des valeurs entre le capteur physique et le capteur logiciel obtenu par l’observateur pour savoir si cela est cohérent. Et pouvoir alors gérer les pannes de capteurs s'il y en a. | Cet observateur va nous permettre de détecter s’il y a des anomalies (exemple : fuites) dans le système lors d’une simulation grâce à un capteur logiciel. Avec celui-ci nous allons pouvoir d’ailleurs voir la différence des valeurs entre le capteur physique et le capteur logiciel obtenu par l’observateur pour savoir si cela est cohérent. Et pouvoir alors gérer les pannes de capteurs s'il y en a. | ||
| Ligne 16 : | Ligne 17 : | ||
==Positionnement par rapport à l'existant== | ==Positionnement par rapport à l'existant== | ||
| − | La mesure d'eau est essentielle pour la collecte de données statistiques et | + | La mesure d'eau est essentielle pour la collecte de données statistiques et la commande de processus de l'industrie chimique, pétrochimique, et nombreux autres secteurs. |
| − | Nous analyserons deux concurrents de différents secteurs. Le premier, ERM automatisme industriels, est chargé de la distribution d'eau | + | Nous analyserons deux concurrents de différents secteurs. Le premier, ERM automatisme industriels, est chargé de la distribution d'eau potable, ils utilisent aussi une système de distribution à base de réservoirs, une pompe et de vannes. |
| − | + | Ils utilisent aussi le programme Labview pour la commande et mesures des réservoirs. Ils font des études des systèmes stables et instables en boucle ouverte ou fermée. Nous analyserons juste un système en boucle fermée. | |
==Analyse du premier concurrent : ERM automatisme industriels== | ==Analyse du premier concurrent : ERM automatisme industriels== | ||
| Ligne 28 : | Ligne 29 : | ||
; Systeme: | ; Systeme: | ||
| − | Son système doit permettre la distribution d'eau potable en quantité suffisante pour satisfaire | + | Son système doit permettre la distribution d'eau potable en quantité suffisante pour satisfaire les besoins quotidiens des usagers et en même temps répondre à des cas |
| − | exceptionnels et urgents (lutter contre les incendies. Le niveau des réservoirs, le débit et la pression de l'eau sont par conséquent contrôlés, ajustés et optimisés en permanence. | + | exceptionnels et/ou urgents (lutter contre les incendies). Le niveau des réservoirs, le débit et la pression de l'eau sont par conséquent contrôlés, ajustés et optimisés en permanence. |
Régulation et distribution d’eau potable: | Régulation et distribution d’eau potable: | ||
Le système est constitué dans sa version de base de: | Le système est constitué dans sa version de base de: | ||
| − | + | ||
| − | + | • Réservoir d’eau représentant une réserve d’eau naturelle | |
| − | + | ||
| − | + | • Cuve de stockage d'eau potable | |
| − | + | ||
| − | + | • Transmetteur de niveau analogique (Ultrasons) pour mesure du niveau d'eau dans la cuve | |
| − | + | ||
| + | • Pompe à débit variable assurant le remplissage de la cuve | ||
| + | |||
| + | • Un Transmetteur de débit analogique (Effet Vortex) | ||
| + | |||
| + | • Vanne ¼ de tour manuelle permettant de régler le débit d'eau gravitaire en sortie de la cuve | ||
| + | |||
| + | • Electrovanne de perturbation de débit | ||
; Commande: | ; Commande: | ||
| Ligne 46 : | Ligne 54 : | ||
• Analyse fonctionnelle: systèmes de stockage et distribution d’eau potable (SysML fourni) | • Analyse fonctionnelle: systèmes de stockage et distribution d’eau potable (SysML fourni) | ||
| + | |||
• Etude des différents principes de mesures (Lois physiques, capteur, transmetteur,...) | • Etude des différents principes de mesures (Lois physiques, capteur, transmetteur,...) | ||
| + | |||
• Etude des pompes à débit variable et des vannes | • Etude des pompes à débit variable et des vannes | ||
| + | |||
• Identification d’un système stable en BO, en BF (Description des différentes méthodes) | • Identification d’un système stable en BO, en BF (Description des différentes méthodes) | ||
| + | |||
• Régulation et asservissement de niveau simple (P, PI, PD, PID), | • Régulation et asservissement de niveau simple (P, PI, PD, PID), | ||
| + | |||
• Régulation de niveau intégrateur | • Régulation de niveau intégrateur | ||
| + | |||
• Etude d’un système instable en BO, en BF(Description des différentes méthodes) | • Etude d’un système instable en BO, en BF(Description des différentes méthodes) | ||
| + | |||
• Etude des économies d’énergie dans la gestion d’un réseau d’eau potable | • Etude des économies d’énergie dans la gestion d’un réseau d’eau potable | ||
| Ligne 62 : | Ligne 77 : | ||
; Problème: | ; Problème: | ||
| − | La régulation du niveau d’eau | + | La régulation du niveau d’eau des piscines. Soit ils n’avaient pas pensé, à la construction, à équiper leur bassin d’un système automatique, soit ce système était tombé en panne et ne pouvait être réparé qu’à grands frais. Les solutions qu’ils avaient trouvé n’étaient pas satisfaisantes : jeter un tuyau d’arrosage dans le bassin et attendre de longues minutes, ou faire « biper » une alarme (mais elle ne bipe jamais au bon moment). |
Bien pratique, ce dispositif peut toutefois, si l’on n’y prend pas garde et s’il n’est pas équipé d’un dispositif d’alerte détectant un remplissage constant et anormal, masquer une éventuelle fuite. Pièce maîtresse, le robinet flotteur est relié généralement directement au réseau d’eau de la commune avec une simple vanne d’isolement, quand elle existe. | Bien pratique, ce dispositif peut toutefois, si l’on n’y prend pas garde et s’il n’est pas équipé d’un dispositif d’alerte détectant un remplissage constant et anormal, masquer une éventuelle fuite. Pièce maîtresse, le robinet flotteur est relié généralement directement au réseau d’eau de la commune avec une simple vanne d’isolement, quand elle existe. | ||
| Ligne 86 : | Ligne 101 : | ||
Ce projet peut être mis en place dans les usines utilisant des fluides comme le pétrole, ou encore du liquide explosif. Ce qui peut représenter un grand danger notamment s'il y a des anomalies dans le processus. | Ce projet peut être mis en place dans les usines utilisant des fluides comme le pétrole, ou encore du liquide explosif. Ce qui peut représenter un grand danger notamment s'il y a des anomalies dans le processus. | ||
| − | Il y a donc une nécessité de superviser chaque mesure du système | + | Il y a donc une nécessité de superviser chaque mesure du système. |
Mais dans ce cas, que faire lors d'une panne de capteurs ? On va devoir vérifier les cas d’erreurs les plus probables. Pour cela, on va avoir besoin de prévoir la valeur des variables critiques du système et l'associer avec une solution possible selon le problème. | Mais dans ce cas, que faire lors d'une panne de capteurs ? On va devoir vérifier les cas d’erreurs les plus probables. Pour cela, on va avoir besoin de prévoir la valeur des variables critiques du système et l'associer avec une solution possible selon le problème. | ||
| Ligne 104 : | Ligne 119 : | ||
Pour ce projet, nous allons avoir à disposition le système à 2 réservoirs présent en C008. | Pour ce projet, nous allons avoir à disposition le système à 2 réservoirs présent en C008. | ||
| − | Celui est composé de deux réservoirs, six vannes, d'un serpentin de retard, d'une pompe et d'un panneau de commande. Ce système est commandé par un ordinateur équipé d’une carte d’acquisition National Instrument, et du noyau Temps Réel dans le logiciel Matlab. | + | Celui-ci est composé de deux réservoirs, six vannes, d'un serpentin de retard, d'une pompe et d'un panneau de commande. Ce système est commandé par un ordinateur équipé d’une carte d’acquisition National Instrument, et du noyau Temps Réel dans le logiciel Matlab. |
Matlab simulink est un logiciel de modélisation visuelle des systèmes physiques et dynamiques qui peut simuler diverses données avec l'objectif d’assurer que le système marche conformément aux spécifications données et aussi l’optimiser. | Matlab simulink est un logiciel de modélisation visuelle des systèmes physiques et dynamiques qui peut simuler diverses données avec l'objectif d’assurer que le système marche conformément aux spécifications données et aussi l’optimiser. | ||
| Ligne 122 : | Ligne 137 : | ||
Modélisation mathématique du système à l'aide des lois physiques puis estimation des paramètres du modèle à l'aide des données (débit d'entrée et hauteurs mesurées). | Modélisation mathématique du système à l'aide des lois physiques puis estimation des paramètres du modèle à l'aide des données (débit d'entrée et hauteurs mesurées). | ||
| − | <u>''Exemple :''</u> Si on a modélisé le système et on obtient un deuxième ordre qui est de la forme : Y(p) | + | <u>''Exemple :''</u> Si on a modélisé le système et on obtient un deuxième ordre qui est de la forme : |
| + | <math> | ||
| + | \frac{Y(p)}{U(p)} = \frac{K}{p^2+ap+b} | ||
| + | </math> | ||
Pour estimer les paramètres du modèle, il faut estimer K, a et b | Pour estimer les paramètres du modèle, il faut estimer K, a et b | ||
| Ligne 131 : | Ligne 149 : | ||
<u>'''Etape 3 :'''</u> | <u>'''Etape 3 :'''</u> | ||
| − | Génération des signaux indicateurs de défauts appelés résidus à partir des mesures recueillies directement sur le système physique et données générées par l'observateur | + | Génération des signaux indicateurs de défauts appelés résidus à partir des mesures recueillies directement sur le système physique et des données générées par l'observateur |
| − | <u>'''Etape 4 :'''</u> | + | <u>'''Etape 4 (optionnel) :'''</u> |
Mise en place d'un test statistique pour générer des alarmes | Mise en place d'un test statistique pour générer des alarmes | ||
| Ligne 141 : | Ligne 159 : | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | !Tâche !! Prélude !! Heures S1 !! Heures S2 !! Heures S3 !! Heures S4 !! Heures S5 !! Heures S6 !! Heures S7 !! Heures S8 !! Heures S9 !! Heures S10 !! Heures S11 !! Heures S12 !! Heures S13 !! Total | + | !Tâche !! Prélude !! Heures S1 !! Heures S2 !! Heures S3 !! Heures S4 !! Heures S5 !! Heures S6 !! Heures S7 !! Heures S8 !! Heures S9 !! Heures S10 !! Heures S11 !! Heures S12 !! Heures S13 !!Heures supp !! Total |
|- | |- | ||
| Analyse du projet | | Analyse du projet | ||
| 8 | | 8 | ||
| + | | | ||
| | | | ||
| | | | ||
| Ligne 171 : | Ligne 190 : | ||
| 2 | | 2 | ||
| 2 | | 2 | ||
| − | | | + | | 1 |
| − | | | + | | 1 |
| − | | | + | | 1 |
| − | | | + | | 1 |
| − | | | + | | 6 |
| + | | 26 | ||
|- | |- | ||
| Modélisation sous Simulink | | Modélisation sous Simulink | ||
| Ligne 192 : | Ligne 212 : | ||
| | | | ||
| | | | ||
| − | | | + | | 0,5 |
| + | | 8,5 | ||
|- | |- | ||
| Filtrage du signal + Étalonnage des réservoirs (tension -> cm) | | Filtrage du signal + Étalonnage des réservoirs (tension -> cm) | ||
| Ligne 208 : | Ligne 229 : | ||
| | | | ||
| | | | ||
| + | | 2 | ||
| | | | ||
| − | | | + | | 11 |
|- | |- | ||
| Recherche sur les différents éléments du système (principe, datasheet,..) | | Recherche sur les différents éléments du système (principe, datasheet,..) | ||
| Ligne 224 : | Ligne 246 : | ||
| | | | ||
| | | | ||
| + | | | ||
| | | | ||
| | | | ||
| − | | | + | | 13 |
|- | |- | ||
| Simulation sur système réel pour récupérer des données | | Simulation sur système réel pour récupérer des données | ||
| Ligne 239 : | Ligne 262 : | ||
| 2 | | 2 | ||
| 1 | | 1 | ||
| + | | 3 | ||
| + | | 2 | ||
| + | | 2 | ||
| + | | | ||
| | | | ||
| + | | 10 | ||
| + | |- | ||
| + | | Identification du système : Fonction de transfert, modèle d'état | ||
| + | | | ||
| | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | 1 | ||
| + | | 2 | ||
| + | | 2 | ||
| + | | 2 | ||
| + | | | ||
| + | | 7 | ||
| + | |- | ||
| + | | Observateur | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| | | | ||
| | | | ||
| | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | 1 | ||
| + | | 2 | ||
| + | | 3 | ||
|} | |} | ||
| + | |||
| + | ==Présentation générale du système== | ||
| + | |||
| + | [[File:2cuves.png||vignette|right|350px|Schéma du système des 2 cuves]] | ||
| + | |||
| + | |||
| + | Notre système est composé de 2 cuves, dont la première est remplie en eau par le biais d'une pompe, elle-même alimentée par un moteur dont on choisira la tension par la suite. La pompe est reliée à une grosse cuve qui sert en quelque sorte de réservoir afin de récupérer l'eau qui sera ensuite vidée dans ce même réservoir lorsqu'on ouvre les différentes vannes. | ||
| + | |||
| + | Il y a une sortie principale du système : Vanne de sortie. | ||
| + | Le reste des sorties ne simulent que les fuites, comme "Vanne de fuite" et "Fuite cuve". Nous avons également "Fuite pompe", qui génère aussi une fuite. | ||
| + | "Fuite pompe" et "Vanne fuite" sont toutes les deux des électrovannes à contrôler par le tableau de commande, alors que "Vanne de fuite" est une vanne manuelle. Il reste une vanne manuelle, qui relie les 2 cuves ensemble, elle peut être fermée si on ne veut remplir que la première cuve (pour travailler sur un premier ordre) ou ouverte pour remplir les deux cuves. | ||
| + | |||
| + | Le système dispose également de deux capteurs de pression (un dans chaque cuve) permettant d'avoir des données afin de connaître le niveau d'eau de chaque cuve. Ces données seront en volts, il faudra donc trouver un moyen pour avoir un niveau d'eau en cm et non en volts. | ||
==Principes des éléments du système== | ==Principes des éléments du système== | ||
| Ligne 256 : | Ligne 329 : | ||
; MATLAB | ; MATLAB | ||
| − | En utilisant les matériels NI, nous avons en main un système d'exploitation, un environnement de développement d'application et un choix d'applications logicielles souples. On utilise alors le logiciel MATLAB pour développer le système pour les applications de test, de mesure et de contrôle/commande, qui permet d’accéder rapidement au matériel et aux informations sur les données et on peut afficher les signaux d'E/S. Une interface en ligne de commande, qui est un des éléments du bureau MATLAB, nous permet d’exécuter des commandes simples. Des séquences de commandes peuvent être sauvegardés dans un fichier texte, sous la forme d’un « script » ou | + | En utilisant les matériels NI, nous avons en main un système d'exploitation, un environnement de développement d'application et un choix d'applications logicielles souples. On utilise alors le logiciel MATLAB pour développer le système pour les applications de test, de mesure et de contrôle/commande, qui permet d’accéder rapidement au matériel et aux informations sur les données et on peut afficher les signaux d'E/S. Une interface en ligne de commande, qui est un des éléments du bureau MATLAB, nous permet d’exécuter des commandes simples. Des séquences de commandes peuvent être sauvegardés dans un fichier texte, sous la forme d’un « script » ou encapsulées dans une fonction pour obtenir des calculs. |
| + | |||
Par exemple, les calculs du filtre PB : | Par exemple, les calculs du filtre PB : | ||
| Ligne 274 : | Ligne 348 : | ||
- Relier la borne du signal d'entrée du système à l'entrée E1 (ach0) | - Relier la borne du signal d'entrée du système à l'entrée E1 (ach0) | ||
| − | - Relier | + | - Relier l'entrée S au débit que la pompe doit fournir (DAC0) |
Sur le logiciel Matlab les entrées commencent à partir de 1, contrairement au SC-2345 qui commence en 0. Si on veut alors retrouver le numéro de channel attribué aux entrées/sorties, on notera leur numéro +1. Ici, le capteur H1 se trouvera alors en channel 4 et le capteur H2 en channel 10. | Sur le logiciel Matlab les entrées commencent à partir de 1, contrairement au SC-2345 qui commence en 0. Si on veut alors retrouver le numéro de channel attribué aux entrées/sorties, on notera leur numéro +1. Ici, le capteur H1 se trouvera alors en channel 4 et le capteur H2 en channel 10. | ||
| Ligne 286 : | Ligne 360 : | ||
Pour commencer, afin de créer le modèle sous Simulink, il nous fallait savoir comment était contrôlée la '''pompe''' du système pour faire parvenir l'eau jusqu'aux cuves. Après quelques observations, nous constatons que la pompe est commandée par un moteur situé à l'intérieur du système. | Pour commencer, afin de créer le modèle sous Simulink, il nous fallait savoir comment était contrôlée la '''pompe''' du système pour faire parvenir l'eau jusqu'aux cuves. Après quelques observations, nous constatons que la pompe est commandée par un moteur situé à l'intérieur du système. | ||
| − | Pour faire démarrer le moteur, il nous faut donc lui envoyer une certaine tension. Sous Simulink, pour envoyer une tension, nous plaçons un bloc '''step''', qui correspond à un signal | + | Pour faire démarrer le moteur, il nous faut donc lui envoyer une certaine tension. Sous Simulink, pour envoyer une tension, nous plaçons un bloc '''step''', qui correspond à un signal de X Volts que nous avons à définir. Nous avons alors donné une valeur de 5V arbitrairement, qui pourra être modifiée par la suite mais qui pour l'instant est suffisante pour faire tourner le moteur qui déclenche la pompe et nous permet de remplir les cuves d'eau. |
Pour envoyer cette tension au moteur du système on utilise le bloc '''"Analog Output"''' (car c'est une valeur qu'on envoie) en paramétrant le numéro de channel sur 1 car l'entrée de la pompe est câblée sur ACH0 (expliqué dans la partie précédente). La tension est alors envoyée via le boitier SC-2345, ce qui permet d'alimenter le moteur, et donc de démarrer la pompe qui va pouvoir remplir une ou deux cuve(s) avec un certain débit. | Pour envoyer cette tension au moteur du système on utilise le bloc '''"Analog Output"''' (car c'est une valeur qu'on envoie) en paramétrant le numéro de channel sur 1 car l'entrée de la pompe est câblée sur ACH0 (expliqué dans la partie précédente). La tension est alors envoyée via le boitier SC-2345, ce qui permet d'alimenter le moteur, et donc de démarrer la pompe qui va pouvoir remplir une ou deux cuve(s) avec un certain débit. | ||
Ensuite, ce que l'on veut récupérer comme données pour l'instant c'est le niveau d'eau de chaque cuve. | Ensuite, ce que l'on veut récupérer comme données pour l'instant c'est le niveau d'eau de chaque cuve. | ||
| − | Pour récupérer ces valeurs, on regarde où sont | + | Pour récupérer ces valeurs, on regarde où sont câblées les sorties de chacun des capteurs. On note que le capteur pour la première cuve est câblé sur ACH3, et le capteur de la seconde cuve est câblé sur ACH9. On va alors placer 2 blocs '''"Analog Input"''' (car on reçoit des données) sur Simulink, un avec comme numéro de channel 4 (1ère cuve) et un avec un numéro de channel 10 (2ème cuve). |
On place alors dans un premier temps un scope à chaque sortie pour visualiser les signaux de chaque capteur. On remarque alors que nos signaux sont très bruités et qu'ils ont une valeur qui ne correspond pas du tout à une mesure de niveau en cm (ce qui est normal vu qu'on a des capteurs de pression). | On place alors dans un premier temps un scope à chaque sortie pour visualiser les signaux de chaque capteur. On remarque alors que nos signaux sont très bruités et qu'ils ont une valeur qui ne correspond pas du tout à une mesure de niveau en cm (ce qui est normal vu qu'on a des capteurs de pression). | ||
| − | Pour avoir un signal correct à étudier, on va filtrer le signal afin de réduire un maximum le bruit. Pour cela, on va ajouter le bloc '''"Discrete Transfer"''', qui prend en paramètre | + | Pour avoir un signal correct à étudier, on va filtrer le signal afin de réduire un maximum le bruit. Pour cela, on va ajouter le bloc '''"Discrete Transfer"''', qui prend en paramètre les coefficients du numérateur et du dénominateur de la fonction de transfert. La démarche de cette méthode sera expliquée dans une prochaine partie. |
| − | On a désormais un signal filtré mais nous avons toujours des valeurs qui ne correspondent pas à une mesure en cm. Il va falloir, pour résoudre ce problème, étalonner notre signal. On place alors un bloc '''" | + | On a désormais un signal filtré mais nous avons toujours des valeurs qui ne correspondent pas à une mesure en cm. Il va falloir, pour résoudre ce problème, étalonner notre signal. On place alors un bloc '''"Function Block Parameters"''', qui utilise la méthode d'interpolation pour réaliser notre étalonnage. On va alors affecter à chaque 5 cm, la valeur que l'on reçoit du capteur. Ceci sera également expliqué dans la prochaine partie plus en détails. |
On aura alors en sortie de chaque capteurs (après avoir passé chaque bloc) un signal qui correspond au niveau d'eau en cm, de chaque cuve en temps réel. | On aura alors en sortie de chaque capteurs (après avoir passé chaque bloc) un signal qui correspond au niveau d'eau en cm, de chaque cuve en temps réel. | ||
| − | + | Maintenant que ceci est fait, nous avons créé un sous système qui regroupe les blocs de filtrage et d'étalonnage du système afin que cela soit plus épuré dans notre système final. | |
==Filtrage du signal et étalonnage== | ==Filtrage du signal et étalonnage== | ||
[[Fichier:filtre_etalonnage.jpg||vignette|right|300px]] | [[Fichier:filtre_etalonnage.jpg||vignette|right|300px]] | ||
| − | Pour résoudre le problème du bruit sur le signal de sortie, nous avons d'abord | + | Pour résoudre le problème du bruit sur le signal de sortie, nous avons d'abord réglé la fonction de transfert de notre filtre pour diminuer le bruit avec une valeur de gain obtenue à l'aide des fonctions tf et c2d (conversion d'un système de temps continu à temps discret) de MATLAB. |
Nous avons par la suite ajouté l'étalonnage, sa fonction est de donner une relation de valeurs entre la tension reçue et la hauteur en cm du réservoir. Car les capteurs de pression du niveau d’eau mesurent seulement une tension. Ainsi, pour trouver les valeurs à mettre dans notre bloc pour l'étalonnage, une personne a visualisé la hauteur de l'eau tous les 5cm de chaque cuve, tandis que la deuxième a noté les valeurs correspondantes en tension indiquées grâce au scope placé sur notre système Simulink. | Nous avons par la suite ajouté l'étalonnage, sa fonction est de donner une relation de valeurs entre la tension reçue et la hauteur en cm du réservoir. Car les capteurs de pression du niveau d’eau mesurent seulement une tension. Ainsi, pour trouver les valeurs à mettre dans notre bloc pour l'étalonnage, une personne a visualisé la hauteur de l'eau tous les 5cm de chaque cuve, tandis que la deuxième a noté les valeurs correspondantes en tension indiquées grâce au scope placé sur notre système Simulink. | ||
| − | Lors de la phase d'étalonnage, il faut que les vannes restent dans la même position, par conséquent nos résultats étaient faux lors de notre première mesure et nous avons du réitérer cette opération. Car nous avions fait l'étalonnage sur le premier réservoir en fermant la vanne reliant les 2 cuves, puis nous avions ouvert celle ci pour réaliser l'étalonnage sur le second réservoir et de ce fait cela | + | Lors de la phase d'étalonnage, il faut que les vannes restent dans la même position, par conséquent nos résultats étaient faux lors de notre première mesure et nous avons du réitérer cette opération. Car nous avions fait l'étalonnage sur le premier réservoir en fermant la vanne reliant les 2 cuves, puis nous avions ouvert celle ci pour réaliser l'étalonnage sur le second réservoir et de ce fait cela modifiait les résultats obtenus sur le premier réservoir. |
De plus, notre tuteur nous a demandé de recalibrer notre signal d'entrée du système qui correspond à une tension envoyée au moteur qui commande la pompe, en regardant au niveau du signal de sortie sur le scope à partir de quelle tension la courbe devient linéaire, et ensuite ajuster le signal d'entrée en fonction de ceci. | De plus, notre tuteur nous a demandé de recalibrer notre signal d'entrée du système qui correspond à une tension envoyée au moteur qui commande la pompe, en regardant au niveau du signal de sortie sur le scope à partir de quelle tension la courbe devient linéaire, et ensuite ajuster le signal d'entrée en fonction de ceci. | ||
| Ligne 318 : | Ligne 392 : | ||
==Fonction de transfert du système== | ==Fonction de transfert du système== | ||
| − | {{ | + | [[Fichier:5-6-1p.png||vignette|right|300px|Simulation du systéme]] |
| + | |||
| + | En regardant les signaux des deux capteurs de niveau d’eau, avec notre tuteur, nous avons conclu que le système a un comportement non linéaire pour une tension d'entrée à 3 volts. De ce fait, pour la suite du projet, nous allons ignorer cette plage de valeurs (0 à 3V) en entrée. | ||
| + | Le capteur de pression servant pour les niveaux d'eau ne sont pas précis. En effet, si nous augmentons le signal d’entrée entre 0 et 9 volts, le débit de la pompe change et par conséquent, la pression varie et ne donne pas en temps réel le bon résultat. Il y a toujours un laps de temps pour que cela se stabilise un minimum. | ||
| + | |||
| + | Nous identifions alors notre système de deux cuves comme système du deuxième ordre. | ||
| + | Les équations différentielles linéaires de deuxième ordre et de coefficients constants, décrivent la dynamique d’un système qui à l’intérieur a deux éléments de stockage d'énergie, dans notre cas, il s'agit des deux réservoirs d’eau. | ||
| + | Nous avons fait une simulation avec une signal d’entrée de 5 volts pendant 10 minutes et à 6 volts pendant 56 minutes et nous avons obtenu un signal pour chaque cuve de la hauteur par rapport au temps. | ||
| + | |||
| + | On décrira notre système linéaire du second ordre avec le modèle mathématique, il aura une fonction de transfert sous la forme suivante : | ||
| + | |||
| + | [[Fichier:FT1.png||vignette|left|200px|Fonction de transfert en forme canonique]] | ||
| + | [[Fichier:FTt.png||vignette|center|300px|Fonction de transfert par rapport au temps]] | ||
| + | |||
| + | <br> | ||
| + | <br> | ||
| + | Nous avons choisi les valeurs de la fonction, en tenant compte de la courbe de la cuve 1 à 6 volts. Le gain (K) est la différence entre la hauteur maximale et minimale, c'est à dire 35,5-21,5=14. Pour les valeurs des τn nous avons tracé une tangente au point d'inflexion de cette courbe. La tangente à t=0 est horizontale et la tangente au point d'inflexion de la courbe coupe l'axe des abscisses en τ1 et l'asymptote de la valeur finale en τ1+τ2. Le point d'inflexion sera à 63% du le gain (14*0,63=8,82) et τ sera égal au point sur l'intersection de l'axe de temps qui correspond à la hauteur (21,5+8,82). | ||
| + | |||
| + | |||
| + | [[Fichier:tan.png||vignette|center|300px]] | ||
| + | |||
| + | [[Fichier:1ordreserie.png||vignette|right|200px]] | ||
| + | |||
| + | |||
| + | Nous avons mesuré la valeur de τ1 et dans notre cas elle est quasi nulle, donc comme le système est équivalent à deux systèmes du 1er ordre placés en série, il est possible de le simplifier à un système de second ordre. | ||
| + | |||
| + | Finalement la fonction de transfert est: | ||
| + | |||
| + | [[Fichier:FT.png||vignette|center|300px]] | ||
| + | |||
| + | ==Modèle d'état== | ||
| + | |||
| + | En automatique, une représentation d'état permet de modéliser un système dynamique en utilisant des variables d'état. Cette représentation, qui peut être linéaire ou non, continue ou discrète, permet de déterminer l'état du système à n'importe quel instant futur si l'on connaît l'état à l'instant initial et le comportement des variables exogènes qui influent sur le système. La représentation d'état du système permet de connaître son comportement "interne" et pas seulement son comportement "externe" comme c'est le cas avec sa fonction de transfert. | ||
| + | [[File:Representation_etat.jpg||right|300px]] | ||
| + | |||
| + | La représentation d'état de ces systèmes, quand ils sont à temps continu, s'écrit de la manière suivante : | ||
| + | <Center><math>\left\{ | ||
| + | \begin{array}{c} | ||
| + | \dot{x}=A~x+B~u \\ | ||
| + | y=C~x+D~u | ||
| + | \end{array} | ||
| + | \right. </math> </center> | ||
| + | |||
| + | <math> x\left( t\right) \in \mathbb{R}^{n}</math> : colonne qui représente les ''n'' variables d'état<br /> | ||
| + | <math> u\left( t\right) \in \mathbb{R}^{m}</math> : colonne qui représente les ''m'' commandes <br /> | ||
| + | <math> y\left( t\right) \in \mathbb{R}^{p}</math> : colonne qui représente les ''p'' sorties<br /> | ||
| + | |||
| + | |||
| + | <math> A \in \mathbb{R}^{n\times n} </math> : Matrice d'état<br /> | ||
| + | <math> B \in \mathbb{R}^{n\times m} </math> : Matrice de commande<br /> | ||
| + | <math> C \in \mathbb{R}^{p\times n} </math> : Matrice d'observation<br /> | ||
| + | <math> D \in \mathbb{R}^{p\times m} </math> : Matrice d'action directe | ||
| + | |||
| + | Dans notre cas, nous allons faire l'identification entre fonction de transfert et modèle d'état pour trouver A, B, C et D. | ||
| + | |||
| + | On a en théorie pour un système du 1er ordre : | ||
| + | <center><math> \frac{Y(s)}{U(s)} =\frac{k}{1+tau.p} = \frac{\frac{k}{tau}}{p+\frac{1}{tau}} = \frac{b0}{a1.p+a0} </math></center> | ||
| + | |||
| + | Ce qui nous donne dans notre cas, avec nos fonctions de transfert : | ||
| + | |||
| + | <Center><math>\left\{ | ||
| + | \begin{array}{c} | ||
| + | \dot{x1}=\frac{1}{tau}~x1+1~u \\ | ||
| + | y1=\frac{k}{tau}~x1+0~u | ||
| + | \end{array} | ||
| + | \right. | ||
| + | ~~~~ | ||
| + | \left\{ | ||
| + | \begin{array}{c} | ||
| + | \dot{x2}=\frac{1}{tau2}~x2+1~u \\ | ||
| + | y2=\frac{k2}{tau2}~x2+0~u | ||
| + | \end{array} | ||
| + | \right. </math> </center> | ||
| + | |||
| + | Ceci représente 2 modèles que l'on va rassembler en un. | ||
| + | |||
| + | <Center><math>\left\{ | ||
| + | \begin{array}{c} | ||
| + | \dot{x1}=A1~x1+B1~u \\ | ||
| + | y1=C1~x1+D1~u | ||
| + | \end{array} | ||
| + | \right. | ||
| + | ~~~~ | ||
| + | \left\{ | ||
| + | \begin{array}{c} | ||
| + | \dot{x2}=A2~x2+B2~u \\ | ||
| + | y=C2~x2+D2~u | ||
| + | \end{array} | ||
| + | \right. </math> </center> | ||
| + | |||
| + | On pose : | ||
| + | :: <math> | ||
| + | X = \begin{bmatrix} X1 \\ X2 \end{bmatrix} | ||
| + | ~~~ | ||
| + | Y = \begin{bmatrix} Y1 \\ Y2 \end{bmatrix} =\begin{bmatrix} H1 \\ H2 \end{bmatrix} | ||
| + | </math> | ||
| + | |||
| + | On aura alors : | ||
| + | |||
| + | <Center><math> | ||
| + | \dot{X} = \begin{bmatrix} \dot{X1} \\ \dot{X2} \end{bmatrix} | ||
| + | = \begin{bmatrix} A1 & 0 \\ 0 & A2 \end{bmatrix} \begin{bmatrix} X1 \\ X2 \end{bmatrix} | ||
| + | + \begin{bmatrix} B1 \\ B2 \end{bmatrix} u | ||
| + | = A~x+B~u | ||
| + | </math></center> | ||
| + | |||
| + | |||
| + | <Center><math> | ||
| + | Y = \begin{bmatrix} Y1 \\ Y2 \end{bmatrix} | ||
| + | = \begin{bmatrix} C1 & 0 \\ 0 & C2 \end{bmatrix} \begin{bmatrix} X1 \\ X2 \end{bmatrix} | ||
| + | = C~x | ||
| + | </math></center> | ||
| + | |||
| + | On implémente le modèle d'état que l'on vient de trouver dans notre fichier Simulink, dans le sous-système du modèle boîte noire. | ||
| + | |||
| + | ==Observateur== | ||
| + | |||
| + | Si on veut estimer x et y (vu précédemment dans le modèle d'état), on les construit par la sortie, qui elle même a un défaut. | ||
| + | Pour cela, on va utiliser la méthode de l'espace de parité. | ||
| + | |||
| + | On réalise cette méthode à partir des équations présentes dans le modèle d'état, que l'on va dériver n fois (dans la théorie). | ||
| + | |||
| + | ;Théorie de la méthode: | ||
| + | |||
| + | <math> | ||
| + | X = AX + BU | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | Y = CX + DU ~ => ~ | ||
| + | \dot{Y} = C \dot{X} + B \dot{U} = C (AX + BU) + D\dot{U} = CAX + CBU + D\dot{U} | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \begin{align}\ddot{Y} &= CA\dot{X} + CB\dot{U} + D\ddot{U} \\ \ & = CA(AX+BU) + CB\dot{U} + D\ddot{U} | ||
| + | \\ \ &= CA^2X + CABU + CB\dot{U} + D\ddot{U} \\ \ & = CA^2X + \begin{bmatrix} CAB & CB & D \end{bmatrix} \begin{bmatrix} U \\ \dot{U} \\ \ddot{U} \end{bmatrix} \end{align} | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \begin{align}Y^3 &= ... \\ \ &Y^n = ... \end{align} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | Dans notre cas, on a n=1 car on utilise une équation du premier ordre. | ||
| + | |||
| + | Ce qui nous donne : | ||
| + | |||
| + | <math> | ||
| + | \begin{bmatrix} Y \\ \dot{Y} \end{bmatrix} = \begin{bmatrix} C \\ CA \end{bmatrix} X + \begin{bmatrix} D & 0 \\ CB & D \end{bmatrix} \begin{bmatrix} U \\ \dot{U} \end{bmatrix} | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | <=> Y = \gamma X + H U | ||
| + | </math> | ||
| + | |||
| + | |||
| + | On veut trouver une matrice qui annule Γ en la multipliant. | ||
| + | Pour ce faire, nous allons utiliser le théorème de Cayley Hamilton, et nous nommerons la matrice : Γ <sup>t</sup>, matrice orthogonale. | ||
| + | |||
| + | Celle-ci sera créée sur Matlab grâce à la fonction '''null()''' avec Γ' (" ' " pour la transposée) en paramètre. | ||
| + | Cela va nous retourner une matrice contenant des valeurs possibles afin d'annuler la matrice Γ. | ||
| + | |||
| + | Maintenant, l'idée est d'avoir un signal de défaut (que l'on nommera f par la suite) donc en prenant la première ligne de cette matrice on a un vecteur de la base, ce qui est suffisant. | ||
| + | Pour ne récupérer que la première ligne, on procède comme ceci : <math> \Gamma 0=\Gamma ^t<(1,:) </math> | ||
| + | |||
| + | Comme nous avons 2 sorties (H1 et H2), nous allons avoir besoin de 2 défauts. On va, de ce fait récupérer également la deuxième ligne de Γ. | ||
| + | |||
| + | On a alors : | ||
| + | |||
| + | <math> | ||
| + | \gamma ^t \gamma=0 | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \begin{align} \gamma ^t Y= \gamma ^t \gamma X + \gamma ^t HU + f \\ = \gamma ^t HU + \gamma ^t f | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | Donc : | ||
| + | |||
| + | <math> | ||
| + | E = \gamma ^t f = \gamma ^t Y - \gamma ^t HU | ||
| + | </math> | ||
| + | |||
| + | E représentant le '''"résidu"''', soit l'erreur qui peut avoir dans le système, généré par exemple par un ou plusieurs fuites. | ||
| + | Nous pouvons maintenant implémenter ceci sur notre Simulink. | ||
| + | |||
| + | [[File:simulink1.png|center|600px|Simulink]] | ||
| + | |||
| + | On soustrait - 5 lorsque l'on récupère U afin de se placer au point de fonctionnement (de redéfinir l'origine en quelque sorte). Nous devons obligatoirement réaliser cela car nous travaillons sur un système de base non linéaire, donc on va se concentrer uniquement sur une partie linéaire, dont l'origine est à 5V. Et on travaillera dans ce voisinage de valeurs. | ||
| + | |||
| + | Pour mettre en place le résidu, nous utilisons des dérivées. Avec le signal d'entrée que nous avions (un échelon de 5 à 6V) il n'était pas possible de le dériver car c'est un signal discontinu. | ||
| + | |||
| + | C'est pour cela que nous avons choisi de garder une constante pour démarrer et stabiliser le système à une certaine hauteur afin d'éviter les problèmes de données que l'on peut avoir au début de la simulation pour les dix premiers centimètres. | ||
| + | |||
| + | Une fois le niveau stabilisé, nous passons au "Signal Builder" afin d'envoyer un signal sinusoïdal entre 5 et 6V dans le but de remplacer notre échelon, car un signal sinusoïdal est pour sa part dérivable. | ||
| + | On obtient alors le signal d'erreur de chaque cuve dans les 2 scopes "Résidu1" et "Résidu2", comme nous récupérons les signaux "bruts" ils sont bruités, avec un bruit blanc gaussien. | ||
| + | |||
| + | Comme nous commençons à avoir un certain nombre de variables déterminées en lançant un script, afin d'optimiser cette partie là, nous avons copié les lignes de code du fichier .m, directement dans le fichier Simulink dans l'onglet "Model Properties". | ||
| + | |||
| + | Après tout cela terminé, nous avions encore quelques soucis car selon les simulations que nous faisions cela n'était pas toujours cohérent. | ||
| + | On s'est alors rendu compte que lorsque l'on lançait une simulation à 5V pendant 10mn, l'eau ne se stabilisait pas toujours à la même hauteur. | ||
| + | Pour régler ce problème, nous avons ajouté deux blocs dans le sous-système de la boîte noire correspondant aux choix de point de fonctionnement, afin de choisir manuellement la bonne valeur à prendre pour la hauteur des cuves à ce moment là, avant de passer au Signal Builder pour la suite de la simulation. | ||
| + | |||
| + | Notre sous-système du modèle boîte noire ressemble alors maintenant à ceci : | ||
| + | |||
| + | [[File:sous_systeme.png|center|600px|Modèle Boite Noire]] | ||
| + | |||
| + | ==Modèle hors-ligne== | ||
| + | |||
| + | Enfin, afin de finaliser notre projet, nous avons réalisé un script Matlab pour pouvoir effectuer le même traitement que précédemment (modèle d'état + observateur) en chargeant des données préalablement enregistrées grâce au système réel. | ||
| + | On utilise la fonction load() afin de charger les données souhaitées, puis on affecte à des variables, les données dont on aura besoin pour faire le traitement. | ||
| + | |||
| + | On crée deux boucles for afin de "traduire" la soustraction - 5 du signal d'entrée, et le bloc saturation. | ||
| + | Ce qu'il nous faut maintenant, c'est créer le vecteur des sorties pour H1 et H2. Et construire une matrice de données pour ré-estimer le modèle à l'aide de la fonction iddata(). | ||
| + | Avec ces données on va ré-estimer le modèle avec la fonction ssest(). | ||
| + | |||
| + | Pour observer la différence entre la théorie et l'expérimental on compare le modèle estimé avec les mesures. | ||
| + | Ensuite, on extrait les paramètres du modèle d'état de cette estimation, ce qui nous permet de calculer Γ et Γ <sup>t</sup>. | ||
| + | |||
| + | On passe après à la création des défauts sur les 2 sorties avec encore une fois deux boucles for pour chacune des sorties. | ||
| + | Et on finit par le calcul du résidu. Nous avons d'ailleurs également filtrer le signal du résidu car nous avions remarqué avec le système temps réel que celui-ci contenait un bruit blanc gaussien, donc nous avons utilisé un filtre moyenneur qui est en soit un filtre passe bas. | ||
| + | |||
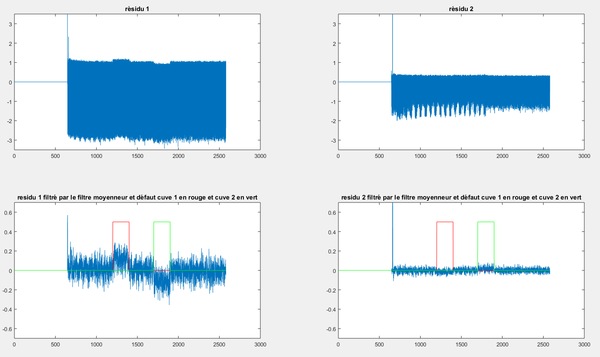
| + | Pour visualiser le tout, nous avons créé 4 figure qui nous intéressait : résidu1, résidu2 et ces même signaux, mais filtrés avec les défauts apparents. | ||
| + | |||
| + | |||
| + | [[File:figure_final.png|center|600px|Figure final]] | ||
=Documents techniques= | =Documents techniques= | ||
| Ligne 326 : | Ligne 626 : | ||
[http://www.pumpagents.com/pdf/ShurfloPumps/2095-212-234.pdf Moteur pompe (équivalent)] <br> | [http://www.pumpagents.com/pdf/ShurfloPumps/2095-212-234.pdf Moteur pompe (équivalent)] <br> | ||
[http://www.ni.com/pdf/manuals/371064f.pdf Boitier permettant de relier la carte d'acquisition avec la commande] <br> | [http://www.ni.com/pdf/manuals/371064f.pdf Boitier permettant de relier la carte d'acquisition avec la commande] <br> | ||
| + | |||
| + | =Fichiers rendus= | ||
| + | |||
| + | Rapport : [[Fichier:Rapport_P60_Vandamme_Villa.pdf ]] | ||
| + | |||
| + | Fichier Simulink + script Matlab : [[Fichier:P60.zip]] | ||
Version actuelle datée du 15 juin 2018 à 21:55
Sommaire
Présentation générale : Commande de niveau d'eau
Objectifs
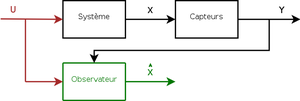
Le principal objectif de ce projet est de créer un observateur, c’est-à-dire reconstruire des valeurs dont on ne dispose pas directement (débit de sortie, niveau d’eau, débit dans le tube reliant les 2 cuves) à partir de valeurs mesurées et de celles dont on dispose, provenant du modèle du système qui sera identifié.
Cet observateur va nous permettre de détecter s’il y a des anomalies (exemple : fuites) dans le système lors d’une simulation grâce à un capteur logiciel. Avec celui-ci nous allons pouvoir d’ailleurs voir la différence des valeurs entre le capteur physique et le capteur logiciel obtenu par l’observateur pour savoir si cela est cohérent. Et pouvoir alors gérer les pannes de capteurs s'il y en a.
Analyse du projet
Positionnement par rapport à l'existant
La mesure d'eau est essentielle pour la collecte de données statistiques et la commande de processus de l'industrie chimique, pétrochimique, et nombreux autres secteurs. Nous analyserons deux concurrents de différents secteurs. Le premier, ERM automatisme industriels, est chargé de la distribution d'eau potable, ils utilisent aussi une système de distribution à base de réservoirs, une pompe et de vannes. Ils utilisent aussi le programme Labview pour la commande et mesures des réservoirs. Ils font des études des systèmes stables et instables en boucle ouverte ou fermée. Nous analyserons juste un système en boucle fermée.
Analyse du premier concurrent : ERM automatisme industriels
- Objectif
Etude des régulations de niveau, débit et pression dans les réservoirs et réseaux d’eau potable: Puisée et rendue potable, l’eau de consommation est généralement transportée vers un ou plusieurs réservoirs situés en hauteur.
- Systeme
Son système doit permettre la distribution d'eau potable en quantité suffisante pour satisfaire les besoins quotidiens des usagers et en même temps répondre à des cas exceptionnels et/ou urgents (lutter contre les incendies). Le niveau des réservoirs, le débit et la pression de l'eau sont par conséquent contrôlés, ajustés et optimisés en permanence.
Régulation et distribution d’eau potable: Le système est constitué dans sa version de base de:
• Réservoir d’eau représentant une réserve d’eau naturelle
• Cuve de stockage d'eau potable
• Transmetteur de niveau analogique (Ultrasons) pour mesure du niveau d'eau dans la cuve
• Pompe à débit variable assurant le remplissage de la cuve
• Un Transmetteur de débit analogique (Effet Vortex)
• Vanne ¼ de tour manuelle permettant de régler le débit d'eau gravitaire en sortie de la cuve
• Electrovanne de perturbation de débit
- Commande
Des exécutables Labview de contrôle commande et mesures sont fournis avec le matériel.
• Analyse fonctionnelle: systèmes de stockage et distribution d’eau potable (SysML fourni)
• Etude des différents principes de mesures (Lois physiques, capteur, transmetteur,...)
• Etude des pompes à débit variable et des vannes
• Identification d’un système stable en BO, en BF (Description des différentes méthodes)
• Régulation et asservissement de niveau simple (P, PI, PD, PID),
• Régulation de niveau intégrateur
• Etude d’un système instable en BO, en BF(Description des différentes méthodes)
• Etude des économies d’énergie dans la gestion d’un réseau d’eau potable
Analyse du second concurrent : L'activité PISCINE
- Objectif
Fondateur d’une société spécialisée dans les installations de sécurité pour les piscines. Le niveau automatique ou remplissage automatique se charge seul de compléter le niveau d’eau d’un bassin, à la suite d’une évaporation, de baignades turbulentes ou d’un lavage de filtre. On l’installe notamment en présence d’un volet automatique immergé.
- Problème
La régulation du niveau d’eau des piscines. Soit ils n’avaient pas pensé, à la construction, à équiper leur bassin d’un système automatique, soit ce système était tombé en panne et ne pouvait être réparé qu’à grands frais. Les solutions qu’ils avaient trouvé n’étaient pas satisfaisantes : jeter un tuyau d’arrosage dans le bassin et attendre de longues minutes, ou faire « biper » une alarme (mais elle ne bipe jamais au bon moment).
Bien pratique, ce dispositif peut toutefois, si l’on n’y prend pas garde et s’il n’est pas équipé d’un dispositif d’alerte détectant un remplissage constant et anormal, masquer une éventuelle fuite. Pièce maîtresse, le robinet flotteur est relié généralement directement au réseau d’eau de la commune avec une simple vanne d’isolement, quand elle existe.
Pour peu qu’il soit défectueux (coincé en position d’ouverture à la suite d’une accumulation de dépôt de calcaire, par exemple), le remplissage ne s’arrête plus. Et si la piscine est pourvue d’un trop-plein, l’apport d’eau neuve risque de s’écouler longtemps avant que l’on ne s’en aperçoive.
- Commande
Risque potentiel de fuite et des quelques contrôles indispensables à connaître afin d’éviter les mauvaises surprises, à savoir :
- un remplissage automatique en action est généralement audible et un bruit d’eau permanent doit alerter l’utilisateur ;
- un niveau d’eau toujours trop haut dans une piscine dépourvue de trop-plein doit lui mettre la puce à l’oreille ;
- une température d’eau qui ne s’élève pas (et pour cause : on remplit à l’eau froide !) est anormale ;
- un traitement d’eau, contrecarré par l’ajout d’eau incessant du réseau qui vient annuler l’effet des corrections, reste inefficace…
Sans ces contrôles, un dysfonctionnement ne peut être détecté
- Solutions
Un moyen simple et efficace pour limiter ces pertes d’eau consiste à raccorder le robinet flotteur à une électrovanne pilotée par une horloge programmée 1 à 2 heures par jour, selon le débit du réseau. Cela permettra de compenser les pertes d’eau normales sans masquer d’éventuelles fuites ou un blocage du robinet flotteur. Un simple programmateur ménager suffirait techniquement pour piloter une électrovanne en 220 V, mais on la choisira impérativement en basse tension 24 V par mesure.
Scénario d'usage du produit ou du concept envisagé
Ce projet peut être mis en place dans les usines utilisant des fluides comme le pétrole, ou encore du liquide explosif. Ce qui peut représenter un grand danger notamment s'il y a des anomalies dans le processus. Il y a donc une nécessité de superviser chaque mesure du système. Mais dans ce cas, que faire lors d'une panne de capteurs ? On va devoir vérifier les cas d’erreurs les plus probables. Pour cela, on va avoir besoin de prévoir la valeur des variables critiques du système et l'associer avec une solution possible selon le problème.
Réponse à la question difficile
Question : Est-ce possible de réaliser un tel projet avec tout type de système (système ouvert, ...) ?
La création d'un observateur est possible pour tout système dynamique avec des mesures de grandeurs connues. Car, en soit un observateur d'état est une extension d'un modèle représenté sous forme de représentation d'état. Lorsque l'état d'un système n'est pas mesurable, on conçoit un observateur qui permet de reconstruire l'état à partir d'un modèle du système dynamique et des mesures d'autres grandeurs.
Préparation du projet
Analyse fonctionnelle
Choix techniques : matériel et logiciel
Pour ce projet, nous allons avoir à disposition le système à 2 réservoirs présent en C008. Celui-ci est composé de deux réservoirs, six vannes, d'un serpentin de retard, d'une pompe et d'un panneau de commande. Ce système est commandé par un ordinateur équipé d’une carte d’acquisition National Instrument, et du noyau Temps Réel dans le logiciel Matlab.
Matlab simulink est un logiciel de modélisation visuelle des systèmes physiques et dynamiques qui peut simuler diverses données avec l'objectif d’assurer que le système marche conformément aux spécifications données et aussi l’optimiser.
Le logiciel a la fonction de réguler le système à cuve en utilisant trois solutions différentes :
- Un correcteur PID
- Une régulation en cascade
- La logique floue
Selon la solution choisie, il trouvera les paramètres du correcteur, présentera la courbe du niveau d’eau en fonction du temps, et corrigera l’erreur du système en sachant les entrées mais sans la connaissance de son modèle mathématique.
Liste des tâches à effectuer
Etape 1 :
Modélisation mathématique du système à l'aide des lois physiques puis estimation des paramètres du modèle à l'aide des données (débit d'entrée et hauteurs mesurées).
Exemple : Si on a modélisé le système et on obtient un deuxième ordre qui est de la forme :
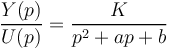 Pour estimer les paramètres du modèle, il faut estimer K, a et b
Pour estimer les paramètres du modèle, il faut estimer K, a et b
Etape 2 :
Conception de l'observateur du système (fait par calcul) et son implémentation sous Matlab Simulink.
Etape 3 :
Génération des signaux indicateurs de défauts appelés résidus à partir des mesures recueillies directement sur le système physique et des données générées par l'observateur
Etape 4 (optionnel) :
Mise en place d'un test statistique pour générer des alarmes
Réalisation du Projet
Feuille d'heures
| Tâche | Prélude | Heures S1 | Heures S2 | Heures S3 | Heures S4 | Heures S5 | Heures S6 | Heures S7 | Heures S8 | Heures S9 | Heures S10 | Heures S11 | Heures S12 | Heures S13 | Heures supp | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Analyse du projet | 8 | 8 | ||||||||||||||
| Travail sur le wiki | 2 | 1 | 1 | 1 | 3 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 6 | 26 | |
| Modélisation sous Simulink | 3 | 2 | 2 | 1 | 0,5 | 8,5 | ||||||||||
| Filtrage du signal + Étalonnage des réservoirs (tension -> cm) | 3 | 2 | 2 | 2 | 2 | 11 | ||||||||||
| Recherche sur les différents éléments du système (principe, datasheet,..) | 2 | 3 | 1 | 2 | 2 | 2 | 1 | 13 | ||||||||
| Simulation sur système réel pour récupérer des données | 2 | 1 | 3 | 2 | 2 | 10 | ||||||||||
| Identification du système : Fonction de transfert, modèle d'état | 1 | 2 | 2 | 2 | 7 | |||||||||||
| Observateur | 1 | 2 | 3 |
Présentation générale du système
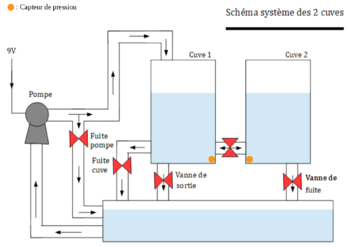
Notre système est composé de 2 cuves, dont la première est remplie en eau par le biais d'une pompe, elle-même alimentée par un moteur dont on choisira la tension par la suite. La pompe est reliée à une grosse cuve qui sert en quelque sorte de réservoir afin de récupérer l'eau qui sera ensuite vidée dans ce même réservoir lorsqu'on ouvre les différentes vannes.
Il y a une sortie principale du système : Vanne de sortie. Le reste des sorties ne simulent que les fuites, comme "Vanne de fuite" et "Fuite cuve". Nous avons également "Fuite pompe", qui génère aussi une fuite. "Fuite pompe" et "Vanne fuite" sont toutes les deux des électrovannes à contrôler par le tableau de commande, alors que "Vanne de fuite" est une vanne manuelle. Il reste une vanne manuelle, qui relie les 2 cuves ensemble, elle peut être fermée si on ne veut remplir que la première cuve (pour travailler sur un premier ordre) ou ouverte pour remplir les deux cuves.
Le système dispose également de deux capteurs de pression (un dans chaque cuve) permettant d'avoir des données afin de connaître le niveau d'eau de chaque cuve. Ces données seront en volts, il faudra donc trouver un moyen pour avoir un niveau d'eau en cm et non en volts.
Principes des éléments du système
- Carte d'acquisition PCI 6024-E
Le système utilise la carte d'acquisition de données de la série NI SC-2345 de National Instruments. La carte prend la mesure à haute tension à partir de capteurs (dans notre cas Pressure Transmitters P28) avec le conditionnement des signaux du NI SCC. Elle arrive à obtenir un taux d'échantillonnage jusqu'à 200k éch./s, avec une résolution de 12 bits sur 16 entrées analogiques asymétriques. En fonction de votre disque dur, le débit de transfert en continu de la carte PC 6024 peut atteindre 200k éch./s.
- Serie SC-2345
Le SC-2345 est doté de connecteurs configurables qui accepte des mini-panneaux de connexion d'E/S, pour une connectivité directe aux signaux/capteurs. Ces boîtiers pour modules de conditionnement de signaux SCC se connectent directement aux matériels d'acquisition de données. Sa fonction est de conditionner des signaux analogiques et numériques de notre dispositif d'acquisition de données (PCI 6024-E)
- MATLAB
En utilisant les matériels NI, nous avons en main un système d'exploitation, un environnement de développement d'application et un choix d'applications logicielles souples. On utilise alors le logiciel MATLAB pour développer le système pour les applications de test, de mesure et de contrôle/commande, qui permet d’accéder rapidement au matériel et aux informations sur les données et on peut afficher les signaux d'E/S. Une interface en ligne de commande, qui est un des éléments du bureau MATLAB, nous permet d’exécuter des commandes simples. Des séquences de commandes peuvent être sauvegardés dans un fichier texte, sous la forme d’un « script » ou encapsulées dans une fonction pour obtenir des calculs.
Par exemple, les calculs du filtre PB :
- Capteurs de niveau des cuves
Le système utilise un capteur de niveau d'eau de type "Transmetteur de pression PCE-28" pour chaque cuve. Ce capteur est capable de mesurer la pression, sous-pression et pression absolue d'un liquide et donner une sortie analogique.
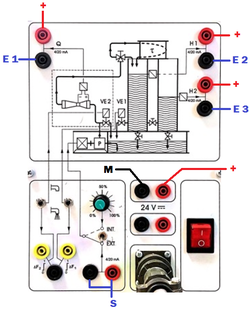
- Câblage des capteurs aux entrées du panneau de commande (SC-2345)
- Relier les bornes "+" des entrées à l'alimentation 24Vcc
- Relier le capteur H1 à l'entrée E2 (ach3)
- Relier le capteur H2 à l'entrée E3 (ach9)
- Relier la borne du signal d'entrée du système à l'entrée E1 (ach0)
- Relier l'entrée S au débit que la pompe doit fournir (DAC0)
Sur le logiciel Matlab les entrées commencent à partir de 1, contrairement au SC-2345 qui commence en 0. Si on veut alors retrouver le numéro de channel attribué aux entrées/sorties, on notera leur numéro +1. Ici, le capteur H1 se trouvera alors en channel 4 et le capteur H2 en channel 10.
Modélisation sous Simulink
Notre premier objectif était d'abord de se familiariser avec le logiciel Matlab en lien avec la maquette des 2 cuves via la carte d'acquisition 6024E intégrée dans la tour d'ordinateur et connectée à la commande qui permet de gérer le système.
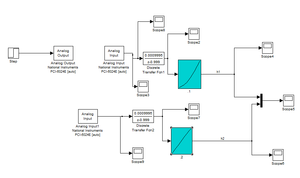
Pour commencer, afin de créer le modèle sous Simulink, il nous fallait savoir comment était contrôlée la pompe du système pour faire parvenir l'eau jusqu'aux cuves. Après quelques observations, nous constatons que la pompe est commandée par un moteur situé à l'intérieur du système. Pour faire démarrer le moteur, il nous faut donc lui envoyer une certaine tension. Sous Simulink, pour envoyer une tension, nous plaçons un bloc step, qui correspond à un signal de X Volts que nous avons à définir. Nous avons alors donné une valeur de 5V arbitrairement, qui pourra être modifiée par la suite mais qui pour l'instant est suffisante pour faire tourner le moteur qui déclenche la pompe et nous permet de remplir les cuves d'eau.
Pour envoyer cette tension au moteur du système on utilise le bloc "Analog Output" (car c'est une valeur qu'on envoie) en paramétrant le numéro de channel sur 1 car l'entrée de la pompe est câblée sur ACH0 (expliqué dans la partie précédente). La tension est alors envoyée via le boitier SC-2345, ce qui permet d'alimenter le moteur, et donc de démarrer la pompe qui va pouvoir remplir une ou deux cuve(s) avec un certain débit.
Ensuite, ce que l'on veut récupérer comme données pour l'instant c'est le niveau d'eau de chaque cuve. Pour récupérer ces valeurs, on regarde où sont câblées les sorties de chacun des capteurs. On note que le capteur pour la première cuve est câblé sur ACH3, et le capteur de la seconde cuve est câblé sur ACH9. On va alors placer 2 blocs "Analog Input" (car on reçoit des données) sur Simulink, un avec comme numéro de channel 4 (1ère cuve) et un avec un numéro de channel 10 (2ème cuve). On place alors dans un premier temps un scope à chaque sortie pour visualiser les signaux de chaque capteur. On remarque alors que nos signaux sont très bruités et qu'ils ont une valeur qui ne correspond pas du tout à une mesure de niveau en cm (ce qui est normal vu qu'on a des capteurs de pression). Pour avoir un signal correct à étudier, on va filtrer le signal afin de réduire un maximum le bruit. Pour cela, on va ajouter le bloc "Discrete Transfer", qui prend en paramètre les coefficients du numérateur et du dénominateur de la fonction de transfert. La démarche de cette méthode sera expliquée dans une prochaine partie.
On a désormais un signal filtré mais nous avons toujours des valeurs qui ne correspondent pas à une mesure en cm. Il va falloir, pour résoudre ce problème, étalonner notre signal. On place alors un bloc "Function Block Parameters", qui utilise la méthode d'interpolation pour réaliser notre étalonnage. On va alors affecter à chaque 5 cm, la valeur que l'on reçoit du capteur. Ceci sera également expliqué dans la prochaine partie plus en détails.
On aura alors en sortie de chaque capteurs (après avoir passé chaque bloc) un signal qui correspond au niveau d'eau en cm, de chaque cuve en temps réel.
Maintenant que ceci est fait, nous avons créé un sous système qui regroupe les blocs de filtrage et d'étalonnage du système afin que cela soit plus épuré dans notre système final.
Filtrage du signal et étalonnage
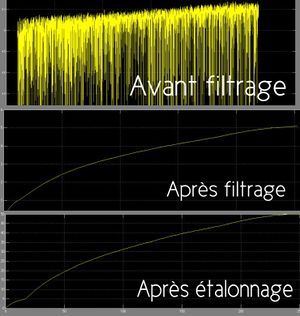
Pour résoudre le problème du bruit sur le signal de sortie, nous avons d'abord réglé la fonction de transfert de notre filtre pour diminuer le bruit avec une valeur de gain obtenue à l'aide des fonctions tf et c2d (conversion d'un système de temps continu à temps discret) de MATLAB.
Nous avons par la suite ajouté l'étalonnage, sa fonction est de donner une relation de valeurs entre la tension reçue et la hauteur en cm du réservoir. Car les capteurs de pression du niveau d’eau mesurent seulement une tension. Ainsi, pour trouver les valeurs à mettre dans notre bloc pour l'étalonnage, une personne a visualisé la hauteur de l'eau tous les 5cm de chaque cuve, tandis que la deuxième a noté les valeurs correspondantes en tension indiquées grâce au scope placé sur notre système Simulink.
Lors de la phase d'étalonnage, il faut que les vannes restent dans la même position, par conséquent nos résultats étaient faux lors de notre première mesure et nous avons du réitérer cette opération. Car nous avions fait l'étalonnage sur le premier réservoir en fermant la vanne reliant les 2 cuves, puis nous avions ouvert celle ci pour réaliser l'étalonnage sur le second réservoir et de ce fait cela modifiait les résultats obtenus sur le premier réservoir.
De plus, notre tuteur nous a demandé de recalibrer notre signal d'entrée du système qui correspond à une tension envoyée au moteur qui commande la pompe, en regardant au niveau du signal de sortie sur le scope à partir de quelle tension la courbe devient linéaire, et ensuite ajuster le signal d'entrée en fonction de ceci.
De ce fait, nous avons choisi un signal d'entrée de 9V afin d'être dans la partie linéaire de la pompe et d'avoir un débit suffisant au niveau de la pompe pour réaliser un étalonnage correct en ayant la vanne de sortie ouverte et le remplissage des 2 cuves entièrement.
Fonction de transfert du système
En regardant les signaux des deux capteurs de niveau d’eau, avec notre tuteur, nous avons conclu que le système a un comportement non linéaire pour une tension d'entrée à 3 volts. De ce fait, pour la suite du projet, nous allons ignorer cette plage de valeurs (0 à 3V) en entrée. Le capteur de pression servant pour les niveaux d'eau ne sont pas précis. En effet, si nous augmentons le signal d’entrée entre 0 et 9 volts, le débit de la pompe change et par conséquent, la pression varie et ne donne pas en temps réel le bon résultat. Il y a toujours un laps de temps pour que cela se stabilise un minimum.
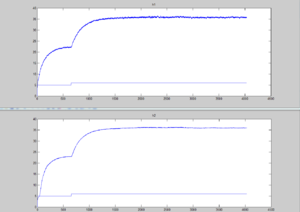
Nous identifions alors notre système de deux cuves comme système du deuxième ordre. Les équations différentielles linéaires de deuxième ordre et de coefficients constants, décrivent la dynamique d’un système qui à l’intérieur a deux éléments de stockage d'énergie, dans notre cas, il s'agit des deux réservoirs d’eau. Nous avons fait une simulation avec une signal d’entrée de 5 volts pendant 10 minutes et à 6 volts pendant 56 minutes et nous avons obtenu un signal pour chaque cuve de la hauteur par rapport au temps.
On décrira notre système linéaire du second ordre avec le modèle mathématique, il aura une fonction de transfert sous la forme suivante :
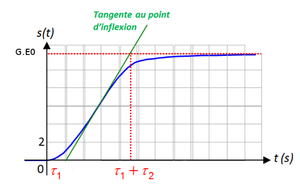
Nous avons choisi les valeurs de la fonction, en tenant compte de la courbe de la cuve 1 à 6 volts. Le gain (K) est la différence entre la hauteur maximale et minimale, c'est à dire 35,5-21,5=14. Pour les valeurs des τn nous avons tracé une tangente au point d'inflexion de cette courbe. La tangente à t=0 est horizontale et la tangente au point d'inflexion de la courbe coupe l'axe des abscisses en τ1 et l'asymptote de la valeur finale en τ1+τ2. Le point d'inflexion sera à 63% du le gain (14*0,63=8,82) et τ sera égal au point sur l'intersection de l'axe de temps qui correspond à la hauteur (21,5+8,82).
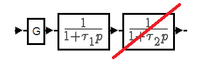
Nous avons mesuré la valeur de τ1 et dans notre cas elle est quasi nulle, donc comme le système est équivalent à deux systèmes du 1er ordre placés en série, il est possible de le simplifier à un système de second ordre.
Finalement la fonction de transfert est:
Modèle d'état
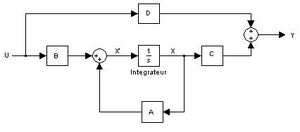
En automatique, une représentation d'état permet de modéliser un système dynamique en utilisant des variables d'état. Cette représentation, qui peut être linéaire ou non, continue ou discrète, permet de déterminer l'état du système à n'importe quel instant futur si l'on connaît l'état à l'instant initial et le comportement des variables exogènes qui influent sur le système. La représentation d'état du système permet de connaître son comportement "interne" et pas seulement son comportement "externe" comme c'est le cas avec sa fonction de transfert.
La représentation d'état de ces systèmes, quand ils sont à temps continu, s'écrit de la manière suivante :
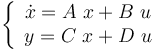
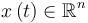 : colonne qui représente les n variables d'état
: colonne qui représente les n variables d'état
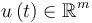 : colonne qui représente les m commandes
: colonne qui représente les m commandes
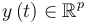 : colonne qui représente les p sorties
: colonne qui représente les p sorties
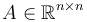 : Matrice d'état
: Matrice d'état
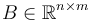 : Matrice de commande
: Matrice de commande
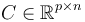 : Matrice d'observation
: Matrice d'observation
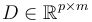 : Matrice d'action directe
: Matrice d'action directe
Dans notre cas, nous allons faire l'identification entre fonction de transfert et modèle d'état pour trouver A, B, C et D.
On a en théorie pour un système du 1er ordre :
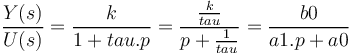
Ce qui nous donne dans notre cas, avec nos fonctions de transfert :
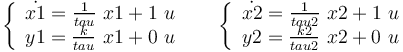
Ceci représente 2 modèles que l'on va rassembler en un.
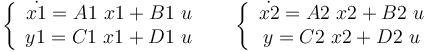
On pose :
On aura alors :
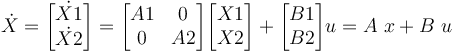
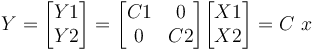
On implémente le modèle d'état que l'on vient de trouver dans notre fichier Simulink, dans le sous-système du modèle boîte noire.
Observateur
Si on veut estimer x et y (vu précédemment dans le modèle d'état), on les construit par la sortie, qui elle même a un défaut. Pour cela, on va utiliser la méthode de l'espace de parité.
On réalise cette méthode à partir des équations présentes dans le modèle d'état, que l'on va dériver n fois (dans la théorie).
- Théorie de la méthode
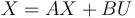
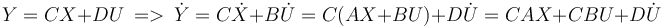
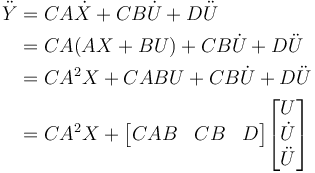
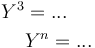
Dans notre cas, on a n=1 car on utilise une équation du premier ordre.
Ce qui nous donne :
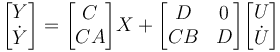
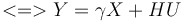
On veut trouver une matrice qui annule Γ en la multipliant.
Pour ce faire, nous allons utiliser le théorème de Cayley Hamilton, et nous nommerons la matrice : Γ t, matrice orthogonale.
Celle-ci sera créée sur Matlab grâce à la fonction null() avec Γ' (" ' " pour la transposée) en paramètre. Cela va nous retourner une matrice contenant des valeurs possibles afin d'annuler la matrice Γ.
Maintenant, l'idée est d'avoir un signal de défaut (que l'on nommera f par la suite) donc en prenant la première ligne de cette matrice on a un vecteur de la base, ce qui est suffisant.
Pour ne récupérer que la première ligne, on procède comme ceci : 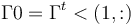
Comme nous avons 2 sorties (H1 et H2), nous allons avoir besoin de 2 défauts. On va, de ce fait récupérer également la deuxième ligne de Γ.
On a alors :
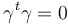
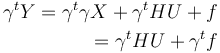
Donc :
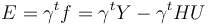
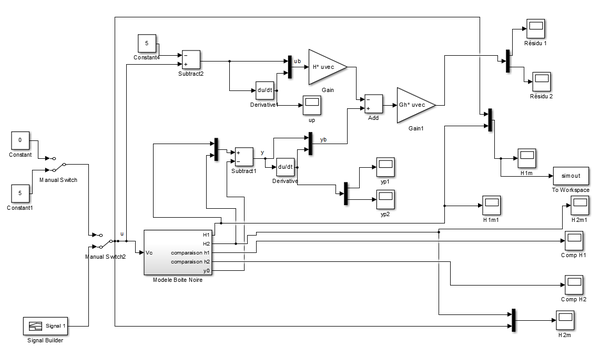
E représentant le "résidu", soit l'erreur qui peut avoir dans le système, généré par exemple par un ou plusieurs fuites. Nous pouvons maintenant implémenter ceci sur notre Simulink.
On soustrait - 5 lorsque l'on récupère U afin de se placer au point de fonctionnement (de redéfinir l'origine en quelque sorte). Nous devons obligatoirement réaliser cela car nous travaillons sur un système de base non linéaire, donc on va se concentrer uniquement sur une partie linéaire, dont l'origine est à 5V. Et on travaillera dans ce voisinage de valeurs.
Pour mettre en place le résidu, nous utilisons des dérivées. Avec le signal d'entrée que nous avions (un échelon de 5 à 6V) il n'était pas possible de le dériver car c'est un signal discontinu.
C'est pour cela que nous avons choisi de garder une constante pour démarrer et stabiliser le système à une certaine hauteur afin d'éviter les problèmes de données que l'on peut avoir au début de la simulation pour les dix premiers centimètres.
Une fois le niveau stabilisé, nous passons au "Signal Builder" afin d'envoyer un signal sinusoïdal entre 5 et 6V dans le but de remplacer notre échelon, car un signal sinusoïdal est pour sa part dérivable. On obtient alors le signal d'erreur de chaque cuve dans les 2 scopes "Résidu1" et "Résidu2", comme nous récupérons les signaux "bruts" ils sont bruités, avec un bruit blanc gaussien.
Comme nous commençons à avoir un certain nombre de variables déterminées en lançant un script, afin d'optimiser cette partie là, nous avons copié les lignes de code du fichier .m, directement dans le fichier Simulink dans l'onglet "Model Properties".
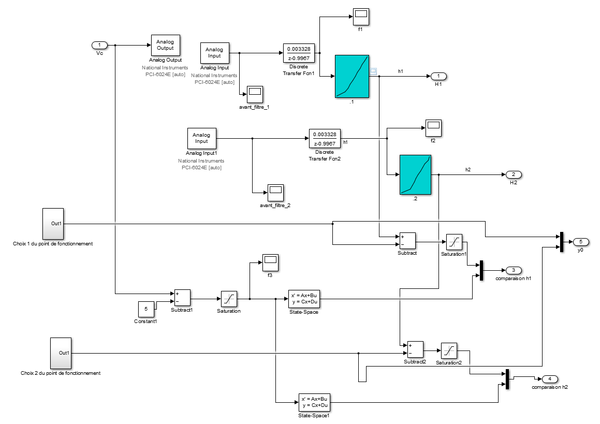
Après tout cela terminé, nous avions encore quelques soucis car selon les simulations que nous faisions cela n'était pas toujours cohérent. On s'est alors rendu compte que lorsque l'on lançait une simulation à 5V pendant 10mn, l'eau ne se stabilisait pas toujours à la même hauteur. Pour régler ce problème, nous avons ajouté deux blocs dans le sous-système de la boîte noire correspondant aux choix de point de fonctionnement, afin de choisir manuellement la bonne valeur à prendre pour la hauteur des cuves à ce moment là, avant de passer au Signal Builder pour la suite de la simulation.
Notre sous-système du modèle boîte noire ressemble alors maintenant à ceci :
Modèle hors-ligne
Enfin, afin de finaliser notre projet, nous avons réalisé un script Matlab pour pouvoir effectuer le même traitement que précédemment (modèle d'état + observateur) en chargeant des données préalablement enregistrées grâce au système réel. On utilise la fonction load() afin de charger les données souhaitées, puis on affecte à des variables, les données dont on aura besoin pour faire le traitement.
On crée deux boucles for afin de "traduire" la soustraction - 5 du signal d'entrée, et le bloc saturation. Ce qu'il nous faut maintenant, c'est créer le vecteur des sorties pour H1 et H2. Et construire une matrice de données pour ré-estimer le modèle à l'aide de la fonction iddata(). Avec ces données on va ré-estimer le modèle avec la fonction ssest().
Pour observer la différence entre la théorie et l'expérimental on compare le modèle estimé avec les mesures. Ensuite, on extrait les paramètres du modèle d'état de cette estimation, ce qui nous permet de calculer Γ et Γ t.
On passe après à la création des défauts sur les 2 sorties avec encore une fois deux boucles for pour chacune des sorties. Et on finit par le calcul du résidu. Nous avons d'ailleurs également filtrer le signal du résidu car nous avions remarqué avec le système temps réel que celui-ci contenait un bruit blanc gaussien, donc nous avons utilisé un filtre moyenneur qui est en soit un filtre passe bas.
Pour visualiser le tout, nous avons créé 4 figure qui nous intéressait : résidu1, résidu2 et ces même signaux, mais filtrés avec les défauts apparents.
Documents techniques
Capteur de pression (niveau d'eau)
Vannes électriques "PD type" (pompe et cuve)
Moteur pompe (équivalent)
Boitier permettant de relier la carte d'acquisition avec la commande
Fichiers rendus
Rapport : Fichier:Rapport P60 Vandamme Villa.pdf
Fichier Simulink + script Matlab : Fichier:P60.zip